Комплексный многогранник

Комплексный многогранник — это обобщение многогранника в Шаблон:Не переведено 5 на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.

Комплексный многогранник можно понимать как коллекцию комплексных точек, прямых, плоскостей и так далее, где в каждой точке пересекаются несколько прямых, в каждой прямой несколько плоскостей и т. д.

Точное определение существует только для правильных комплексных многогранников, которые являются конфигурациями. Правильные комплексные многогранники полностью описаны и могут быть описаны с помощью символической нотации, разработанной Коксетером.

Описаны также некоторые комплексные многогранники, не являющиеся правильными.

Определение и вводные замечания

Комплексная прямая $ℂ^{1}$ имеет одну размерность с вещественными координатами и другую с мнимыми координатами. Если использованы вещественные координаты для обоих размерностей, говорят о задании двух размерностей над вещественными числами. Вещественная плоскость с мнимой осью называется диаграммой Аргана. Ввиду этого она называется иногда комплексной плоскостью. Комплексное 2-пространство (которое иногда также называется комплексной плоскостью) тогда является четырёхмерным пространством над вещественными числами.

Комплексный n-многогранник в комплексном n-пространстве аналогичен вещественному n-многограннику в вещественном n-пространстве.

Нет естественного комплексного аналога порядку точки на вещественной оси (или связанных комбинаторных свойств). Вследствие этого комплексный многогранник нельзя рассматривать как непрерывную поверхность и он не ограничивает внутренность, как это происходит в вещественном случае.

В случае правильных многогранников точное определение можно дать с помощью понятия симметрии. Для любого правильного многогранника группа симметрии (здесь, группа комплексных отражений, называемая группой Шепарда) действует транзитивно на флагах, то есть на вложенные наборы точек, содержащихся в прямых, которые принадлежат плоскости и так далее.

Более полно, говорят, что набор P аффинных подпространств (или плоскостей) комплексного унитарного пространства V размерности n является правильным комплексным многогранником, если он удовлетворяет следующим условиямШаблон:Sfn Шаблон:Sfn:

для любых $- 1 ⩽ i < j < k ⩽ n$ , если Шаблон:Math является плоскостью в P размерности i и Шаблон:Math является плоскостью в P размерности k, такие, что $F \subset H$ , то существует по меньшей мере две плоскости G в P размерности j такие, что $F \subset G \subset H$ ;
для любых Шаблон:Math, таких что $- 1 ⩽ i < j - 2, j ⩽ n$ , если $F \subset G$ являются плоскостями пространства P размерностей i, j, то множество плоскостей между F и G связно, в том смысле, что можно получить из любого члена этого множества любой другой как последовательность вложений
подмножество унитарных преобразований V, не изменяющих P, транзитивно на флагах $F_{0} \subset F_{1} \subset \dots \subset F_{n}$ плоскостей P (с $F_{i}$ размерности i для всех i) (Здесь под плоскостью размерности −1 понимается пустое множество). Таким образом, по определению, правильные комплексные многогранники — это конфигурации в комплексном пространстве.

Правильные комплексные многогранники были открыты Шаблон:Не переведено 5 (1952) и их теория была позднее развита Коксетером (1974).

Три взгляда на *правильные комплексные многоугольники* $_{4} {4}_{2}$ , Шаблон:CDD
Этот комплексный многоугольник имеет 8 рёбер (комплексные прямые) с метками a..h и 16 вершин. Четыре вершины лежат на каждом ребре и в каждой вершине пересекаются два ребра. На левом рисунке квадраты не являются элементами многогранника, но нарисованы исключительно помочь распознать вершины, лежащие на той же самой комплексной прямой. Восьмиугольный периметр левого изображения не является элементом многогранника, но он является многоугольником Петри^[1]. На центральном рисунке каждое ребро представлено как вещественная прямая и четыре вершины на каждой прямой можно легко видеть.	Эскиз в перспективе, представляющий 16 вершин в виде чёрных точек и 8 4-рёбер как квадраты внутри каждого ребра. Зелёный путь представляет восьмиугольный периметр левого изображения.

Комплексный многогранник существует в комплексном пространстве эквивалентной размерности. Например, вершины комплексного многоугольника — это точки на комплексной плоскости $ℂ^{2}$ , а рёбра — комплексные прямые $ℂ^{1}$ , существующие как (аффинные) подпространства плоскости, пересекающиеся в вершинах. Таким образом, ребро может быть задано одним комплексным числом.

В правильном комплексном многограннике вершины, инцидентные ребру, располагаются симметрично относительно барицентра, который часто используется как начало координатной системы ребра (в вещественном случае барицентром является просто середина ребра). Симметрия возникает из комплексных отражений относительно барицентра. Это отражение оставляет модуль любой вершины неизменным, но меняет её аргумент на постоянную величину, передвигая её в координаты следующей по порядку вершины. Таким образом, мы можем считать (после подходящего выбора шкалы), что вершины ребра удовлетворяют уравнению $x^{p} - 1 = 0$ , где p — число инцидентных вершин. Таким образом, на диаграмме Аргана ребра, точки вершины лежат в вершинах правильного многоугольника с центром в начале координат.

Выше проиллюстрированы три вещественные проекции правильного комплексного многоугольника 4{4}2 с рёбрами a, b, c, d, e, f, g, h. Многоугольник имеет 16 вершин, которые для удобства обзора индивидуально не помечены. Каждое ребро имеет четыре вершины, а каждая вершина лежит на двух рёбрах, поскольку каждое ребро пересекает четыре других ребра. На первой диаграмме каждое ребро представлено квадратом. Стороны квадрата не являются частями многоугольника, но нарисованы исключительно для облегчения визуальных связей четырёх вершин. Рёбра располагаются симметрично. (Заметьте, что диаграмма выглядит подобно B₄ плоской проекции Коксетера тессеракта, но структурно она другая).

На средней диаграмме не соблюдается восьмиугольная симметрия в пользу ясности. Каждое ребро показано как вещественная прямая, а каждая точка пересечения двух прямых является вершиной. Связь между различными рёбрами легко видеть.

Последняя диаграмма показывает структуру, спроецированную в трёхмерное пространство — два куба вершин, фактически, имеют один и тот же размер, но рассматриваются в перспективе с различного расстояния в четырёхмерном пространстве.

Правильные комплексные одномерные многогранники

Вещественный 1-мерный многогранник существует как замкнутый отрезок на вещественной прямой $ℝ^{1}$ , определяемый двумя концами или вершинами. Его символом Шлефли — {} .

Аналогично, комплексный 1-многогранник существует как множество p из вершин на комплексной прямой $ℂ^{1}$ . Они могут быть представлены как множество точек на диаграмме Аргана (x,y)=x+iy. Правильный комплексный 1-мерный многогранник _p{} имеет p (p ≥ 2) вершин, расположенных в виде выпуклого правильного многоугольника {p} на комплексной плоскостиШаблон:Sfn.

В отличие от точек на вещественной прямой, точки на комплексной прямой не имеют естественного упорядочения. Тогда, в отличие от вещественных многогранников, нельзя определить никакой внутренности^[2]. Вопреки этому, комплексные 1-многогранники часто рисуют, как здесь, в виде ограниченных правильных многоугольник на комплексной плоскости.

Реальные рёбра генерируются как отрезки между точками и их отражениями в зеркале. Комплексное отражение порядка 2 можно рассматривать как вращение на 180 градусов вокруг центра. Ребро *неактивно*, если генераторная точка находится на линии зеркала или в центре.

Правильный вещественный 1-мерный многогранник представляется пустым символом Шлефли {} или диаграммой Коксетера — Дынкина Шаблон:CDD. Точка или узел диаграммы Коксетера — Дынкина представляет генератор отражения, в то время как кружок вокруг узла означает, что точка генератора не находится на зеркале, так что её зеркальное отражение отличается от самой точки. Согласно расширенной нотации правильный комплексный 1-мерный многогранник в $ℂ^{1}$ , содержащий p вершин, имеет диаграмму Коксетера — Дынкина Шаблон:CDD для любого положительного целого p (большего или равного 2). Число p можно опустить, если оно равно 2. Этот многогранник может быть также представлен пустым символом Шлефли $_{p} {},}_{p} {, {}_{p}$ или $_{p} {2}_{1}$ . 1 — это заполнитель, представляющий несуществующее отражение или тождественный генератор с периодом 1. (0-многогранник, вещественный или комплексный — это точка и представляется как } {, или как $_{1} {2}_{1}$ .)

Симметрия обозначается диаграммой Коксетера Шаблон:CDD и может быть альтернативно описана Шаблон:Не переведено 5 как $_{p} [], []_{p}$ , или $]_{p} [,_{p} [2]_{1}$ , или $_{p} [1]_{p}$ . Симметрия изоморфна циклической группе, порядка pШаблон:Sfn. Подгруппами $_{p} []$ являются любые полные делители $d,_{d} []$ , где $d ⩾ 2$ .

Генератор унитарного оператора для Шаблон:CDD выглядит как вращение на 2π/p радиан по часовой стрелке, а Шаблон:CDD ребро образуется последовательным применением одного комплексного отражения. Генератор комплексного отражения для 1-многогранника с p вершинами — это $e^{2 π i / p} = \cos (2 π / p) + i \sin (2 π / p)$ . Если p = 2, генератором будет $e^{π i} = - 1$ , то же, что и центральная симметрия на вещественной плоскости.

В комплексных многогранниках большей размерности 1-многогранники образуют p-рёбра. 2-ребро подобно обычному вещественному ребру, поскольку содержит две вершины, но не обязательно существует на вещественной прямой.

Правильные комплексные многоугольники

Хотя 1-многогранники могут иметь неограниченную величину p, конечные правильные комплексные многоугольники, за исключением многоугольников двойных призм $_{p} {4}_{2}$ , ограничены 5-рёбрами (пятиугольные рёбра), а бесконечные правильные апейрогоны включают также 6-рёбра (шестиугольные рёбра).

Обозначения

Модифицированные Шепардом обозначения Шлефли

Шаблон:Не переведено 5 первоначально придумал модифицированную форму нотации Шлефли для правильных многогранников. Для многоугольника, ограниченного p₁-рёбрами, с p₂-множествами в качестве вершинных фигур и общей группой симметрии порядка g, мы обозначаем многоугольник как $p_{1} (g) p_{2}$ .

Число вершин V тогда равно $g / p_{2}$ , а число рёбер E равно $g / p_{1}$ .

Комплексный многоугольник, проиллюстрированный выше, имеет восемь квадратных рёбер ( $p_{1} = 4$ ) и шестнадцать вершин ( $p_{2} = 2$ ). Отсюда мы можем заключить, что g = 32, что даёт модифицированный символ Шлефли 4(32)2.

Пересмотренная нотация Шлефли

Более современная нотация $_{p_{1}} {q}_{p_{2}}$ принадлежит Коксетеру Шаблон:Sfn и основывается на теории групп. Символом группы симметрии будет $_{p_{1}} [q]_{p_{2}}$ .

Группа симметрии $_{p_{1}} [q]_{p_{2}}$ представлена двумя генераторами $R_{1}, R_{2}$ , где: $R_{1}^{p_{1}} = R_{2}^{p_{2}} = I$ . Если q чётно, $(R_{2} R_{1})^{q / 2} = (R_{1} R_{2})^{q / 2}$ . Если q нечётно, $(R_{2} R_{1})^{(q - 1) / 2} R_{2} = (R_{1} R_{2})^{(q - 1) / 2} R_{1}$ . Когда q нечётно, $p_{1} = p_{2}$ .

Для $_{4} [4]_{2}$ имеет место $R_{1}^{4} = R_{2}^{2} = I$ , $(R_{2} R_{1})^{2} = (R_{1} R_{2})^{2}$ .

Для $_{3} [5]_{3}$ имеет место $R_{1}^{3} = R_{2}^{3} = I$ , $(R_{2} R_{1})^{2} R_{2} = (R_{1} R_{2})^{2} R_{1}$ .

Диаграммы Коксетера — Дынкина

Коксетер также обобщил использование диаграмм Коксетера — Дынкина на комплексные многогранники. Например, комплексный многоугольник $_{p} {q}_{r}$ представляется диаграммой Шаблон:CDD, а эквивалентная группа симметрии $_{p} [q]_{r}$ представляется диаграммой без кружка Шаблон:CDD. Узлы p и r представляют зеркала, дающие образы p и r на плоскости. Непомеченные узлы на диаграмме имеют 2 неявные метки. Например, вещественный правильный многоугольник имеет обозначение $_{2} {q}_{2}$ , или {q}, или Шаблон:CDD.

Подгруппы $_{p} [4]_{2}$ : p=2,3,4…
$_{p} [4]_{2} \to [p]$ , индекс p
$_{p} [4]_{2} \to_{p} [] \times_{p} []$ , индекс 2

Имеется ограничение: узлы, связанные нечётными порядками ветвления, должны иметь идентичные порядки узлов. Если это не так, группа создаст «звёздчатые» многогранники с накладывающимися элементами. Таким образом, Шаблон:CDD и Шаблон:CDD являются обычными многоугольниками, в то время как Шаблон:CDD является звёздчатым.

Перечисление правильных многоугольников

Коксетер привёл список правильных комплексных многоугольников в $ℂ^{2}$ . Правильный комплексный многоугольник, $_{p} {q}_{r}$ или Шаблон:CDD, имеет p-рёбер и q-угольные вершинные фигуры. $_{p} {q}_{r}$ является конечным многогранником, если $(p + r) q > p r (q - 2)$ .

Симметрия правильного многоугольника, записываемая как $_{p} [q]_{r}$ , называется группа Шепарда, по аналогии с группой Коксетера, позволяя как вещественные, так и комплексные отражения.

Для незвёздчатых групп порядок группы $_{p} [q]_{r}$ можно вычислить как $g = 8 / q \cdot (1 / p + 2 / q + 1 / r - 1)^{- 2}$ Шаблон:Sfn.

Число Коксетера для $_{p} [q]_{r}$ равно $h = 2 / (1 / p + 2 / q + 1 / r - 1)$ , так что порядок группы может быть также вычислен как $g = 2 h^{2} / q$ . Правильный комплексный многочлен можно нарисовать в ортогональной проекции с h-гональной симметрией.

Решения ранга 2 генерируют следующие комплексные многоугольники:

Группа	$G_{3} = G (q, 1, 1)$	$G_{2} = G (p, 1, 2)$	$G_{4}$	$G_{6}$	G₅	G₈	G₁₄	G₉	G₁₀	G₂₀	G₁₆	G₂₁	G₁₇	G₁₈
	$_{2} [q]_{2}$ , q=3,4…	$_{p} [4]_{2}$ , p=2,3…	$_{3} [3]_{3}$	$_{3} [6]_{2}$	$_{3} [4]_{3}$	$_{4} [3]_{4}$	$_{3} [8]_{2}$	$_{4} [6]_{2}$	$_{4} [4]_{3}$	$_{3} [5]_{3}$	$_{5} [3]_{5}$	$_{3} [10]_{2}$	$_{5} [6]_{2}$	$_{5} [4]_{3}$
	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD
Порядок	2q	2p²	24	48	72	96	144	192	288	360	600	720	1200	1800

Исключены решения с нечётными q и неравными p и r: $_{6} [3]_{2},_{6} [3]_{3},_{9} [3]_{3},_{1} 2 [3]_{3}, \dots,_{5} [5]_{2},_{6} [5]_{2},_{8} [5]_{2},_{9} [5]_{2},_{4} [7]_{2},_{9} [5]_{2},_{3} [9]_{2}$ , и $_{3} [11]_{2}$ .

Другие целые q с неравными p и r, создают звёздчатые группы с перекрывающимися фундаментальными областями: Шаблон:CDD, Шаблон:CDD, Шаблон:CDD, Шаблон:CDD, Шаблон:CDD, и Шаблон:CDD.

Двойственный многоугольник для многоугольника $_{p} {q}_{r}$ — это $_{r} {q}_{p}$ . Многоугольник вида $_{p} {q}_{p}$ самодвойственен. Группы вида $_{p} [2 q]_{2}$ имеют половинную симметрию $_{p} [q]_{p}$ , так что правильный многоугольник Шаблон:CDD является тем же, что и квазиправильный Шаблон:CDD. Также правильный многоугольник с теми же порядками узлов, Шаблон:CDD, имеет Шаблон:Не переведено 5 построение Шаблон:CDD, позволяющее смежным рёбрам иметь два различных цветаШаблон:Sfn.

Порядок группы, g, используется для вычисления полного числа вершин и рёбер. Многогранник имеет g/r вершин и g/p рёбер. Если p=r, число вершин и рёбер равно. Это условие необходимо, если q нечётно.

Группа	Порядок	Число Коксетера	Многоугольник		Вершины	Рёбра		Примечания
G(q, q,2) $_{2} [q]_{2} = [q]$ q=2,3,4,…	2q	q	$_{2} {q}_{2}$	Шаблон:CDD	q	q	{}	Вещественные правильные многоугольники То же, что и Шаблон:CDD То же, что и Шаблон:CDD, если q чётно

Группа	Порядок	Число Коксетера	Многогранник			Вершины	Рёбра		Примечания
G(p,1,2) $_{p} [4]_{2}$ p=2,3,4,…	2p²	2p	$p (2 p^{2}) 2$	$_{p} {4}_{2}$	Шаблон:CDD	$p^{2}$	2p	$_{p} {}$	то же, что и $_{p} {} \times_{p} {}$ или Шаблон:CDD $ℝ^{4}$ представление как p-p дуопризма
G(p,1,2) $_{p} [4]_{2}$ p=2,3,4,…	2p²	2p	2(2p²)p	$_{2} {4}_{p}$	Шаблон:CDD	2p	$p^{2}$	{}	$ℝ^{4}$ представление как p-p Шаблон:Не переведено 5
G(2,1,2) $_{2} [4]_{2} = [4]$	8	4		$_{2} {4}_{2} = {4}$	Шаблон:CDD	4	4	{}	то же, что и {}×{} или Шаблон:CDD Вещественный квадрат
G(3,1,2) $_{3} [4]_{2}$	18	6	6(18)2	$_{3} {4}_{2}$	Шаблон:CDD	9	6	$_{3} {}$	то же, что и $_{3} {} \times_{3} {}$ или Шаблон:CDD $ℝ^{4}$ представление как 3-3 дуопризма
G(3,1,2) $_{3} [4]_{2}$	18	6	2(18)3	$_{2} {4}_{3}$	Шаблон:CDD	6	9	{}	$ℝ^{4}$ представление как 3-3 дуопризма
G(4,1,2) $_{4} [4]_{2}$	32	8	8(32)2	$_{4} {4}_{2}$	Шаблон:CDD	16	8	$_{4} {}$	то же, что и $_{4} {} \times_{4} {}$ или Шаблон:CDD $ℝ^{4}$ представление в виде 4-4 дуопризмы или {4,3,3}
G(4,1,2) $_{4} [4]_{2}$	32	8	2(32)4	$_{2} {4}_{4}$	Шаблон:CDD	8	16	{}	$ℝ^{4}$ представление в виде 4-4 дуопризмы или {3,3,4}
G(5,1,2) $_{5} [4]_{2}$	50	25	5(50)2	$_{5} {4}_{2}$	Шаблон:CDD	25	10	$_{5} {}$	то же, что и $_{5} {} \times_{5} {}$ или Шаблон:CDD $ℝ^{4}$ представление как 5,5-дуопризма
G(5,1,2) $_{5} [4]_{2}$	50	25	2(50)5	$_{2} {4}_{5}$	Шаблон:CDD	10	25	{}	$ℝ^{4}$ представление как Шаблон:Не переведено 5
G(6,1,2) $_{6} [4]_{2}$	72	36	6(72)2	₆{4}₂	Шаблон:CDD	36	12	$_{6} {}$	то же, что и $_{6} {} \times_{6} {}$ или Шаблон:CDD $ℝ^{4}$ представление как Шаблон:Не переведено 5
G(6,1,2) $_{6} [4]_{2}$	72	36	2(72)6	$_{2} {4}_{6}$	Шаблон:CDD	12	36	{}	$ℝ^{4}$ представление как Шаблон:Не переведено 5
$G_{4} = G (1, 1, 2)$ ₃[3]₃ <2,3,3>	24	6	3(24)3	Шаблон:Не переведено 5	Шаблон:CDD	8	8	$_{3} {}$	Конфигурация Мёбиуса — Кантора самодвойственный, то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,3,4}
$G_{6}$ $_{3} [6]_{2}$	48	12	3(48)2	$_{3} {6}_{2}$	Шаблон:CDD	24	16	₃{}	то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,4,3}
				$_{3} {3}_{2}$	Шаблон:CDD	24	16	₃{}	звёздчатый многоугольник
			2(48)3	$_{2} {6}_{3}$	Шаблон:CDD	16	24	{}	$ℝ^{4}$ представление как {4,3,3}
				$_{2} {3}_{3}$	Шаблон:CDD	16	24	{}	звёздчатый многоугольник
G₅ ₃[4]₃	72	12	3(72)3	$_{3} {4}_{3}$	Шаблон:CDD	24	24	₃{}	самодвойственный, то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,4,3}
G₈ ₄[3]₄	96	12	4(96)4	₄{3}₄	Шаблон:CDD	24	24	₄{}	самодвойственный, то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,4,3}
G₁₄ $_{3} [8]_{2}$	144	24	3(144)2	$_{3} {8}_{2}$	Шаблон:CDD	72	48	₃{}	то же, что и Шаблон:CDD
				₃{8/3}₂	Шаблон:CDD	72	48	₃{}	звёздчатый многоугольник, то же, что и Шаблон:CDD
			2(144)3	₂{8}₃	Шаблон:CDD	48	72	{}
				₂{8/3}₃	Шаблон:CDD	48	72	{}	звёздчатый многоугольник
G₉ ₄[6]₂	192	24	4(192)2	₄{6}₂	Шаблон:CDD	96	48	₄{}	то же, что и Шаблон:CDD
			2(192)4	₂{6}₄	Шаблон:CDD	48	96	{}
				₄{3}₂	Шаблон:CDD	96	48	{}	звёздчатый многоугольник
				₂{3}₄	Шаблон:CDD	48	96	{}	звёздчатый многоугольник
G₁₀ ₄[4]₃	288	24	4(288)3	₄{4}₃	Шаблон:CDD	96	72	₄{}
		12		₄{8/3}₃	Шаблон:CDD	96	72	₄{}	звёздчатый многоугольник
		24	3(288)4	₃{4}₄	Шаблон:CDD	72	96	₃{}
		12		₃{8/3}₄	Шаблон:CDD	72	96	₃{}	звёздчатый многоугольник
G₂₀ ₃[5]₃	360	30	3(360)3	₃{5}₃	Шаблон:CDD	120	120	₃{}	самодвойственный, то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,3,5}
G₂₀ ₃[5]₃	360	30		₃{5/2}₃	Шаблон:CDD	120	120	₃{}	самодвойственный, звёздчатый многоугольник
G₁₆ ₅[3]₅	600	30	5(600)5	₅{3}₅	Шаблон:CDD	120	120	₅{}	самодвойственный, то же, что и Шаблон:CDD $ℝ^{4}$ представление как {3,3,5}
G₁₆ ₅[3]₅	600	10		₅{5/2}₅	Шаблон:CDD	120	120	₅{}	самодвойственный, звёздчатый многоугольник
G₂₁ ₃[10]₂	720	60	3(720)2	₃{10}₂	Шаблон:CDD	360	240	₃{}	то же, что и Шаблон:CDD
				₃{5}₂	Шаблон:CDD				звёздчатый многоугольник
				₃{10/3}₂	Шаблон:CDD				звёздчатый многоугольник, то же, что и Шаблон:CDD
				₃{5/2}₂	Шаблон:CDD				звёздчатый многоугольник
			2(720)3	₂{10}₃	Шаблон:CDD	240	360	{}
				₂{5}₃	Шаблон:CDD				звёздчатый многоугольник
				₂{10/3}₃	Шаблон:CDD				звёздчатый многоугольник
				₂{5/2}₃	Шаблон:CDD				звёздчатый многоугольник
G₁₇ ₅[6]₂	1200	60	5(1200)2	₅{6}₂	Шаблон:CDD	600	240	₅{}	то же, что и Шаблон:CDD $ℝ^{4}$ представление как {5,3,3}
		20		₅{5}₂	Шаблон:CDD				звёздчатый многоугольник
		20		₅{10/3}₂	Шаблон:CDD				звёздчатый многоугольник
		60		₅{3}₂	Шаблон:CDD				звёздчатый многоугольник
		60	2(1200)5	₂{6}₅	Шаблон:CDD	240	600	{}
		20		₂{5}₅	Шаблон:CDD				звёздчатый многоугольник
		20		₂{10/3}₅	Шаблон:CDD				звёздчатый многоугольник
		60		₂{3}₅	Шаблон:CDD				звёздчатый многоугольник
G₁₈ ₅[4]₃	1800	60	5(1800)3	₅{4}₃	Шаблон:CDD	600	360	₅{}	$ℝ^{4}$ представление как {5,3,3}
		15		₅{10/3}₃	Шаблон:CDD				звёздчатый многоугольник
		30		₅{3}₃	Шаблон:CDD				звёздчатый многоугольник
		30		₅{5/2}₃	Шаблон:CDD				звёздчатый многоугольник
		60	3(1800)5	₃{4}₅	Шаблон:CDD	360	600	₃{}
		15		₃{10/3}₅	Шаблон:CDD				звёздчатый многоугольник
		30		₃{3}₅	Шаблон:CDD				звёздчатый многоугольник
		30		₃{5/2}₅	Шаблон:CDD				звёздчатый многоугольник

Визуализация правильных комплексных многоугольников

Многоугольники вида _p{2r}_q можно визуализировать q цветных множеств p-рёбер. Каждое p-ребро выглядит как правильный многоугольник, но нет никаких граней.

2D-ортогональные проекции комплексных многоугольников $_{2} {r}_{q}$

Многогранники вида $_{2} {4}_{q}$ называются обобщёнными ортоплексами. Они имеют те же вершины, что и 4D q-q Шаблон:Не переведено 5, в которых вершины соединены 2-рёбрами.

₂{4}₂, Шаблон:CDD,
с 4 вершинами
и 4 рёбрами
₂{4}₃, Шаблон:CDD,
с 6 вершинами и
9 рёбрами Шаблон:Sfn
₂{4}₄, Шаблон:CDD,
с 8 вершинами
и 16 рёбрами
₂{4}₅, Шаблон:CDD,
с 10 вершинами
и 25 рёбрами
₂{4}₆, Шаблон:CDD,
с 12 вершинами
и 36 рёбрами
₂{4}₇, Шаблон:CDD,
с 14 вершинами
и 49 рёбрами
₂{4}₈, Шаблон:CDD,
с 16 вершинами
и 64 рёбрами
₂{4}₉, Шаблон:CDD,
с 18 вершинами
и 81 ребром
₂{4}₁₀, Шаблон:CDD,
с 20 вершинами
и 100 рёбрами

Комплексные многоугольники $_{p} {4}_{2}$

Многоугольники вида $_{p} {4}_{2}$ называются обобщёнными гиперкубами (квадратами для многоугольников). Многоугольники имеют те же вершины, что и 4D p-p дуопризмы, вершины соединены p-рёбрами. Вершины нарисованы зелёными и p-рёбра нарисованы поочерёдно красными и синими. Проекция слегка искажена для нечётных размерностей, чтобы сдвинуть накладывающиеся вершины от центра.

₂{4}₂, Шаблон:CDD или Шаблон:CDD,
с 4 вершинами
и 4 2-ребрами
₃{4}₂, Шаблон:CDD или Шаблон:CDD,
с 9 вершинами
и 6 (треугольными) 3-рёбрамиШаблон:Sfn
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 16 вершинами
и 8 (квадратными) 4-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 25 вершинами
и 10 (пятиугольными) 5-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 36 вершинами
и 12 (шестиугольными) 6-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 49 вершинами
и 14 (семиугольными) 7-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 64 вершинами
и 16 (восьмиугольными) 8-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
с 81 вершиной
и 18 (девятиугольными) 9-рёбрами
₄{4}₂, Шаблон:CDD или Шаблон:CDD,
со 100 вершинами
и 20 (десятиугольными) 10-рёбрами

3D-перспективные проекции комплексных многоугольников _p{4}₂

₃{4}₂, Шаблон:CDD или Шаблон:CDD
с 9 вершинами, 6 3-рёбер с 2 множествами цветов
₄{4}₂, Шаблон:CDD или Шаблон:CDD
с 16 вершинами, 8 4-рёбрами в 2 множествах столбцов (закрашены квадратные 4-рёбра)
₅{4}₂, Шаблон:CDD или Шаблон:CDD с 25 вершинами, 10 5-рёбрами в 2 множествах цветов

Другие комплексные многоугольники _p{r}₂

₃{6}₂, Шаблон:CDD или Шаблон:CDD, 24 вершины (чёрные) и 16 3-ребра, выкрашены в 2 цвета (красные и синие)Шаблон:Sfn
₃{8}₂, Шаблон:CDD или Шаблон:CDD, 72 вершины (чёрные) и 48 3-рёбер, выкрашенных в 2 цвета (красные и синие)Шаблон:Sfn

2D-ортогональные проекции комплексных многоугольников, _p{r}_p

Многоугольники вида $_{p} {r}_{p}$ имеют равное число вершин и рёбер. Они также самодвойственны.

Шаблон:Не переведено 5, Шаблон:CDD или Шаблон:CDD,
с 8 вершинами (чёрные) и 8 3-рёбер, выкрашенных в 2 цвета (красные и синие)Шаблон:Sfn
₃{4}₃, Шаблон:CDD или Шаблон:CDD,
с 24 вершинами и 24 3-ребра, показанных в 3 цвета Шаблон:Sfn
₄{3}₄, Шаблон:CDD или Шаблон:CDD,
с 24 вершинами и 24 4-рёбрами, показанных в 4 цвета Шаблон:Sfn
₃{5}₃, Шаблон:CDD или Шаблон:CDD,
со 120 вершинами и 120 3-рёберШаблон:Sfn
₅{3}₅, Шаблон:CDD или Шаблон:CDD,
со 120 вершинами и 120 5-рёберШаблон:Sfn

Правильные комплексные многогранники

В общем случае, правильный комплексный многогранник представляется символом Коксетера $_{p} {z_{1}}_{q} {z_{2}}_{r} {z_{3}}_{s} \dots$ или диаграммой Коксетера Шаблон:CDD…, имеющей симметрию $_{p} [z_{1}]_{q} [z_{2}]_{r} [z_{3}]_{s}$ … или Шаблон:CDD….Шаблон:Sfn

Существуют бесконечные семейства правильных комплексных многогранников, которые появляются во всех размерностях. Эти семейства обобщают гиперкубы и ортаэдры в вещественном пространстве. «Обобщённый гиперпрямоугольник» Шепарда обобщает гиперкуб. Он имеет символ $γ_{n}^{p} =_{p} {4}_{2} {3}_{2} \dots_{2} {3}_{2}$ и диаграмму Шаблон:CDD…Шаблон:CDD. Его группа симметрии имеет диаграмму $_{p} [4]_{2} [3]_{2} \dots_{2} [3]_{2}$ . В классификации Шепарда—Тодда это группа G(p, 1, n), обобщающая знаковые матрицы перестановок. Его двойственный правильный многогранник, «обобщённый кросс-многогранник», представляется символом $β_{n}^{p} =_{2} {3}_{2} {3}_{2} \dots_{2} {4}_{p}$ и диаграммой Шаблон:CDD…Шаблон:CDD Шаблон:Sfn.

1-мерный правильный комплексный многогранник в $ℂ^{1}$ представляется как Шаблон:CDD, имеет p вершин и имеет вещественное представление в виде правильного многоугольника {p}. Коксетер также даёт ему символ $γ_{1}^{p}$ или $β_{1}^{p}$ как 1-мерный обобщённый гиперкуб или кросс-многогранник. Его симметрия — $_{p} []$ или Шаблон:CDD, циклическая группа порядка p. В многогранниках более высокого порядка, $_{p} {}$ или Шаблон:CDD представляет элемент p-ребра. Так, 2-ребро, {} или Шаблон:CDD представляет обычное ребро между двумя вершинамиШаблон:Sfn.

Двойственный комплексный многогранник строится путём обмена k-го и (n-1-k)-го элементов n-многогранника. Например, двойственный комплексный многоугольник имеет вершины в середине каждого ребра, а новые рёбра имеют центры в старых вершинах. v-валентная вершина создаёт новое v-ребро, а e-ребро становится e-валентной вершинойШаблон:Sfn. Двойственный многогранник правильного комплексного многогранника имеет обратный символ (то есть записанный в обратном порядке). Правильные комплексные многогранники, имеющие симметричные символы, то есть $_{p} {q}_{p}$ , $_{p} {q}_{r} {q}_{p}$ , $_{p} {q}_{r} {s}_{r} {q}_{p}$ и т. д., являются самодвойственными.

Перечисление правильных комплексных многогранников

Коксетер перечислил незвёздчатые правильные комплексные многогранники в пространстве $ℂ^{3}$ , включая 5 правильных многогранников в $ℝ^{3}$ Шаблон:Sfn.

Правильный комплексный многогранник $_{p} {n_{1}}_{q} {n_{2}}_{r}$ или Шаблон:CDD, имеет Шаблон:CDD грани, Шаблон:CDD рёбра и Шаблон:CDD вершинные фигуры.

Комплексный правильный многогранник $_{p} {n_{1}}_{q} {n_{2}}_{r}$ требует, чтобы как g₁ = порядок( $_{p} [n_{1}]_{q}$ ), так и g₂ = порядок( $_{q} [n_{2}]_{r}$ ) были конечными.

Если g = порядок( $_{p} [n_{1}]_{q} [n_{2}]_{r}$ ), число вершин равно g/g₂ и число граней равно $g / g_{1}$ . Число рёбер равно g/pr.

Простран ство	Группа	Порядок	Число Коксетера	Многоугольник		Вершин	Рёбер		Граней		Вершинная фигура	Многоугольник ванн Осса	Примечания
$ℝ^{3}$	G(1,1,3) $_{2} [3]_{2} [3]_{2}$ = [3,3]	24	4	$α_{3} =_{2} {3}_{2} {3}_{2}$ = {3,3}	Шаблон:CDD	4	6	{}	4	{3}	{3}	—	Вещественный тетраэдр То же, что и Шаблон:CDD
$ℝ^{3}$	G₂₃ $_{2} [3]_{2} [5]_{2}$ = [3,5]	120	10	$_{2} {3}_{2} {5}_{2} = {3, 5}$	Шаблон:CDD	12	30	{}	20	{3}	{5}	—	Вещественный икосаэдр
$ℝ^{3}$	G₂₃ $_{2} [3]_{2} [5]_{2}$ = [3,5]	120	10	$_{2} {5}_{2} {3}_{2} = {5, 3}$	Шаблон:CDD	20	30	{}	12	{5}	{3}	—	Вещественный додекаэдр
$ℝ^{3}$	G(2,1,3) $_{2} [3]_{2} [4]_{2}$ = [3,4]	48	6	$β_{3}^{2} = β_{3} = {3, 4}$	Шаблон:CDD	6	12	{}	8	{3}	{4}	{4}	Вещественный октаэдр То же, что и {}+{}+{}, порядок 8 То же, что и Шаблон:CDD, порядок 24
$ℝ^{3}$	G(2,1,3) $_{2} [3]_{2} [4]_{2}$ = [3,4]	48	6	$γ_{3}^{2} = γ_{3} = {4, 3}$	Шаблон:CDD	8	12	{}	6	{4}	{3}	—	Вещественный куб То же, что и {}×{}×{} или Шаблон:CDD
$ℂ^{3}$	G(p,1,3) ₂[3]₂[4]_p p=2,3,4,…	6p³	3p	$β_{3}^{p} =_{2} {3}_{2} {4}_{p}$	Шаблон:CDD	3p	$3 p^{2}$	{}	p³	{3}	$_{2} {4}_{p}$	$_{2} {4}_{p}$	Обобщённый октаэдр То же, что и $_{p} {} +_{p} {} +_{p} {}$ , порядок p³ То же, что и Шаблон:CDD, порядок 6p²
$ℂ^{3}$	G(p,1,3) ₂[3]₂[4]_p p=2,3,4,…	6p³	3p	$γ_{3}^{p} =_{p} {4}_{2} {3}_{2}$	Шаблон:CDD	p³	3p²	_p{}	3p	$_{p} {4}_{2}$	{3}	—	Обобщённый куб То же, что и $_{p} {} \times_{p} {} \times_{p} {}$ или Шаблон:CDD
$ℂ^{3}$	G(3,1,3) ₂[3]₂[4]₃	162	9	$β_{3}^{3} =_{2} {3}_{2} {4}_{3}$	Шаблон:CDD	9	27	{}	27	{3}	$_{2} {4}_{3}$	$_{2} {4}_{3}$	То же, что и $_{3} {} +_{3} {} +_{3} {}$ , порядок 27 То же, что и Шаблон:CDD, порядок 54
$ℂ^{3}$	G(3,1,3) ₂[3]₂[4]₃	162	9	$γ_{3}^{3} =_{3} {4}_{2} {3}_{2}$	Шаблон:CDD	27	27	₃{}	9	₃{4}₂	{3}	—	То же, что и $_{3} {} \times_{3} {} \times_{3} {}$ или Шаблон:CDD
$ℂ^{3}$	G(4,1,3) $_{2} [3]_{2} [4]_{4}$	384	12	$β_{3}^{4} =_{2} {3}_{2} {4}_{4}$	Шаблон:CDD	12	48	{}	64	{3}	$_{2} {4}_{4}$	$_{2} {4}_{4}$	То же, что и $_{4} {} +_{4} {} +_{4} {}$ , порядок 64 То же, что и Шаблон:CDD, порядок 96
$ℂ^{3}$	G(4,1,3) $_{2} [3]_{2} [4]_{4}$	384	12	$γ_{3}^{4} =_{4} {4}_{2} {3}_{2}$	Шаблон:CDD	64	48	₄{}	12	$_{4} {4}_{2}$	{3}	—	То же, что и $_{4} {} \times_{4} {} \times_{4} {}$ или Шаблон:CDD
$ℂ^{3}$	G(5,1,3) ₂[3]₂[4]₅	750	15	$β_{3}^{5} =_{2} {3}_{2} {4}_{5}$	Шаблон:CDD	15	75	{}	125	{3}	$_{2} {4}_{5}$	$_{2} {4}_{5}$	То же, что и $_{5} {} +_{5} {} +_{5} {}$ , порядок 125 То же, что и Шаблон:CDD, порядок 150
$ℂ^{3}$	G(5,1,3) ₂[3]₂[4]₅	750	15	$γ_{3}^{5} =_{5} {4}_{2} {3}_{2}$	Шаблон:CDD	125	75	₅{}	15	$_{5} {4}_{2}$	{3}	—	То же, что и $_{5} {} \times_{5} {} \times_{5} {}$ или Шаблон:CDD
$ℂ^{3}$	G(6,1,3) ₂[3]₂[4]₆	1296	18	$β_{3}^{6} =_{2} {3}_{2} {4}_{6}$	Шаблон:CDD	36	108	{}	216	{3}	₂{4}₆	₂{4}₆	То же, что и ₆{}+₆{}+₆{}, порядок 216 То же, что и Шаблон:CDD, порядок 216
$ℂ^{3}$	G(6,1,3) ₂[3]₂[4]₆	1296	18	$γ_{3}^{6} =_{6} {4}_{2} {3}_{2}$	Шаблон:CDD	216	108	₆{}	18	₆{4}₂	{3}	—	То же, что и $_{6} {} \times_{6} {} \times_{6} {}$ или Шаблон:CDD
$ℂ^{3}$	G₂₅ ₃[3]₃[3]₃	648	9	₃{3}₃{3}₃	Шаблон:CDD	27	72	₃{}	27	₃{3}₃	₃{3}₃	₃{4}₂	То же, что и Шаблон:CDD. $ℝ^{6}$ представление как Шаблон:Не переведено 5 Шаблон:Не переведено 5
	G₂₆ ₂[4]₃[3]₃	1296	18	₂{4}₃{3}₃	Шаблон:CDD	54	216	{}	72	₂{4}₃	₃{3}₃	{6}
	G₂₆ ₂[4]₃[3]₃	1296	18	₃{3}₃{4}₂	Шаблон:CDD	72	216	₃{}	54	₃{3}₃	₃{4}₂	₃{4}₃	То же, что и Шаблон:CDD $ℝ^{6}$ представление как Шаблон:Не переведено 5

Визуализация правильных комплексных многогранников

2D-ортогональные проекции комплексных многогранников, _p{s}_t{r}_r

Вещественный {3,3}, Шаблон:CDD или Шаблон:CDD,
имеет 4 вершины, 6 рёбер и 4 грани
Шаблон:Не переведено 5, Шаблон:CDD или Шаблон:CDD,
имеет 27 вершин, 72 3-ребра и 27 граней, одна грань выделена синим цветомШаблон:Sfn.
₂{4}₃{3}₃, Шаблон:CDD,
имеет 54 вершины, 216 простых рёбер и 72 грани, одна грань выделена синим цветомШаблон:Sfn/
Шаблон:Не переведено 5, Шаблон:CDD или Шаблон:CDD,
имеет 72 вершины, 216 3-рёбер и 54 вершины, одна грань выделена синим цветомШаблон:Sfn.

Обобщённые октаэдры

Обобщённые октаэдры имеют построение как правильные формы Шаблон:CDD и как квазиправильные виды Шаблон:CDD. Все элементы являются симплексами.

Вещественный {3,4}, Шаблон:CDD или Шаблон:CDD, 6 вершин, 12 рёбер и 8 граней
₂{3}₂{4}₃, Шаблон:CDD или Шаблон:CDD, 9 вершин, 27 рёбер и 27 граней
₂{3}₂{4}₄, Шаблон:CDD или Шаблон:CDD, 12 вершин, 48 рёбер и 64 граней
₂{3}₂{4}₅, Шаблон:CDD или Шаблон:CDD, 15 вершин, 75 рёбер и 125 граней
₂{3}₂{4}₆, Шаблон:CDD или Шаблон:CDD, 18 вершин, 108 рёбер и 216 граней
₂{3}₂{4}₇, Шаблон:CDD или Шаблон:CDD, 21 вершина, 147 рёбер и 343 грани
₂{3}₂{4}₈, Шаблон:CDD или Шаблон:CDD, 24 вершины, 192 ребра и 512 граней
₂{3}₂{4}₉, Шаблон:CDD или Шаблон:CDD, 27 вершин, 243 ребра и 729 граней
₂{3}₂{4}₁₀, Шаблон:CDD или Шаблон:CDD, 30 вершин, 300 рёбер и 1000 граней

Обобщённые кубы

Обобщённые кубы имеют построение как правильные формы Шаблон:CDD и как призматические Шаблон:CDD, произведение трёх p-угольных 1-многогранников. Элементами являются обобщённые кубы меньшей размерности.

Вещественный {4,3}, Шаблон:CDD или Шаблон:CDD,
имеет 8 вершин, 12 рёбер и 6 граней
₃{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD,
имеет 27 вершин, 27 3-рёбер и 9 граней Шаблон:Sfn
₄{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 64 вершины, 48 рёбер и 12 граней
₅{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 125 вершин, 75 рёбер и 15 граней
₆{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, иммет 216 вершин, 108 рёбер и 18 граней
₇{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 343 вершины, 147 рёбер и 21 грань
₈{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 512 вершин, 192 ребра и 24 грани
₉{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 729 вершин, 243 ребра и 27 граней
₁₀{4}₂{3}₂, Шаблон:CDD или Шаблон:CDD, имеет 1000 вершин, 300 рёбер и 30 граней

Перечисление правильных комплексных 4-многогранников

Коксетер перечислил незвёздчатые правильные комплексные 4-многогранники в $ℂ^{4}$ , включая 6 выпуклых правильных 4-многогранников в $ℝ^{4}$ Шаблон:Sfn.

Простран- ство	Группа	Порядок	Число Коксетера	Многогранник	Вершины	Рёбра	Грани	Ячейки	Многоугольник ван Осса	Примечания
$ℝ^{4}$	G(1,1,4) $_{2} [3]_{2} [3]_{2} [3]_{2}$ = [3,3,3]	120	5	$α_{4} =_{2} {3}_{2} {3}_{2} {3}_{2}$ = {3,3,3} Шаблон:CDD	5	10 {}	10 {3}	5 {3,3}	—	Вещественный Пятиячейник (симплекс)
$ℝ^{4}$	G₂₈ $_{2} [3]_{2} [4]_{2} [3]_{2}$ = [3,4,3]	1152	12	$_{2} {3}_{2} {4}_{2} {3}_{2} = {3, 4, 3}$ Шаблон:CDD	24	96 {}	96 {3}	24 {3,4}	{6}	Вещественный двадцатичетырёхъячейник
	G₃₀ $_{2} [3]_{2} [3]_{2} [5]_{2}$ = [3,3,5]	14400	30	$_{2} {3}_{2} {3}_{2} {5}_{2} = {3, 3, 5}$ Шаблон:CDD	120	720 {}	1200 {3}	600 {3,3}	{10}	Вещественный шестисотячейник
	G₃₀ $_{2} [3]_{2} [3]_{2} [5]_{2}$ = [3,3,5]	14400	30	$_{2} {5}_{2} {3}_{2} {3}_{2} = {5, 3, 3}$ Шаблон:CDD	600	1200 {}	720 {5}	120 {5,3}	{10}	Вещественный стодвадцатиячейник
$ℝ^{4}$	G(2,1,4) $_{2} [3]_{2} [3]_{2} [4]_{p}$ =[3,3,4]	384	8	$β_{4}^{2} = β_{4} = {3, 3, 4}$ Шаблон:CDD	8	24 {}	32 {3}	16 {3,3}	{4}	Вещественный шестнадцатиячейник То же, что и Шаблон:CDD, порядок 192
$ℝ^{4}$	G(2,1,4) $_{2} [3]_{2} [3]_{2} [4]_{p}$ =[3,3,4]	384	8	$γ_{4}^{2} = γ_{4} = {4, 3, 3}$ Шаблон:CDD	16	32 {}	24 {4}	8 {4,3}	—	Вещественный тессеракт То же, что и {}⁴ или Шаблон:CDD, порядок 16
$ℂ^{4}$	G(p,1,4) ₂[3]₂[3]₂[4]_p p=2,3,4,…	24p⁴	4p	$β_{4}^{p} =_{2} {3}_{2} {3}_{2} {4}_{p}$ Шаблон:CDD	4p	6p² {}	4p³ {3}	p⁴ {3,3}	₂{4}_p	Обобщённый 4-ортоплекс То же, что и Шаблон:CDD, порядок 24p³
$ℂ^{4}$	G(p,1,4) ₂[3]₂[3]₂[4]_p p=2,3,4,…	24p⁴	4p	$γ_{4}^{p} =_{p} {4}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	p⁴	4p³ _p{}	6p² _p{4}₂	4p $_{p} {4}_{2} {3}_{2}$	—	Обобщённый тессеракт То же, что и _p{}⁴ или Шаблон:CDD, порядок p⁴
$ℂ^{4}$	G(3,1,4) ₂[3]₂[3]₂[4]₃	1944	12	$β_{4}^{3} =_{2} {3}_{2} {3}_{2} {4}_{3}$ Шаблон:CDD	12	54 {}	108 {3}	81 {3,3}	₂{4}₃	Обобщённый 4-ортоплекс То же, что и Шаблон:CDD, порядок 648
$ℂ^{4}$	G(3,1,4) ₂[3]₂[3]₂[4]₃	1944	12	$γ_{4}^{3} =_{3} {4}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	81	108 ₃{}	54 ₃{4}₂	12 ₃{4}₂{3}₂	—	То же, что и ₃{}⁴ или Шаблон:CDD, порядок 81
$ℂ^{4}$	G(4,1,4) ₂[3]₂[3]₂[4]₄	6144	16	$β_{4}^{4} =_{2} {3}_{2} {3}_{2} {4}_{4}$ Шаблон:CDD	16	96 {}	256 {3}	64 {3,3}	$_{2} {4}_{4}$	То же, что и Шаблон:CDD, порядок 1536
$ℂ^{4}$	G(4,1,4) ₂[3]₂[3]₂[4]₄	6144	16	$γ_{4}^{4} =_{4} {4}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	256	256 ₄{}	96 ₄{4}₂	16 ₄{4}₂{3}₂	—	То же, что и ₄{}⁴ или Шаблон:CDD, порядок 256
$ℂ^{4}$	G(5,1,4) ₂[3]₂[3]₂[4]₅	15000	20	$β_{4}^{5} =_{2} {3}_{2} {3}_{2} {4}_{5}$ Шаблон:CDD	20	150 {}	500 {3}	625 {3,3}	₂{4}₅	То же, что и Шаблон:CDD, порядок 3000
$ℂ^{4}$	G(5,1,4) ₂[3]₂[3]₂[4]₅	15000	20	$γ_{4}^{5} =_{5} {4}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	625	500 ₅{}	150 ₅{4}₂	20 $_{5} {4}_{2} {3}_{2}$	—	То же, что и ₅{}⁴ или Шаблон:CDD, порядок 625
$ℂ^{4}$	G(6,1,4) ₂[3]₂[3]₂[4]₆	31104	24	$β_{4}^{6} =_{2} {3}_{2} {3}_{2} {4}_{6}$ Шаблон:CDD	24	216 {}	864 {3}	1296 {3,3}	$_{2} {4}_{6}$	То же, что и Шаблон:CDD, порядок 5184
$ℂ^{4}$	G(6,1,4) ₂[3]₂[3]₂[4]₆	31104	24	$γ_{4}^{6} =_{6} {4}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	1296	864 ₆{}	216 ₆{4}₂	24 $_{6} {4}_{2} {3}_{2}$	—	То же, что и ₆{}⁴ или Шаблон:CDD, порядок 1296
$ℂ^{4}$	G₃₂ ₃[3]₃[3]₃[3]₃	155520	30	₃{3}₃{3}₃{3}₃ Шаблон:CDD	240	2160 ₃{}	2160 ₃{3}₃	240 ₃{3}₃{3}₃	₃{4}₃	Шаблон:Не переведено 5 $ℝ^{8}$ представление как Шаблон:Не переведено 5

Визуализация правильных комплексных 4-многогранников

Вещественный {3,3,3}, Шаблон:CDD, имеет 5 вершин, 10 рёбер, 10 {3} граней и 5 {3,3} ячеек
Вещественный {3,4,3}, Шаблон:CDD, имеет 24 вершины, 96 рёбер, 96 {3} граней и 24 {3,4} ячейки
Вещественный {5,3,3}, Шаблон:CDD, имеет 600 вершин, 1200 рёбер, 720 {5} граней и 120 {5,3} ячеек
Вещественный {3,3,5}, Шаблон:CDD, имеет 120 вершин, 720 рёбер, 1200 {3} граней и 600 {3,3} ячеек
Шаблон:Не переведено 5, Шаблон:CDD,
имеет 240 вершин, 2160 3-рёбер, 2160 3{3}3 граней и 240 3{3}3{3}3 ячеек

Обобщённые 4-ортоплексы

Обобщённые 4-ортоплексы имеют построение как правильные види Шаблон:CDD и квазиправильные виды какШаблон:CDD. Все элементы являются симплексами.

Вещественный {3,3,4}, Шаблон:CDD или Шаблон:CDD,
с 8 вершинами, 24 ребра, 32 грани и 16 ячеек
₂{3}₂{3}₂{4}₃, Шаблон:CDD или Шаблон:CDD,
с 12 вершинами, 54 ребра, 108 граней и 81 ячейка
₂{3}₂{3}₂{4}₄, Шаблон:CDD или Шаблон:CDD,
с 16 вершинами, 96 рёбрами, 256 рёбрами и 256 ячеек
₂{3}₂{3}₂{4}₅, Шаблон:CDD или Шаблон:CDD,
с 20 вершинами, 150 рёбрами, 500 граней и 625 ячеек
₂{3}₂{3}₂{4}₆, Шаблон:CDD или Шаблон:CDD,
с 24 вершинами, 216 рёбрами, 864 грани и 1296 ячеек
₂{3}₂{3}₂{4}₇, Шаблон:CDD или Шаблон:CDD,
с 28 вершинами, 294 рёбрами, 1372 грани и 2401 ячейка
₂{3}₂{3}₂{4}₈, Шаблон:CDD или Шаблон:CDD,
с 32 вершинами, 384 рёбрами, 2048 граней и 4096 ячеек
₂{3}₂{3}₂{4}₉, Шаблон:CDD или Шаблон:CDD,
с 36 вершинами, 486 рёбрами, 2916 граней и 6561 ячейка
₂{3}₂{3}₂{4}₁₀, Шаблон:CDD или Шаблон:CDD,
с 40 вершинами, 600 рёбрами, 4000 граней и 10000 ячеек

Обобщённые 4-кубы

Обобщённые тессеракты имеют построение как правильные формы Шаблон:CDD и как призматические виды Шаблон:CDD, произведение четырёх p-угольных 1-многогранников. Элементами являются обобщённые кубы меньшей размерности.

Вещественный {4,3,3}, Шаблон:CDD или Шаблон:CDD, 16 вершин, 32 ребра, 24 грани и 8 ячеек
$_{3} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
81 вершина, 108 рёбер, 54 грани и 12 ячеек
$_{4} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
256 вершин, 96 рёбер, 96 граней и 16 ячеек
$_{5} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
625 вершин, 500 рёбер, 150 граней и 20 ячеек
$_{6} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
1296 вершин, 864 ребра, 216 граней и 24 ячейки
$_{7} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
2401 вершина, 1372 ребра, 294 грани и 28 ячеек
$_{8} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
4096 вершин, 2048 рёбер, 384 грани и 32 ячейки
$_{9} {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
6561 вершина, 2916 рёбер, 486 граней и 36 ячеек
$_{1} 0 {4}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD или Шаблон:CDD,
10000 вершин, 4000 рёбер, 600 граней и 40 ячеек

Перечисление правильных комплексных 5-многогранников

Правильные комплексные 5-многогранники в $ℂ^{5}$ и более высоких размерностях существуют в виде трёх семейств, вещественные симплексы, обобщённые гиперкубы и ортоплексы.

Простран- ство	Группа	Порядок	Многогранник	Вершины	Рёбра	Грани	Ячейки	4-грани	Много- угольник ван Осса	Примечания
$ℝ^{5}$	G(1,1,5) = [3,3,3,3]	720	α₅ = {3,3,3,3} Шаблон:CDD	6	15 {}	20 {3}	15 {3,3}	6 {3,3,3}	—	Вещественный правильный 5-симплекс
$ℝ^{5}$	G(2,1,5) =[3,3,3,4]	3840	$β_{5}^{2} = β_{5} = {3, 3, 3, 4}$ Шаблон:CDD	10	40 {}	80 {3}	80 {3,3}	32 {3,3,3}	{4}	Вещественный 5-ортоплекс То же, что и Шаблон:CDD, порядок 1920
$ℝ^{5}$	G(2,1,5) =[3,3,3,4]	3840	$γ_{5}^{2} = γ_{5} = {4, 3, 3, 3}$ Шаблон:CDD	32	80 {}	80 {4}	40 {4,3}	10 {4,3,3}	—	Вещественный пентеракт То же, что и {}⁵ или Шаблон:CDD, порядок 32
$ℂ^{5}$	G(p,1,5) ₂[3]₂[3]₂[3]₂[4]_p	120p⁵	$β_{5}^{p} =_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{p}$ Шаблон:CDD	5p	10p² {}	10p³ {3}	5p⁴ {3,3}	p⁵ {3,3,3}	$_{2} {4}_{p}$	Обобщённый 5-ортоплекс То же, что и Шаблон:CDD, порядок 120p⁴
$ℂ^{5}$	G(p,1,5) ₂[3]₂[3]₂[3]₂[4]_p	120p⁵	$γ_{5}^{p} =_{p} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	p⁵	5p⁴ _p{}	10p³ $_{p} {4}_{2}$	10p² $_{p} {4}_{2} {3}_{2}$	5p $_{p} {4}_{2} {3}_{2} {3}_{2}$	—	Обобщённый пентеракт То же, что и _p{}⁵ или Шаблон:CDD, порядок p⁵
$ℂ^{5}$	G(3,1,5) $_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{3}$	29160	$β_{5}^{3} =_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{3}$ Шаблон:CDD	15	90 {}	270 {3}	405 {3,3}	243 {3,3,3}	₂{4}₃	То же, что и Шаблон:CDD, порядок 9720
$ℂ^{5}$	G(3,1,5) $_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{3}$	29160	$γ_{5}^{3} =_{3} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	243	405 ₃{}	270 $_{3} {4}_{2}$	90 $_{3} {4}_{2} {3}_{2}$	15 $_{3} {4}_{2} {3}_{2} {3}_{2}$	—	То же, что и ₃{}⁵ или Шаблон:CDD, порядок 243
$ℂ^{5}$	G(4,1,5) ₂[3]₂[3]₂[3]₂[4]₄	122880	$β_{5}^{4} =_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{4}$ Шаблон:CDD	20	160 {}	640 {3}	1280 {3,3}	1024 {3,3,3}	₂{4}₄	То же, что и Шаблон:CDD, порядок 30720
$ℂ^{5}$	G(4,1,5) ₂[3]₂[3]₂[3]₂[4]₄	122880	$γ_{5}^{4} =_{4} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	1024	1280 ₄{}	640 ₄{4}₂	160 $_{4} {4}_{2} {3}_{2}$	20 $_{4} {4}_{2} {3}_{2} {3}_{2}$	—	То же, что и ₄{}⁵ или Шаблон:CDD, порядок 1024
$ℂ^{5}$	G(5,1,5) ₂[3]₂[3]₂[3]₂[4]₅	375000	$β_{5}^{5} =_{2} {3}_{2} {3}_{2} {3}_{2} {5}_{5}$ Шаблон:CDD	25	250 {}	1250 {3}	3125 {3,3}	3125 {3,3,3}	₂{5}₅	То же, что и Шаблон:CDD, порядок 75000
$ℂ^{5}$	G(5,1,5) ₂[3]₂[3]₂[3]₂[4]₅	375000	$γ_{5}^{5} =_{5} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	3125	3125 ₅{}	1250 $_{5} {5}_{2}$	250 $_{5} {5}_{2} {3}_{2}$	25 $_{5} {4}_{2} {3}_{2} {3}_{2}$	—	То же, что и ₅{}⁵ или Шаблон:CDD, порядок 3125
$ℂ^{5}$	G(6,1,5) ₂[3]₂[3]₂[3]₂[4]₆	933210	$β_{5}^{6} =_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{6}$ Шаблон:CDD	30	360 {}	2160 {3}	6480 {3,3}	7776 {3,3,3}	$_{2} {4}_{6}$	То же, что и Шаблон:CDD, порядок 155520
$ℂ^{5}$	G(6,1,5) ₂[3]₂[3]₂[3]₂[4]₆	933210	$γ_{5}^{6} =_{6} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	7776	6480 ₆{}	2160 $_{6} {4}_{2}$	360 $_{6} {4}_{2} {3}_{2}$	30 $_{6} {4}_{2} {3}_{2} {3}_{2}$	—	То же, что и ₆{}⁵ или Шаблон:CDD, порядок 7776

Визуализация правильных комплексных 5-многогранников

Обобщёные 5-ортоплексы

Обобщённые 5-ортоплексы имеют построение как правильные формы Шаблон:CDD и как квазиправильные Шаблон:CDD. Все элементы являются симплексами.

Вещественный {3,3,3,4}, Шаблон:CDD,
10 вершин, 40 рёбер,
80 граней, 80 ячеек и 32 4-грани
₂{3}₂{3}₂{3}₂{4}₃, Шаблон:CDD,
15 вершин, 90 рёбер,
270 граней, 405 ячеек и 243 4-грани
₂{3}₂{3}₂{3}₂{4}₄, Шаблон:CDD,
20 вершин, 160 рёбер,
640 граней, 1280 ячеек и 1024 4-грани
₂{3}₂{3}₂{3}₂{4}₅, Шаблон:CDD,
25 вершин, 250 рёбер,
1250 граней, 3125 ячеек и 3125 4 граней
₂{3}₂{3}₂{3}₂{4}₆, Шаблон:CDD,
30 вершин, 360 рёбер,
2160 граней, 6480 ячеек, 7776 4-граней
₂{3}₂{3}₂{3}₂{4}₇, Шаблон:CDD,
35 вершин, 490 рёбер,
3430 граней, 12005 ячеек, 16807 4-граней
₂{3}₂{3}₂{3}₂{4}₈, Шаблон:CDD,
40 вершин, 640 рёбер,
5120 граней, 20480 ячеек, 32768 4-граней
₂{3}₂{3}₂{3}₂{4}₉, Шаблон:CDD,
45 вершин, 810 рёбер, 7290 граней, 32805 ячеек, 59049 4-граней
₂{3}₂{3}₂{3}₂{4}₁₀, Шаблон:CDD,
50 вершин, 1000 рёбер,
10000 граней, 50000 ячеек, 100000 4-граней

Обобщённые пентеракты

Обобщённые пентеракты имеют построение как правильные формы Шаблон:CDD и как призматические Шаблон:CDD, произведение пяти p-угольных 1-многогранников. Элементами являются обобщённые кубы меньшей размерности.

Вещественный {4,3,3,3}, Шаблон:CDD,
32 вершины, 80 рёбер,
80 граней, 40 ячеек и 10 4-граней
₃{4}₂{3}₂{3}₂{3}₂, Шаблон:CDD,
243 вершины, 405 рёбер, 270 граней, 90 ячеек и 15 4-граней
₄{4}₂{3}₂{3}₂{3}₂, Шаблон:CDD,
1024 вершины, 1280 рёбер,
640 граней, 160 ячеек и 20 4-граней
₅{4}₂{3}₂{3}₂{3}₂, Шаблон:CDD,
3125 вершин, 3125 рёбер,
1250 граней, 250 ячеек и 25 4-граней
₆{4}₂{3}₂{3}₂{3}₂, Шаблон:CDD,
7776 вершин, 6480 рёбер,
2160 граней, 360 ячеек и 30 4-граней

Перечисление правильных комплексных 6-многогранников

Простран- ство	Группа	Порядок	Многогранник	Вершины	Рёбра	Грани	Ячейки	4-грани	5-грани	Много- угольник ван Осса	Примечания
$ℝ^{6}$	G(1,1,6) = [3,3,3,3,3]	720	α₆ = {3,3,3,3,3} Шаблон:CDD	7	21 {}	35 {3}	35 {3,3}	21 {3,3,3}	7 {3,3,3,3}	—	Вещественный 6-симплекс
$ℝ^{6}$	G(2,1,6) [3,3,3,4]	46080	$β_{6}^{2} = β_{6} = {3, 3, 3, 4}$ Шаблон:CDD	12	60 {}	160 {3}	240 {3,3}	192 {3,3,3}	64 {3,3,3,3}	{4}	Вещественный 6-ортоплекс То же, что и Шаблон:CDD, порядок 23040
$ℝ^{6}$	G(2,1,6) [3,3,3,4]	46080	$γ_{6}^{2} = γ_{6} = {4, 3, 3, 3}$ Шаблон:CDD	64	192 {}	240 {4}	160 {4,3}	60 {4,3,3}	12 {4,3,3,3}	—	Вещественный гексеракт То же, что и {}⁶ или Шаблон:CDD, порядок 64
$ℂ^{6}$	G(p,1,6) $_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{p}$	720p⁶	$β_{6}^{p} =_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{p}$ Шаблон:CDD	6p	15p² {}	20p³ {3}	15p⁴ {3,3}	6p⁵ {3,3,3}	p⁶ {3,3,3,3}	$_{2} {4}_{p}$	Обобщённый 6-ортоплекс То же, что и Шаблон:CDD, порядок 720p⁵
$ℂ^{6}$	G(p,1,6) $_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{p}$	720p⁶	$γ_{6}^{p} =_{p} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$ Шаблон:CDD	p⁶	6p⁵ _p{}	15p⁴ _p{4}₂	20p³ $_{p} {4}_{2} {3}_{2}$	15p² $_{p} {4}_{2} {3}_{2} {3}_{2}$	6p $_{p} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$	—	Обобщённый гексеракт То же, что и _p{}⁶ или Шаблон:CDD, порядок p⁶

Визуализация правильных комплексных 6-многогранников

Обобщённые 6-ортоплексы

Обобщённые 6-ортоплексы имеют построение как правильные формы Шаблон:CDD и как квазиправильные формы Шаблон:CDD. Все элемент являются симплексами.

Вещественный {3,3,3,3,4}, Шаблон:CDD,
12 вершин, 60 рёбер, 160 граней, 240 ячеек, 192 4-грани и 64 5-грани
$_{2} {3}_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{3}$ , Шаблон:CDD,
18 вершин, 135 рёбер, 540 граней, 1215 ячеек, 1458 4-граней и 729 5-граней
₂{3}₂{3}₂{3}₂{3}₂{4}₄, Шаблон:CDD,
24 вершины, 240 рёбер, 1280 граней, 3840 ячеек, 6144 4-грани и 4096 5-граней
₂{3}₂{3}₂{3}₂{3}₂{4}₅, Шаблон:CDD,
30 вершин, 375 рёбер, 2500 граней, 9375 ячеек, 18750 4-граней и 15625 5-граней
₂{3}₂{3}₂{3}₂{3}₂{4}₆, Шаблон:CDD,
36 вершин, 540 рёбер, 4320 граней, 19440 ячеек, 46656 4-граней и 46656 5-граней
₂{3}₂{3}₂{3}₂{3}₂{4}₇, Шаблон:CDD,
42 вершины, 735 рёбер, 6860 граней, 36015 ячеек, 100842 4-грани, 117649 5-граней
₂{3}₂{3}₂{3}₂{3}₂{4}₈, Шаблон:CDD,
48 вершин, 960 рёбер, 10240 граней, 61440 ячеек, 196608 4-граней, 262144 5-грани
₂{3}₂{3}₂{3}₂{3}₂{4}₉, Шаблон:CDD,
54 вершины, 1215 рёбер, 14580 граней, 98415 ячеек, 354294 4-грани, 531441 5-грань
₂{3}₂{3}₂{3}₂{3}₂{4}₁₀, Шаблон:CDD,
60 вершин, 1500 рёбер, 20000 граней, 150000 ячеек, 600000 4-граней, 1000000 5-граней

Обобщённые 6-кубы (гексеракты)

Обобщённые 6-кубы имеют построение как правильные формы Шаблон:CDD и призматические формы Шаблон:CDD, произведение шести p-угольных 1-угольников. Элементами являются обобщённые кубы меньших размерностей.

Вещественный {3,3,3,3,3,4}, Шаблон:CDD, 64 вершины, 192 ребра, 240 граней, 160 ячеек, 60 4-граней и 12 5-граней
$_{3} {4}_{2} {3}_{2} {3}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD, 729 вершин, 1458 рёбер, 1215 граней, 540 ячеек, 135 4-граней и 18 5-граней
$_{4} {4}_{2} {3}_{2} {3}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD, 4096 вершин, 6144 ребра, 3840 граней, 1280 ячеек, 240 4-граней и 24 5-грани
$_{5} {4}_{2} {3}_{2} {3}_{2} {3}_{2} {3}_{2}$ , Шаблон:CDD, 15625 вершин, 18750 рёбер, 9375 граней, 2500 ячеек, 375 4-граней и 30 5-граней

Перечисление правильных комплексных бесконечногранников

Некоторые подгруппы бесконечноугольных групп Шеперда

Коксетер перечислил незвёздные правильные комплексные бесконечногранники и сотыШаблон:Sfn.

Для каждой размерности существует 12 бесконечногранников с символами $δ_{n + 1}^{p, r}$ существуют в любых размерностях $ℂ^{n}$ , или $ℝ^{n}$ if p=q=2. Коксетер называл их обобщёнными кубическими сотами для n>Шаблон:Sfn.

Каждый имеет пропорциональное число элементов, задаваемое формулами:

k-граней =

(\binom{n}{k}) p^{n - k} r^{k}

, где

(\binom{n}{m}) = \frac{n!}{m! (n - m)!}

и n! означает факториал числа n.

Правильные комплексные 1-многогранники

Единственным правильным комплексным 1-многогранником является _∞{}, или Шаблон:CDD. Его вещественным представлением служит апейрогон {∞}, или Шаблон:CDD.

Правильные комплексные апейрогоны

Комплексные бесконечноугольники ранга 2 имеют симметрию _p[q]_r, где 1/p + 2/q + 1/r = 1. Коксетер выражает их как $δ_{2}^{p, r}$ , где q ограничено выражением $q = 2 / (1 - (p + r) / p r)$ Шаблон:Sfn.

Существует 8 решений:

$_{2} [\infty]_{2}$	$_{3} [12]_{2}$	$_{4} [8]_{2}$	$_{6} [6]_{2}$	$_{3} [6]_{3}$	$_{6} [4]_{3}$	$_{4} [4]_{4}$	$_{6} [3]_{6}$
Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD

Есть два исключённых решения с нечётным q и неравными p и r, это $_{1} 0 [5]_{2}$ и $_{1} 2 [3]_{4}$ , Шаблон:CDD или Шаблон:CDD.

Правильный комплексный бесконечноугольник $_{p} {q}_{r}$ имеет p-рёберные и q-гональные вершинные фигуры. Двойственный бесконечноугольник тела $_{p} {q}_{r}$ — это $_{r} {q}_{p}$ . Бесконечноугольник вида $_{p} {q}_{p}$ самодвойственен. Группы вида $_{p} [2 q]_{2}$ имеют половину симметрии $_{p} [q]_{p}$ , так что бесконечноугольник Шаблон:CDD — это то же, что и квазирегулярный многогранник Шаблон:CDD Шаблон:Sfn.

Апейрогоны можно представить на комплексной плоскости четырьмя различными расположениями вершин. Апейрогоны вида $_{2} {q}_{r}$ имеют расположение вершин {q/2,p}, апейрогоны вида $_{p} {q}_{2}$ имеют расположение вершин r{p,q/2}, а апейрогоны вида $_{p} {4}_{r}$ имеют расположение вершин {p,r}.

Если включить аффинные узлы $ℂ^{2}$ , добавляется ещё 3 бесконечных решения $_{\infty} [2]_{\infty},_{\infty} [4]_{2},_{\infty} [3]_{3}$ (Шаблон:CDD, Шаблон:CDD и Шаблон:CDD). Первое решение является подгруппой с индексом 2 второго. Вершины этих бесконечноугольников существует в $ℂ^{1}$ .

Ранг 2
Простран ство	Группа	Апейрогон		Ребро	$ℝ^{2}$ предст.Шаблон:Sfn	Примечания
$ℝ^{1}$	₂[∞]₂ = [∞]	$δ_{2}^{2, 2} = \infty$	Шаблон:CDD	{}		Вещественный бесконечноугольник То же, что и Шаблон:CDD
$ℂ^{2}$ / $ℂ^{1}$	_∞[4]₂	_∞{4}₂	Шаблон:CDD	_∞{}	{4,4}	То же, что и Шаблон:CDD
$ℂ^{1}$	_∞[3]₃	_∞{3}₃	Шаблон:CDD	_∞{}	{3,6}	То же, что и Шаблон:CDD
$ℂ^{1}$	_p[q]_r	$δ_{2}^{p, r} =_{p} {q}_{r}$	Шаблон:CDD	_p{}
$ℂ^{1}$	$_{3} [12]_{2}$	$δ_{2}^{3, 2} =_{3} {12}_{2}$	Шаблон:CDD	₃{}	r{3,6}	То же, что и Шаблон:CDD
$ℂ^{1}$	$_{3} [12]_{2}$	$δ_{2}^{2, 3} =_{2} {12}_{3}$	Шаблон:CDD	{}	{6,3}
$ℂ^{1}$	₃[6]₃	$δ_{2}^{3, 3} =_{3} {6}_{3}$	Шаблон:CDD	₃{}	{3,6}	То же, что и Шаблон:CDD
$ℂ^{1}$	₄[8]₂	$δ_{2}^{4, 2} =_{4} {8}_{2}$	Шаблон:CDD	₄{}	{4,4}	То же, что и Шаблон:CDD
$ℂ^{1}$	₄[8]₂	$δ_{2}^{2, 4} =_{2} {8}_{4}$	Шаблон:CDD	{}	{4,4}
$ℂ^{1}$	₄[4]₄	$δ_{2}^{4, 4} =_{4} {4}_{4}$	Шаблон:CDD	₄{}	{4,4}	То же, что и Шаблон:CDD
$ℂ^{1}$	₆[6]₂	$δ_{2}^{6, 2} =_{6} {6}_{2}$	Шаблон:CDD	₆{}	r{3,6}	То же, что и Шаблон:CDD
$ℂ^{1}$	₆[6]₂	$δ_{2}^{2, 6} =_{2} {6}_{6}$	Шаблон:CDD	{}	{3,6}
$ℂ^{1}$	₆[4]₃	$δ_{2}^{6, 3} =_{6} {4}_{3}$	Шаблон:CDD	₆{}	{6,3}
$ℂ^{1}$	₆[4]₃	$δ_{2}^{3, 6} =_{3} {4}_{6}$	Шаблон:CDD	₃{}	{3,6}
$ℂ^{1}$	₆[3]₆	$δ_{2}^{6, 6} =_{6} {3}_{6}$	Шаблон:CDD	₆{}	{3,6}	То же, что и Шаблон:CDD

Правильные комплексные бесконечногранники (трёхмерное пространство)

Существует 22 правильных комплексных бесконечногранника вида $_{p} {a}_{q} {b}_{r}$ . 8 тел самодвойственны (p=r и a=b), а 14 существуют как двойственные пары многогранников. Три из них полностью вещественны (p=q=r=2).

Коксетер дал двенадцати из них символы $δ_{3}^{p, r}$ (или $_{p} {4}_{2} {4}_{r}$ ) и они являются правильными видами произведения бесконечногранников $δ_{2}^{p, r} \times δ_{2}^{p, r}$ или $_{p} {q}_{r} \times_{p} {q}_{r}$ , где q вычисляется из p и r.

Многогранники Шаблон:CDD — это то же, что и Шаблон:CDD, так же, как и Шаблон:CDD для p,r=2,3,4,6. Также, Шаблон:CDD = Шаблон:CDD Шаблон:Sfn.

Ранг 3
Простран- ство	Группа	Бесконечно- гранник		Вершины	Рёбра		Грани		Бесконечно- гранник ван Осса	Примечания
$ℂ^{3}$	₂[3]₂[4]_∞	_∞{4}₂{3}₂	Шаблон:CDD			_∞{}		_∞{4}₂		То же, что и _∞{}×_∞{}×_∞{} или Шаблон:CDD Вещественное представление Шаблон:Не переведено 5
$ℂ^{2}$	_p[4]₂[4]_r	_p{4}₂{4}_r	Шаблон:CDD	p²	2pq	_p{}	r²	_p{4}₂	₂{q}_r	То же, что и Шаблон:CDD, p,r=2,3,4,6
$ℝ^{2}$	[4,4]	$δ_{3}^{2, 2} = {4, 4}$	Шаблон:CDD	4	8	{}	4	{4}	{∞}	Вещественная квадратная мозаика То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD
$ℂ^{2}$	₃[4]₂[4]₂ ₃[4]₂[4]₃ ₄[4]₂[4]₂ ₄[4]₂[4]₄ ₆[4]₂[4]₂ ₆[4]₂[4]₃ ₆[4]₂[4]₆	₃{4}₂{4}₂ ₂{4}₂{4}₃ ₃{4}₂{4}₃ ₄{4}₂{4}₂ ₂{4}₂{4}₄ ₄{4}₂{4}₄ ₆{4}₂{4}₂ ₂{4}₂{4}₆ ₆{4}₂{4}₃ ₃{4}₂{4}₆ ₆{4}₂{4}₆	Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD Шаблон:CDD	9 4 9 16 4 16 36 4 36 9 36	12 12 18 16 16 32 24 24 36 36 72	₃{} {} ₃{} ₄{} {} ₄{} ₆{} {} ₆{} ₃{} ₆{}	4 9 9 4 16 16 4 36 9 36 36	₃{4}₂ {4} ₃{4}₂ ₄{4}₂ {4} ₄{4}₂ ₆{4}₂ {4} ₆{4}₂ ₃{4}₂ ₆{4}₂	_p{q}_r	То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD То же, что и Шаблон:CDD

Простран- ство	Группа	Бесконечногранник		Вершины	Рёбра		Грани		много- угольник ван Осса	Примечания
$ℂ^{2}$	₂[4]_r[4]₂	₂{4}_r{4}₂	Шаблон:CDD	2		{}	2	_p{4}_2'	₂{4}_r	То же, что и Шаблон:CDD и Шаблон:CDD, r = 2,3,4,6
$ℝ^{2}$	[4,4]	{4,4}	Шаблон:CDD	2	4	{}	2	{4}	{∞}	То же, что и Шаблон:CDD и Шаблон:CDD
$ℂ^{2}$	$_{2} [4]_{3} [4]_{2}$ $_{2} [4]_{4} [4]_{2}$ $_{2} [4]_{6} [4]_{2}$	$_{2} {4}_{3} {4}_{2}$ $_{2} {4}_{4} {4}_{2}$ $_{2} {4}_{6} {4}_{2}$	Шаблон:CDD Шаблон:CDD Шаблон:CDD	2	9 16 36	{}	2	$_{2} {4}_{3}$ $_{2} {4}_{4}$ $_{2} {4}_{6}$	$_{2} {q}_{r}$	То же, что и Шаблон:CDD и Шаблон:CDD То же, что и Шаблон:CDD и Шаблон:CDD То же, что и Шаблон:CDD и Шаблон:CDD Шаблон:Sfn

Простран- ство	Группа	Многогранник		Вершины	Рёбра		Грани		бесконечно- угольник ван Осса	Примечания
$ℝ^{2}$	₂[6]₂[3]₂ = [6,3]	{3,6}	Шаблон:CDD	1	3	{}	2	{3}	{∞}	Вещественная треугольная мозаика
$ℝ^{2}$	₂[6]₂[3]₂ = [6,3]	{6,3}	Шаблон:CDD	2	3	{}	1	{6}	—	Вещественная шестиугольная мозаика
$ℂ^{2}$	₃[4]₃[3]₃	₃{3}₃{4}₃	Шаблон:CDD	1	8	₃{}	3	₃{3}₃	₃{4}₆	То же, что и Шаблон:CDD
$ℂ^{2}$	₃[4]₃[3]₃	₃{4}₃{3}₃	Шаблон:CDD	3	8	₃{}	2	₃{4}₃	₃{12}₂
$ℂ^{2}$	₄[3]₄[3]₄	₄{3}₄{3}₄	Шаблон:CDD	1	6	₄{}	1	₄{3}₄	₄{4}₄	Самодвойственный, то же, что и Шаблон:CDD
$ℂ^{2}$	₄[3]₄[4]₂	₄{3}₄{4}₂	Шаблон:CDD	1	12	₄{}	3	₄{3}₄	₂{8}₄	То же, что и Шаблон:CDD
$ℂ^{2}$	₄[3]₄[4]₂	₂{4}₄{3}₄	Шаблон:CDD	3	12	{}	1	₂{4}₄	₄{4}₄

Правильные комплексные 3-бесконечногранники

Существует 16 правильных комплексных бесконечногранников в $ℂ^{3}$ . Коксетер дал двенадцати из них символы $δ_{3}^{p, r}$ , где q ограничено выражением $q = 2 / (1 - (p + r) / p r)$ . Их можно разложить на произведение бесконечногранников: Шаблон:CDD = Шаблон:CDD. В первом случае имеем Шаблон:Не переведено 5 в $ℝ^{3}$ .

Ранг 4
Простран- ство	Группа	3-бесконечногранник	Рёбра	Грани	Ячейки	бесконечно- угольники ван Осса	Примечания
$ℂ^{3}$	_p[4]₂[3]₂[4]_r	$δ_{3}^{p, r} =_{p} {4}_{2} {3}_{2} {4}_{r}$ Шаблон:CDD	_p{}	$_{p} {4}_{2}$	$_{p} {4}_{2} {3}_{2}$	$_{p} {q}_{r}$	То же, что и Шаблон:CDD
$ℝ^{3}$	₂[4]₂[3]₂[4]₂ =[4,3,4]	$δ_{3}^{2, 2} =_{2} {4}_{2} {3}_{2} {4}_{2}$ Шаблон:CDD	{}	{4}	{4,3}		Шаблон:Не переведено 5 То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD
$ℂ^{3}$	$_{3} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{3, 2} =_{3} {4}_{2} {3}_{2} {4}_{2}$ Шаблон:CDD	₃{}	₃{4}₂	₃{4}₂{3}₂		То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD
$ℂ^{3}$	$_{3} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{2, 3} =_{2} {4}_{2} {3}_{2} {4}_{3}$ Шаблон:CDD	{}	{4}	{4,3}		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{3} [4]_{2} [3]_{2} [4]_{3}$	$δ_{3}^{3, 3} =_{3} {4}_{2} {3}_{2} {4}_{3}$ Шаблон:CDD	$_{3} {}$	$_{3} {4}_{2}$	$_{3} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{4} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{4, 2} =_{4} {4}_{2} {3}_{2} {4}_{2}$ Шаблон:CDD	$_{4} {}$	$_{4} {4}_{2}$	$_{4} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD
$ℂ^{3}$	$_{4} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{2, 4} =_{2} {4}_{2} {3}_{2} {4}_{4}$ Шаблон:CDD	{}	{4}	{4,3}		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{4} [4]_{2} [3]_{2} [4]_{4}$	$δ_{3}^{4, 4} =_{4} {4}_{2} {3}_{2} {4}_{4}$ Шаблон:CDD	₄{}	₄{4}₂	₄{4}₂{3}₂		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{6} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{6, 2} =_{6} {4}_{2} {3}_{2} {4}_{2}$ Шаблон:CDD	$_{6} {}$	$_{6} {4}_{2}$	$_{6} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD или Шаблон:CDD или Шаблон:CDD
$ℂ^{3}$	$_{6} [4]_{2} [3]_{2} [4]_{2}$	$δ_{3}^{2, 6} =_{2} {4}_{2} {3}_{2} {4}_{6}$ Шаблон:CDD	{}	{4}	{4,3}		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{6} [4]_{2} [3]_{2} [4]_{3}$	$δ_{3}^{6, 3} =_{6} {4}_{2} {3}_{2} {4}_{3}$ Шаблон:CDD	$_{6} {}$	$_{6} {4}_{2}$	$_{6} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD
$ℂ^{3}$	$_{6} [4]_{2} [3]_{2} [4]_{3}$	$δ_{3}^{3, 6} =_{3} {4}_{2} {3}_{2} {4}_{6}$ Шаблон:CDD	$_{3} {}$	$_{3} {4}_{2}$	$_{3} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD
$ℂ^{3}$	₆[4]₂[3]₂[4]₆	$δ_{3}^{6, 6} =_{6} {4}_{2} {3}_{2} {4}_{6}$ Шаблон:CDD	₆{}	$_{6} {4}_{2}$	$_{6} {4}_{2} {3}_{2}$		То же, что и Шаблон:CDD

Ранг 4, исключительные случаи
Простран- ство	Группа	3-бесконечногранник	Вершины	Рёбра	Грани	Ячейки	бесконечно- угольник ван Осса	Примечания
$ℂ^{3}$	$_{2} [4]_{3} [3]_{3} [3]_{3}$	$_{3} {3}_{3} {3}_{3} {4}_{2}$ Шаблон:CDD	1	24 $_{3} {}$	27 $_{3} {3}_{3}$	2 $_{3} {3}_{3} {3}_{3}$	$_{3} {4}_{6}$	То же, что и Шаблон:CDD
$ℂ^{3}$	$_{2} [4]_{3} [3]_{3} [3]_{3}$	$_{2} {4}_{3} {3}_{3} {3}_{3}$ Шаблон:CDD	2	27 {}	24 $_{2} {4}_{3}$	1 $_{2} {4}_{3} {3}_{3}$	$_{2} {12}_{3}$
$ℂ^{3}$	$_{2} [3]_{2} [4]_{3} [3]_{3}$	$_{2} {3}_{2} {4}_{3} {3}_{3}$ Шаблон:CDD	1	27 {}	72 $_{2} {3}_{2}$	8 $_{2} {3}_{2} {4}_{3}$	$_{2} {6}_{6}$
$ℂ^{3}$	$_{2} [3]_{2} [4]_{3} [3]_{3}$	$_{3} {3}_{3} {4}_{2} {3}_{2}$ Шаблон:CDD	8	72 $_{3} {}$	27 $_{3} {3}_{3}$	1 $_{3} {3}_{3} {4}_{2}$	$_{3} {6}_{3}$	То же, что и Шаблон:CDD или Шаблон:CDD

Правильные комплексные 4-бесконечногранники

Существует 15 правильных комплексных бесконечногранников в $ℂ^{4}$ . Коксетер дал двенадцати из них символы $δ_{4}^{p, r}$ , где q ограничено выражением $q = 2 / (1 - (p + r) / p r)$ . Они могут быть разложены в произведение бесконечногранников: Шаблон:CDD = Шаблон:CDD. В первом случае имеем в качестве вещественных решений Шаблон:Не переведено 5. Шаблон:Не переведено 5 и Шаблон:Не переведено 5 в $ℝ^{4}$ . Последнее решение имеет в качестве элементов Шаблон:Не переведено 5.

Ранг 5
Простран- ство	Группа	4-бесконечногранник	Вершины	Рёбра	Грани	Ячейки	4-грани	Бесконечно- угольник ван Осса	Примечания
$ℂ^{4}$	$_{p} [4]_{2} [3]_{2} [3]_{2} [4]_{r}$	$δ_{4}^{p, r} =_{p} {4}_{2} {3}_{2} {3}_{2} {4}_{r}$ Шаблон:CDD		$_{p} {}$	$_{p} {4}_{2}$	$_{p} {4}_{2} {3}_{2}$	$_{p} {4}_{2} {3}_{2} {3}_{2}$	$_{p} {q}_{r}$	То же, что и Шаблон:CDD
$ℝ^{4}$	$_{2} [4]_{2} [3]_{2} [3]_{2} [4]_{2}$	$δ_{4}^{2, 2} = {4, 3, 3, 3}$ Шаблон:CDD		{}	{4}	{4,3}	{4,3,3}	{∞}	Шаблон:Не переведено 5 То же, что и Шаблон:CDD
$ℝ^{4}$	$_{2} [3]_{2} [4]_{2} [3]_{2} [3]_{2}$ =[3,4,3,3]	{3,3,4,3} Шаблон:CDD	1	12 {}	32 {3}	24 {3,3}	3 {3,3,4}		Вещественные Шаблон:Не переведено 5 То же, что и Шаблон:CDD
$ℝ^{4}$	$_{2} [3]_{2} [4]_{2} [3]_{2} [3]_{2}$ =[3,4,3,3]	{3,4,3,3} Шаблон:CDD	3	24 {}	32 {3}	12 {3,4}	1 {3,4,3}		Вещественные Шаблон:Не переведено 5 То же, что и Шаблон:CDD или Шаблон:CDD
$ℂ^{4}$	$_{3} [3]_{3} [3]_{3} [3]_{3} [3]_{3}$	$_{3} {3}_{3} {3}_{3} {3}_{3} {3}_{3}$ Шаблон:CDD	1	80 $_{3} {}$	270 $_{3} {3}_{3}$	80 $_{3} {3}_{3} {3}_{3}$	1 $_{3} {3}_{3} {3}_{3} {3}_{3}$	$_{3} {4}_{6}$	$ℝ^{8}$ представление Шаблон:Не переведено 5

Правильные комплексные 5-бесконечногранники и выше

Существует только 12 правильных комплексных бесконечногранников в $ℂ^{5}$ и вышеШаблон:Sfn, которые обозначаются символами $δ_{n}^{p, r}$ , где q ограничено выражением $q = 2 / (1 - (p + r) / p r)$ . Их можно разложить на произведение n бесконечногранников: Шаблон:CDD … Шаблон:CDD = Шаблон:CDD … Шаблон:CDD. В первом случае имеем гиперкубические соты в $ℝ^{n}$ .

Ранг 6
Простран- ство	Группа	5-бесконечногранники	Вершины	Рёбра	Грани	Ячейки	4-грани	5-грани	Много- угольники ван Осса	Примечания
$ℂ^{5}$	$_{p} [4]_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{r}$	$δ_{5}^{p, r} =_{p} {4}_{2} {3}_{2} {3}_{2} {3}_{2} {4}_{r}$ Шаблон:CDD		$_{p} {}$	$_{p} {4}_{2}$	$_{p} {4}_{2} {3}_{2}$	$_{p} {4}_{2} {3}_{2} {3}_{2}$	$_{p} {4}_{2} {3}_{2} {3}_{2} {3}_{2}$	$_{p} {q}_{r}$	То же, что и Шаблон:CDD
$ℝ^{5}$	$_{2} [4]_{2} [3]_{2} [3]_{2} [3]_{2} [4]_{2}$ =[4,3,3,3,4]	$δ_{5}^{2, 2} = {4, 3, 3, 3, 4}$ Шаблон:CDD		{}	{4}	{4,3}	{4,3,3}	{4,3,3,3}	{∞}	Шаблон:Не переведено 5 То же, что и Шаблон:CDD

Многоугольники ван Осса

Многоугольник ван Осса является правильным многоугольником на плоскости (вещественной плоскости $ℝ^{2}$ или комплексной плоскости $ℂ^{2}$ ), в которой лежат как рёбра, так и барицентр правильного многогранника, и который образован элементами многогранника. Не все правильные многогранники имеют многоугольники ван Осса.

Например, многоугольники ван Осса вещественного октаэдра — это три квадрата, плоскости которых проходят через центр октаэдра. Для контраста, куб не имеет многоугольников ван Осса, поскольку плоскость от ребра к центру рассекает по диагонали две квадратные грани, так что два ребра куба на полученной плоскости не образуют многоугольника.

Бесконечные соты также имеют многоугольники ван Осса. Например, вещественная квадратная мозаика и треугольная мозаика имеют апейрогоны {∞} в качестве многоугольников ван ОссаШаблон:Sfn.

Многоугольник ван Осса правильного комплексного многогранника вида $_{p} {q}_{r} {s}_{t}$ …, если существует, имеет p-рёбер. Шаблон:Clear

Неправильные комплексные многогранники

Произведение комплексных многогранников

Пример произведения комплексных многогранников
Комплексное произведение многоугольников Шаблон:CDD или ${} \times_{5} {}$ , имеет 10 вершин, связанных пятью 2-рёбрами и двумя 5-рёбрами, и имеет представление как 3-мерная пятиугольная призма.	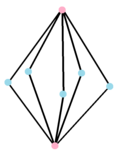Двойственный многоугольник ${} +_{5} {}$ , имеет 7 вершин, находящихся в середине исходных рёбер, соединённых 10 рёбрами. Его вещественным представлением является пятиугольная бипирамида.

Некоторые комплексные многогранники можно представить как прямое произведение. Эти произведения многогранников не являются строго правильными, поскольку имеют более одного типа фасет, но некоторые могут представить более низкие симметрии правильных форм, если все ортогональные многогранники одинаковы. Например, произведение $_{p} {} \times_{p} {}$ или Шаблон:CDD двух 1-мерных многогранников является тем же, что и правильный многогранник $_{p} {4}_{2}$ или Шаблон:CDD. Более общие произведения, наподобие $_{p} {} \times_{q} {}$ имеют вещественные представления как 4-мерные p-q дуопризмы. Двойственный многогранник произведения многогранников можно записать как сумму $_{p} {} +_{q} {}$ и он имеет вещественное представление как 4-мерная p-q Шаблон:Не переведено 5. Многогранник $_{p} {} +_{p} {}$ может иметь симметрию, удвоенную по сравнению с правильным комплексным многогранником $_{2} {4}_{p}$ или Шаблон:CDD.

Аналогично, комплексный многогранник $ℂ^{3}$ можно построить как тройное произведение: $_{p} {} \times_{p} {} \times_{p} {}$ или Шаблон:CDD — то же, что и правильный обобщённый куб, $_{p} {4}_{2} {3}_{2}$ или Шаблон:CDD, как и произведение $_{p} {4}_{2} \times_{p} {}$ или Шаблон:CDD Шаблон:Sfn.

Квазиправильные многогранники

Квазиправильный многоугольник является усечением правильного многоугольника. Квазиправильный многоугольник Шаблон:CDD содержит чередование рёбер правильных многоугольников Шаблон:CDD и Шаблон:CDD. Квазиправильный многоугольник имеет p вершин на p-рёбрах правильных видов.

Примеры квазиправильных многогранников
_p[q]_r	₂[4]₂	₃[4]₂	₄[4]₂	₅[4]₂	₆[4]₂	₇[4]₂	₈[4]₂	₃[3]₃	₃[4]₃
Правильный Шаблон:CDD	Шаблон:CDD 4 2-ребра	Шаблон:CDD 9 3-рёбер	Шаблон:CDD 16 4-рёбер	Шаблон:CDD 25 5-рёбер	Шаблон:CDD 36 6-рёбер	Шаблон:CDD 49 8-рёбер	Шаблон:CDD 64 8-ребра	Шаблон:CDD	Шаблон:CDD
Квази- правильный Шаблон:CDD	Шаблон:CDD = Шаблон:CDD 4+4 2-рёбер	Шаблон:CDD 6 2-рёбер 9 3-рёбер	Шаблон:CDD 8 2-рёбер 16 4-рёбер	Шаблон:CDD 10 2- рёбер 25 5-рёбер	Шаблон:CDD 12 2-рёбер 36 6-рёбер	Шаблон:CDD 14 2-рёбер 49 7-рёбер	Шаблон:CDD 16 2-рёбер 64 8-рёбер	Шаблон:CDD = Шаблон:CDD	Шаблон:CDD = Шаблон:CDD
Правильный Шаблон:CDD	Шаблон:CDD 4 2-ребра	Шаблон:CDD 6 2-рёбер	Шаблон:CDD 8 2-рёбер	Шаблон:CDD 10 2-рёбер	Шаблон:CDD 12 2-рёбер	Шаблон:CDD 14 2-рёбер	Шаблон:CDD 16 2-рёбер	Шаблон:CDD	Шаблон:CDD

Квазиправильные апейрогоны

Существует 7 квазиправильных комплексных бесконечноугольников, которые чередуют рёбра правильного бесконечноугольника и его двойственного. Шаблон:Не переведено 5 этого бесконечноугольника имеют представления с правильными и однородными мозаиками евклидовой плоскости. Последний столбец для 6{3}6 содержит бесконечноугольники, которые не только самодвойственны, но для них двойственный совпадает с собой с наложенными шестиугольными рёбрами, так что их квазирегулярные формы также имеют наложенные шестиугольные рёбра и он не может быть нарисован двумя чередующимися цветами, как в других столбцах. Симметрия самодвойственных семейств может быть удвоена, создавая тем самым идентичную геометрию, как в правильных формах: Шаблон:CDD = Шаблон:CDD

$_{p} [q]_{r}$	$_{4} [8]_{2}$	$_{4} [4]_{4}$	$_{6} [6]_{2}$	$_{6} [4]_{3}$	$_{3} [12]_{2}$	$_{3} [6]_{3}$	$_{6} [3]_{6}$
Правильный Шаблон:CDD или _p{q}_r	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD
Квазиправильный Шаблон:CDD	Шаблон:CDD	Шаблон:CDD = Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD = Шаблон:CDD	Шаблон:CDD = Шаблон:CDD
Правильный двойственный Шаблон:CDD или _r{q}_p	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD	Шаблон:CDD

Квазиправильные многоугольники

Как и в случае вещественных многогранников, комплексный квазиправильный многогранник может быть построен как полное усечение правильного многогранника. Вершины образуются в середине рёбер правильного многогранника, а грани правильного многогранника и их двойственные попеременно располагаются вдоль общих рёбер.

Например, p-обобщённый куб Шаблон:CDD,
имеет p³ вершин, 3p² рёбер и 3p p-обобщённых квадратных граней, в то время как p-обобщённый октаэдр Шаблон:CDD,
имеет 3p вершин, 3p² рёбер и p³ треугольных граней. Средняя квазиправильная форма p-обобщённого кубоктаэдра Шаблон:CDD,
имеет 3p² вершины, 3p³ рёбер и 3p+p³ граней.

Также полное усечение Шаблон:Не переведено 5 Шаблон:CDD — это Шаблон:CDD, квазиправильная форма, разделяющая геометрию правильного комплексного многогранника Шаблон:CDD.

Квазиправильные примеры
Обобщённый куб/октаэдр						Шаблон:Не переведено 5
	p=2 (вещ.)	p=3	p=4	p=5	p=6	Шаблон:Не переведено 5
Обобщённые кубы Шаблон:CDD (правильный)	Куб, Шаблон:CDD, 8 вершин, 12 2-рёбер и 6 граней.	Шаблон:CDD, 27 вершин, 27 3-рёбер и 9 граней, по одной Шаблон:CDD грани (синяя и красная)	Шаблон:CDD, 64 вершины, 48 4-рёбер и 12 граней.	Шаблон:CDD, 125 вершин, 75 5-рёбер и 15 граней.	Шаблон:CDD, 216 вершин, 108 6-рёбер и 18 граней.	Шаблон:CDD, 27 вершин, 72 6-ребра и 27 граней.
Обобщённый кубоктаэдр Шаблон:CDD (квазиправильный)	Кубооктаэдр Шаблон:CDD, 12 вершин, 24 2-ребра и 6+8 граней.	Шаблон:CDD, 27 вершин, 81 2-ребро и 9+27 граней, одна Шаблон:CDD грань (синяя)	Шаблон:CDD, 48 вершин, 192 2-ребра и 12+64 грани, одна Шаблон:CDD грань (синяя)	Шаблон:CDD, 75 вершин, 375 2-рёбер и 15+125 граней.	Шаблон:CDD, 108 вершин, 648 2-рёбер и 18+216 граней.	Шаблон:CDD = Шаблон:CDD, 72 вершины, 216 3-рёбер и 54 грани.
Обобщённый октаэдр Шаблон:CDD (правильный)	Октаэдр Шаблон:CDD, 6 вершин, 12 2-рёбер и 8 {3} граней.	Шаблон:CDD, 9 вершин, 27 2-рёбер и 27 {3} граней.	Шаблон:CDD, 12 вершин, 48 2-рёбер и 64 {3} грани.	Шаблон:CDD, 15 вершин, 75 2-рёбер и 125 {3} граней.	Шаблон:CDD, 18 вершин, 108 2-рёбер и 216 {3} граней.	Шаблон:CDD, 27 вершин, 72 6-ребра и 27 граней.

Другие комплексные многогранники с комплексными отражениями периода два

Другие неправильные комплексные многогранники могут быть построены с помощью комплексных групп отражений, которые не дают линейных графов Коксетера. В диаграммах Коксетера с петлями Коксетер отмечает период, как в диаграмме Шаблон:CDD или символе $(1_{1} 1 1)^{3}$ и группе $[1 1 1]^{3}$ Шаблон:Sfn Шаблон:Sfn. Эти комплексные многогранники не исследованы систематически за пределами нескольких частных случаев.

Группа Шаблон:CDD определяется 3 комплексными отражениями, $R_{1}, R_{2}, R_{3}$ , все порядка 2: $R_{1}^{2} = R_{1}^{2} = R_{3}^{2} = (R_{1} R_{2})^{3} = (R_{2} R_{3})^{3} = (R_{3} R_{1})^{3} = (R_{1} R_{2} R_{3} R_{1})^{p} = 1$ . Период p можно рассматривать как двойное вращение в вещественном пространстве $ℝ^{4}$ .

Как и в случае построений Витхоффа, для многогранников, генерируемых отражениями, число вершин многогранника, имеющего диаграмму Коксетера с одним кружком, равно порядку группы, разделённой на порядок подгруппы, в которой обведённый узел удалён. Например, вещественный куб имеет диаграмму Коксетера Шаблон:CDD, с Шаблон:Не переведено 5 Шаблон:CDD порядка 48 и подгруппу диэдральной симметрии Шаблон:CDD порядка 6, так что число вершин куба равно s 48/6=8. Фасеты строятся путём удаления одного узла, самого удалённого от узла с кружком, например Шаблон:CDD для куба. Вершинные фигуры генерируются путём удаления обведённого узла и помещения кружка или кружков на соседние узлы, Шаблон:CDD для куба.

Коксетер представляет эти группы следующими символами. Некоторые группу имеют одинаковый порядок, но различную структуру, определяя то же Шаблон:Не переведено 5 в комплексных многогранниках, но различные рёбра и элементы более высокой размерности, как в диаграммах Шаблон:CDD и Шаблон:CDD с p≠3Шаблон:Sfn

Группы, генерируемые комплексными отражениями
Диаграмма Коксетера	Порядок	Символ или положение в таблицеVII Шепарда или Тодда (1954)
Шаблон:CDD, (Шаблон:CDD и Шаблон:CDD), Шаблон:CDD, Шаблон:CDD …	p^{n − 1} n!, p ≥ 3	$G (p, p, n), [p], [1 1 1]^{p}, [1 1 (n - 2)^{p}]^{3}$
Шаблон:CDD, Шаблон:CDD	72•6!, 108•9!	№ 33, 34, $[1 2 2]^{3}$ , $[1 2 3]^{3}$
Шаблон:CDD, (Шаблон:CDD и Шаблон:CDD), (Шаблон:CDD и Шаблон:CDD)	14•4!, 3•6!, 64•5!	№ 24, 27, 29

Коксетер называет некоторые из этих комплексных многогранников почти правильными, поскольку они имеют правильные фасеты и вершинные фигуры. Первый является вариантом обобщённого кросс-многогранника с меньшей симметрией в $ℂ^{3}$ . Второй является дробным обобщённым кубом, в котором p-рёбра сведены в отдельные вершины, оставляя простые 2-рёбра. Три из них связаны с конечным правильным косым многогранником в $ℝ^{4}$ .

Некоторые почти правильные комплексные многогранникиШаблон:Sfn
Простран ство	Группа	Порядок	Символы Коксетера	Вершины	Рёбра	Грани	Вершинная фигура	Примечания
$ℂ^{3}$	$[1 1 1^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$6 p^{2}$	$(1 1 1_{1}^{p})^{3}$ Шаблон:CDD	3p	3p²	{3}	{2p}	Символ Шепарда $(1 1; 1_{1})^{p}$ то же, что и $β_{3}^{p} =$ Шаблон:CDD
$ℂ^{3}$	$[1 1 1^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$6 p^{2}$	$(1_{1} 1 1^{p})^{3}$ Шаблон:CDD	p²		{3}	{6}	Символ Шепарда $(1_{1} 1; 1)^{p}$ $1 / p γ_{3}^{p}$
$ℝ^{3}$	$[1 1 1^{2}]^{3}$ Шаблон:CDD	24	$(1 1 1_{1}^{2})^{3}$ Шаблон:CDD	6	12	8 {3}	{4}	То же, что и $β_{3}^{2} =$ Шаблон:CDD = вещественный октаэдр
$ℝ^{3}$	$[1 1 1^{2}]^{3}$ Шаблон:CDD	24	$(1_{1} 1 1^{2})^{3}$ Шаблон:CDD	4	6	4 {3}	{3}	1/2 $γ_{3}^{2} =$ Шаблон:CDD = $α_{3}$ = вещественный тетраэдр
$ℂ^{3}$	$[1 1 1]^{3}$ Шаблон:CDD	54	$(1 1 1_{1})^{3}$ Шаблон:CDD	9	27	{3}	{6}	Символ Шепарда $(1 1; 1_{1})^{3}$ то же, что и $β_{3}^{3} =$ Шаблон:CDD
$ℂ^{3}$	$[1 1 1]^{3}$ Шаблон:CDD	54	$(1_{1} 1 1)^{3}$ Шаблон:CDD	9	27	{3}	{6}	Символ Шепарда $(1_{1} 1; 1)^{3}$ 1/3 $γ_{3}^{3} = β_{3}^{3}$
$ℂ^{3}$	$[1 1 1^{4}]^{3}$ Шаблон:CDD	96	$(1 1 1_{1}^{4})^{3}$ Шаблон:CDD	12	48	{3}	{8}	Символ Шепарда $(1 1; 1_{1})^{4}$ то же, что и $β_{3}^{4} =$ Шаблон:CDD
$ℂ^{3}$	$[1 1 1^{4}]^{3}$ Шаблон:CDD	96	$(1_{1} 1 1^{4})^{3}$ Шаблон:CDD	16		{3}	{6}	Символ Шепарда $(1_{1} 1; 1)^{4}$ 1/4 $γ_{3}^{4}$
$ℂ^{3}$	$[1 1 1^{5}]^{3}$ Шаблон:CDD	150	$(1 1 1_{1}^{5})^{3}$ Шаблон:CDD	15	75	{3}	{10}	Символ Шепарда $(1 1; 1_{1})^{5}$ то же, что и $β_{3}^{5} =$ Шаблон:CDD
$ℂ^{3}$	$[1 1 1^{5}]^{3}$ Шаблон:CDD	150	$(1_{1} 1 1^{5})^{3}$ Шаблон:CDD	25		{3}	{6}	Символ Шепарда $(1_{1} 1; 1)^{5}$ 1/5 $γ_{3}^{5}$
$ℂ^{3}$	$[1 1 1^{6}]^{3}$ Шаблон:CDD	216	$(1 1 1_{1}^{6})^{3}$ Шаблон:CDD	18	216	{3}	{12}	Символ Шепарда $(1 1; 1_{1})^{6}$ то же, что и $β_{3}^{6} =$ Шаблон:CDD
$ℂ^{3}$	$[1 1 1^{6}]^{3}$ Шаблон:CDD	216	$(1_{1} 1 1^{6})^{3}$ Шаблон:CDD	36		{3}	{6}	Символ Шепарда $(1_{1} 1; 1)^{6}$ 1/6 $γ_{3}^{6}$
$ℂ^{3}$	$[1 1 1^{4}]^{4}$ Шаблон:CDD	336	$(1 1 1 {_{1}}^{4})^{4}$ Шаблон:CDD	42	168	112 {3}	{8}	$ℝ^{4}$ представление {3,8\|,4} = {3,8}₈
$ℂ^{3}$	$[1 1 1^{4}]^{4}$ Шаблон:CDD	336	$(1_{1} 1 1^{4})^{4}$ Шаблон:CDD	56		{3}	{6}
$ℂ^{3}$	$[1 1 1_{5}]^{4}$ Шаблон:CDD	2160	$(1 1 1_{1}^{5})^{4}$ Шаблон:CDD	216	1080	720 {3}	{10}	$ℝ^{4}$ представление ${3, 10 ∣, 4} = {3, 10}_{8}$
$ℂ^{3}$	$[1 1 1_{5}]^{4}$ Шаблон:CDD		$(1_{1} 1 1^{5})^{4}$ Шаблон:CDD	360		{3}	{6}
$ℂ^{3}$	$[1 1 1^{4}]^{5}$ Шаблон:CDD		$(1 1 1_{1}^{4})^{5}$ Шаблон:CDD	270	1080	720 {3}	{8}	$ℝ^{4}$ представление ${3, 8 ∣, 5} = {3, 8}_{10}$
$ℂ^{3}$	$[1 1 1^{4}]^{5}$ Шаблон:CDD		$(1_{1} 1 1^{4})^{5}$ Шаблон:CDD	360		{3}	{6}

Коксетер определил и другие группы с антиунитарным построением, например, эти три. Первая группа была открыта и нарисована Шаблон:Не переведено 5 в 1966Шаблон:Sfn

Некоторые другие почти правильные комплексные многогранникиШаблон:Sfn
Простран ство	Группа	Порядок	Символы Коксетера	Вершины	Рёбра	Грани	Вершинная фигура	Примечания
$ℂ^{3}$	$[1 1^{4} 1^{4}]^{(3)}$ Шаблон:CDD	336	$(1_{1} 1^{4} 1^{4})^{(3)}$ Шаблон:CDD	56	168	84 {4}	{6}	$ℝ^{4}$ представление ${4, 6 ∣, 3} = {4, 6}_{6}$
$ℂ^{3}$	$[1^{5} 1^{4} 1^{4}]^{(3)}$ Шаблон:CDD	2160	$(1_{1}^{5} 1^{4} 1^{4})^{(3)}$ Шаблон:CDD	216	1080	540 {4}	{10}	$ℝ^{4}$ представление ${4, 10 ∣, 3} = {4, 10}_{6}$
$ℂ^{3}$	$[1^{4} 1^{5} 1^{5}]^{(3)}$ Шаблон:CDD	2160	$(1_{1}^{4} 1^{5} 1^{5})^{(3)}$ Шаблон:CDD	270	1080	432 {5}	{8}	$ℝ^{4}$ представление ${5, 8 ∣, 3} = {5, 8}_{6}$

Некоторые комплексные 4-многогранникиШаблон:Sfn
Простран ство	Группа	Порядок	Символы Коксетера	Вершины	Другие элементы	Ячейки	Вершинная фигура	Примечания
$ℂ^{4}$	$[1 1 2^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$24 p^{3}$	$(1 1 2_{2}^{p})^{3}$ Шаблон:CDD	4p		Шаблон:CDD	Шаблон:CDD	Шепард $(2_{2} 1; 1)^{p}$ то же, что и $β_{4}^{p} =$ Шаблон:CDD
$ℂ^{4}$	$[1 1 2^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$24 p^{3}$	$(1_{1} 1 2^{p})^{3}$ Шаблон:CDD	$p^{3}$		Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 1_{1})^{p}$ $1 / p γ_{4}^{p}$
$ℝ^{4}$	$[1 1 2^{2}]^{3}$ $= [3^{1, 1, 1}]$ Шаблон:CDD	192	$(1 1 2_{2}^{2})^{3}$ Шаблон:CDD	8	24 ребра 32 грани	16 Шаблон:CDD	Шаблон:CDD	$β_{4}^{2} =$ Шаблон:CDD, вещественный шестнадцатиячейник
$ℝ^{4}$	$[1 1 2^{2}]^{3}$ $= [3^{1, 1, 1}]$ Шаблон:CDD	192	$(1_{1} 1 2^{2})^{3}$ Шаблон:CDD	8	24 ребра 32 грани	16 Шаблон:CDD	Шаблон:CDD	1/2 $γ_{4}^{2} =$ Шаблон:CDD = $β_{4}^{2}$ , вещественный шестнадцатиячейник
$ℂ^{4}$	$[1 1 2]^{3}$ Шаблон:CDD	648	$(1 1 2_{2})^{3}$ Шаблон:CDD	12		Шаблон:CDD	Шаблон:CDD	Шепард $(2_{2} 1; 1)^{3}$ то же, что и $β_{4}^{3} =$ Шаблон:CDD
$ℂ^{4}$	$[1 1 2]^{3}$ Шаблон:CDD	648	$(1_{1} 1 2^{3})^{3}$ Шаблон:CDD	27		Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 1_{1})^{3}$ $1 / 3 γ_{4}^{3}$
$ℂ^{4}$	$[1 1 2^{4}]^{3}$ Шаблон:CDD	1536	$(1 1 2_{2}^{4})^{3}$ Шаблон:CDD	16		Шаблон:CDD	Шаблон:CDD	Шепард $(2_{2} 1; 1)^{4}$ то же, что и $β_{4}^{4} =$ Шаблон:CDD
$ℂ^{4}$	$[1 1 2^{4}]^{3}$ Шаблон:CDD	1536	$(1_{1} 1 2^{4})^{3}$ Шаблон:CDD	64		Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 1_{1})^{4}$ $1 / 4 γ_{4}^{4}$
$ℂ^{4}$	$[1^{4} 1 2]^{3}$ Шаблон:CDD	7680	$(2_{2} 1^{4} 1)^{3}$ Шаблон:CDD	80		Шаблон:CDD	Шаблон:CDD	Шепард $(2_{2} 1; 1)^{4}$
			$(1_{1}^{4} 1 2)^{3}$ Шаблон:CDD	160		Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 1_{1})^{4}$
			(1₁ 1⁴ 2)³ Шаблон:CDD	320		Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1_{1}; 1)^{4}$
$ℂ^{4}$	$[1 1 2]^{4}$ Шаблон:CDD		$(1 1 2_{2})^{4}$ Шаблон:CDD	80	640 рёбер 1280 треугольников	640 Шаблон:CDD	Шаблон:CDD
$ℂ^{4}$	$[1 1 2]^{4}$ Шаблон:CDD		$(1_{1} 1 2)^{4}$ Шаблон:CDD	320		Шаблон:CDD Шаблон:CDD	Шаблон:CDD

Некоторые комплексные 5-многогранникиШаблон:Sfn
Простран ство	Группа	Порядок	Символы Коксетера	Вершины	Фасеты	Вершинная фигура	Примечания
$ℂ^{5}$	$[1 1 3^{p}]^{3}$ Шаблон:CDD p=2,3,4…	120p⁴	$(1 1 3_{3}^{p})^{3}$ Шаблон:CDD	5p	Шаблон:CDD	Шаблон:CDD	Шепард $(3_{3} 1; 1)^{p}$ то же, что и $β_{5}^{p} =$ Шаблон:CDD
$ℂ^{5}$	$[1 1 3^{p}]^{3}$ Шаблон:CDD p=2,3,4…	120p⁴	$(1_{1} 1 3^{p})^{3}$ Шаблон:CDD	$p^{4}$	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(3 1; 1_{1})^{p}$ 1/p γШаблон:Supsub
$ℂ^{5}$	$[2 2 1]^{3}$ Шаблон:CDD	51840	$(2 1 2_{2})^{3}$ Шаблон:CDD	80	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 2_{2})^{3}$
$ℂ^{5}$	$[2 2 1]^{3}$ Шаблон:CDD	51840	$(2 1_{1} 2)^{3}$ Шаблон:CDD	432	Шаблон:CDD	Шаблон:CDD	Шепард $(2 1_{1}; 2)^{3}$

Некоторые комплексные 6-многогранникиШаблон:Sfn
Простран ство	Группа	Порядок	Символы Коксетера	Вершины	Фасеты	Вершинная фигура	Примечания
$ℂ^{6}$	$[1 1 4^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$720 p^{5}$	$(1 1 4_{4}^{p})^{3}$ Шаблон:CDD	6p	Шаблон:CDD	Шаблон:CDD	Шепард $(4_{4} 1; 1)^{p}$ то же, что и $β_{6}^{p} =$ Шаблон:CDD
$ℂ^{6}$	$[1 1 4^{p}]^{3}$ Шаблон:CDD p=2,3,4…	$720 p^{5}$	$(1_{1} 1 4^{p})^{3}$ Шаблон:CDD	$p^{5}$	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(41; 1_{1})^{p}$ $1 / p γ_{6}^{p}$
$ℂ^{6}$	$[1 2 3]^{3}$ Шаблон:CDD	39191040	$(2 1 3_{3})^{3}$ Шаблон:CDD	756	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1; 3_{3})^{3}$
			$(2_{2} 13)^{3}$ Шаблон:CDD	4032	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2_{2} 1; 3)^{3}$
			$(2 1_{1} 3)^{3}$ Шаблон:CDD	54432	Шаблон:CDD Шаблон:CDD	Шаблон:CDD	Шепард $(2 1_{1}; 3)^{3}$

Визуализация

$(1 1 1_{1}^{4})^{4}$ , Шаблон:CDD,
имеет 42 вершин, 168 рёбер и 112 треугольных граней, которые видны на этой 14-угольной проекции.
$(1^{4} 1^{4} 1_{1})^{(3)}$ , Шаблон:CDD,
имеет 56 вершин, 168 рёбер и 84 квадратных граней, которые видны на этой 14-угольной проекции.
$(1 1 2_{2})^{4}$ , Шаблон:CDD,
имеет 80 вершин, 640 рёбер, 1280 треугольных граней и 640 тетраэдральных ячеек, которые видны на этой 20-угольной проекцииШаблон:Sfn.

Примечания

Шаблон:Примечания

Литература

Литература для дальнейшего чтения

Шаблон:Книга

Шаблон:Rq

↑ Шаблон:Sfn0, простой h-угольник, образованный орбитой флага ( $O_{0}, O_{0} O_{1}$ ) для произведения двух генерирующих отражений любого незвёздного правильного комплексного многоугольника, $p_{1} {q} p_{2}$ .
↑ Shephard 1952; «Из соглашений, которые мы используем для определения понятия внутренности многогранника, видим, что в унитарном пространстве, где числа не могут быть упорядочены, понятие внутренности определить невозможно.
Поэтому … нам следует рассматривать унитарные многогранник как конфигурации.»

[1] Шаблон:Sfn0, простой h-угольник, образованный орбитой флага ( $O_{0}, O_{0} O_{1}$ ) для произведения двух генерирующих отражений любого незвёздного правильного комплексного многоугольника, $p_{1} {q} p_{2}$ .

[2] Shephard 1952; «Из соглашений, которые мы используем для определения понятия внутренности многогранника, видим, что в унитарном пространстве, где числа не могут быть упорядочены, понятие внутренности определить невозможно.
Поэтому … нам следует рассматривать унитарные многогранник как конфигурации.»

[1]

[2]

Комплексный многогранник

Содержание

Определение и вводные замечания

Правильные комплексные одномерные многогранники

Правильные комплексные многоугольники

Обозначения

Модифицированные Шепардом обозначения Шлефли

Пересмотренная нотация Шлефли

Диаграммы Коксетера — Дынкина

Перечисление правильных многоугольников

Визуализация правильных комплексных многоугольников

Правильные комплексные многогранники

Перечисление правильных комплексных многогранников

Визуализация правильных комплексных многогранников

Перечисление правильных комплексных 4-многогранников

Визуализация правильных комплексных 4-многогранников

Перечисление правильных комплексных 5-многогранников

Визуализация правильных комплексных 5-многогранников

Перечисление правильных комплексных 6-многогранников

Визуализация правильных комплексных 6-многогранников

Перечисление правильных комплексных бесконечногранников

Правильные комплексные 1-многогранники

Правильные комплексные апейрогоны

Правильные комплексные бесконечногранники (трёхмерное пространство)

Правильные комплексные 3-бесконечногранники

Правильные комплексные 4-бесконечногранники

Правильные комплексные 5-бесконечногранники и выше

Многоугольники ван Осса

Неправильные комплексные многогранники

Произведение комплексных многогранников

Квазиправильные многогранники

Квазиправильные апейрогоны

Квазиправильные многоугольники

Другие комплексные многогранники с комплексными отражениями периода два

Визуализация

Примечания

Литература

Литература для дальнейшего чтения

Навигация

Комплексный многогранник

Определение и вводные замечания

Правильные комплексные одномерные многогранники

Правильные комплексные многоугольники

Обозначения

Модифицированные Шепардом обозначения Шлефли

Пересмотренная нотация Шлефли

Диаграммы Коксетера — Дынкина

Перечисление правильных многоугольников

Визуализация правильных комплексных многоугольников

Правильные комплексные многогранники

Перечисление правильных комплексных многогранников

Визуализация правильных комплексных многогранников

Перечисление правильных комплексных 4-многогранников

Визуализация правильных комплексных 4-многогранников

Перечисление правильных комплексных 5-многогранников

Визуализация правильных комплексных 5-многогранников

Перечисление правильных комплексных 6-многогранников

Визуализация правильных комплексных 6-многогранников

Перечисление правильных комплексных бесконечногранников

Правильные комплексные 1-многогранники

Правильные комплексные апейрогоны

Правильные комплексные бесконечногранники (трёхмерное пространство)

Правильные комплексные 3-бесконечногранники

Правильные комплексные 4-бесконечногранники

Правильные комплексные 5-бесконечногранники и выше

Многоугольники ван Осса

Неправильные комплексные многогранники

Произведение комплексных многогранников

Квазиправильные многогранники

Квазиправильные апейрогоны

Квазиправильные многоугольники

Другие комплексные многогранники с комплексными отражениями периода два

Визуализация

Примечания

Литература

Литература для дальнейшего чтения

Навигация

Поиск