Момент инерции
Шаблон:Дзт Шаблон:Физическая величина Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: Шаблон:Math или Шаблон:Math.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Шаблон:Math, равная сумме произведений масс всех Шаблон:Math материальных точек системы на квадраты их расстояний до оси[1]:
где:
- Шаблон:Math — масса Шаблон:Math-й точки,
- Шаблон:Math — расстояние от Шаблон:Math-й точки до оси.
Осевой момент инерции тела Шаблон:Math является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
- Шаблон:Math — масса малого элемента объёма тела Шаблон:Math,
- Шаблон:Math — плотность,
- Шаблон:Math — расстояние от элемента Шаблон:Math до оси Шаблон:Math.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела Шаблон:Math относительно произвольной оси равен сумме момента инерции этого тела Шаблон:Math относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела Шаблон:Math на квадрат расстояния Шаблон:Math между осями[1]:
где Шаблон:Math — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
| Тело | Описание | Положение оси Шаблон:Math | Момент инерции Шаблон:Math |
|---|---|---|---|
| Материальная точка массы Шаблон:Math | На расстоянии Шаблон:Math от точки, неподвижная | ||

|
Полый тонкостенный цилиндр или кольцо радиуса Шаблон:Math и массы Шаблон:Math | Ось цилиндра | |

|
Сплошной цилиндр или диск радиуса Шаблон:Math и массы Шаблон:Math | Ось цилиндра | |

|
Полый толстостенный цилиндр массы Шаблон:Math с внешним радиусом Шаблон:Math и внутренним радиусом Шаблон:Math | Ось цилиндра | Шаблон:Ref+ |

|
Сплошной цилиндр длины Шаблон:Math, радиуса Шаблон:Math и массы Шаблон:Math | Ось перпендикулярна образующей цилиндра и проходит через его центр масс | |

|
Полый тонкостенный цилиндр (кольцо) длины Шаблон:Math, радиуса Шаблон:Math и массы Шаблон:Math | Ось перпендикулярна к цилиндру и проходит через его центр масс | |

|
Прямой тонкий стержень длины Шаблон:Math и массы Шаблон:Math | Ось перпендикулярна к стержню и проходит через его центр масс | |
|
Прямой тонкий стержень длины Шаблон:Math и массы Шаблон:Math | Ось перпендикулярна к стержню и проходит через его конец | |

|
Тонкостенная сфера радиуса Шаблон:Math и массы Шаблон:Math | Ось проходит через центр сферы | |

|
Шар радиуса Шаблон:Math и массы Шаблон:Math | Ось проходит через центр шара | |

|
Конус радиуса Шаблон:Math и массы Шаблон:Math | Ось конуса | |
| Равнобедренный треугольник с высотой Шаблон:Math, основанием Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте) | ||
| Правильный треугольник (сплошной) со стороной Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
| Квадрат (сплошной) со стороной Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости квадрата и проходит через центр масс | ||
| Прямоугольник (сплошной) со сторонами Шаблон:Math и Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости прямоугольника и проходит через центр масс | ||
| Правильный n-угольник (сплошной) с радиусом описанной окружности Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости и проходит через центр масс | ||
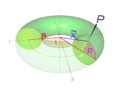
|
Тор (полый) с радиусом направляющей окружности Шаблон:Math, радиусом образующей окружности Шаблон:Math и массой Шаблон:Math | Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс |
Вывод формул
Тонкостенный цилиндр (кольцо, обруч) Шаблон:Hider Толстостенный цилиндр (кольцо, обруч) Шаблон:Hider
Однородный диск (сплошной цилиндр) Шаблон:Hider
Сплошной конус Шаблон:Hider
Сплошной однородный шар Шаблон:Hider
Тонкостенная сфера Шаблон:Hider
Тонкий стержень (ось проходит через центр) Шаблон:Hider
Тонкий стержень (ось проходит через конец) Шаблон:Hider
Безразмерные моменты инерции планет и спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса Шаблон:Math и массы Шаблон:Math равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии Шаблон:Math (равному Шаблон:Math). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[2][3].
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][4]:
где Шаблон:Math, Шаблон:Math и Шаблон:Math — координаты малого элемента тела объёмом Шаблон:Math, плотностью Шаблон:Math и массой Шаблон:Math.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Шаблон:Math и Шаблон:Math одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке Шаблон:Math тела, называются главными моментами инерции данного тела[4].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[4].
Геометрические моменты инерции
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[5]:
где, как и ранее Шаблон:Math — расстояние от элемента Шаблон:Math до оси Шаблон:Math.
Размерность Шаблон:Math — длина в пятой степени (), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[5]:
где интегрирование выполняется по поверхности Шаблон:Math, а Шаблон:Math — элемент этой поверхности.
Размерность Шаблон:Math — длина в четвёртой степени (), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
Здесь Шаблон:Math — максимальное расстояние от поверхности до оси.
| Геометрические моменты инерции площади некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : |
|
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно |
|
| Круга диаметром | |
Момент инерции относительно плоскости
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[6].
Если через произвольную точку провести координатные оси , то моменты инерции относительно координатных плоскостей , и будут выражаться формулами:
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) — это величина, определяемая выражением[6]:
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до точки O.
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[6]:
Тензор инерции и эллипсоид инерции
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1)
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
- Кинематика твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Теорема Кёнига (механика)
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
- Момент силы
- Момент импульса
Комментарии
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Шаблон:Wayback Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.