Экспоненциал

Экспоненциал — теоретико-категорный аналог множества функций в теории множеств. Категории, в которых существуют конечные пределы и экспоненциалы, называются декартово замкнутыми.

Определение

Пусть в категории $C$ существуют бинарные произведения. Тогда экспоненциал $Z^{Y}$ можно определить как универсальный морфизм из функтора $[-] \times Y$ в $Z$ . (Функтор $[-] \times Y$ из $C$ в $C$ отображает объект $X$ в $X \times Y$ и морфизмы $φ$ в $φ \times {i d}_{Y}$ ).

Более явно, экспоненциал $Z^{Y}$ объектов $Z$ и $Y$ — это такой объект, вместе с морфизмом $e v a l : Z^{Y} \times Y \to Z$ , называемым отображением оценки, что для любого объекта $X$ и морфизма $g : X \times Y \to Z$ существует единственный морфизм $λ g : X \to Z^{Y}$ , для которого следующая диаграмма коммутативна:

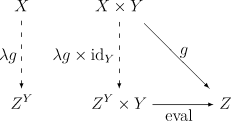
Universal property of the exponential object

Если экспоненциал $Z^{Y}$ существует для всех $Z$ в $C$ , то функтор, отправляющий $Z$ в $Z^{Y}$ является правым сопряжённым к $[-] \times Y$ . В этом случае существует естественная биекция:

H o m (X \times Y, Z) ≅ H o m (X, Z^{Y})

.

Примеры

В категории множеств экспоненциал $Z^{Y}$ — это множество всех функций из $Y$ в $Z$ (кардинальная степень). Для любого отображения $g : (X \times Y) \to Z$ отображение $λ g : X \to Z^{Y}$ — это каррированная форма $g$ :

λ g (x) (y) = g (x, y)

.

В категории топологических пространств экспоненциал $Z^{Y}$ существует, если $Y$ — локально компактное хаусдорфово пространство. В этом случае $Z^{Y}$ — это множество непрерывных функций из $Y$ в $Z$ с компактно-открытой топологией. Если $Y$ не локально компактное хаусдорфово пространство, экспоненциал может не существовать (пространство $Z^{Y}$ будет существовать, но отображение $λ$ может перестать быть непрерывным). По этой причине категория топологических пространств не является декартово замкнутой.

Литература

Экспоненциал

Определение

Примеры

Литература

Навигация

Поиск