Файл:Hajos construction.svg
Перейти к навигации
Перейти к поиску
Размер этого PNG-превью для исходного SVG-файла: 240 × 147 пкс. Другие разрешения: 320 × 196 пкс | 640 × 392 пкс | 1024 × 627 пкс | 1280 × 784 пкс | 2560 × 1568 пкс.
Исходный файл (SVG-файл, номинально 240 × 147 пкс, размер файла: 2 КБ)
Краткое описание
| Описание |
English: The Hajós construction, a method of combining pairs of graphs to produce a larger graph. If both of the smaller graphs require at least k colors in any coloring, then so does the larger graph. In this example, the two smaller graphs being combined are both copies of the complete graph K4, and the graph resulting from the combination is the Moser spindle. |
| Дата | |
| Источник | Собственная работа |
| Автор | David Eppstein |
Лицензирование
Я, владелец авторских прав на это произведение, добровольно публикую его на условиях следующей лицензии:
 
|
Этот файл доступен на условиях Creative Commons CC0 1.0 Универсальной передачи в общественное достояние (Universal Public Domain Dedication). |
| Лица, связанные с работой над этим произведением, решили передать данное произведение в общественное достояние, отказавшись от всех прав на произведение по всему миру в рамках закона об авторских правах (а также связанных и смежных прав), в той степени, которую допускает закон. Вы можете копировать, изменять, распространять и исполнять данное произведение в любых целях, в том числе в коммерческих, без получения на это разрешения автора.
|
История файла
Нажмите на дату/время, чтобы увидеть версию файла от того времени.
| Дата/время | Миниатюра | Размеры | Участник | Примечание | |
|---|---|---|---|---|---|
| текущий | 01:31, 22 июля 2011 | 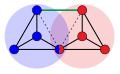| 240 × 147 (2 КБ) | wikimediacommons>David Eppstein | {{Information |Description ={{en|1=The en:Hajós construction, a method of combining pairs of graphs to produce a larger graph. If both of the smaller graphs require at least ''k'' colors in any coloring, then so does the larger graph. In this exa |
Использование файла
Следующая страница использует этот файл:
