Каноническая форма Вейра

Пример общей матрицы Вейра, состоящей из двух блоков, каждый из которых элементарная матрица Вейра. Одна элементарная матрица в верхнем левом углу имеет структуру (4,2,1), а другая (2,2,1,1).

Каноническая форма Вейра (форма Вейра, матрица Вейра, модифицированная форма Жордана, переупорядоченная форма Жордана, вторая форма Жордана, H-форма) — квадратная матрица удовлетворяющая определённым условиям, введена чешским математиком Шаблон:Нп2 в 1885 году.

Форма не получила широкого распространения в математических исследованиях, так как вместо неё использовалась близкая по предназначению, но отличная от неё каноническая форма Жордана, в связи с малой известностью форма переоткрывалась несколько раз. Известность форма приобрела в конце 1990-х — начале 2000-х годов в связи с применением в биоинформатике для филогенетических инвариантов.

Определения

Элементарная матрица Вейра

Элементарная матрица Вейра с собственным значением $\lambda$ это $n\times n$ матрица $W$ следующего вида:

Пусть задано разбиение

$n_1+n_2+\cdots +n_r=n$ числа $n$, где $n_1⩾n_2⩾\cdots ⩾n_r⩾1$ такое, что, когда $W$ рассматривается как блочная $r\times r$-матрица $(W_{ij})$, где $(i,j)$-й блок $W_{ij}$ представляет собой матрицу $n_i\times n_j$, причём выполнены следующие три условия:

1. Блоки главной диагонали $W_{ii}$ являются $n_i\times n_i$-скалярными матрицами $\lambda I$, где $i=1,\dots ,r$.
2. Блоки первой наддиагонали $W_{i,i+1}$ являются $n_i\times n_{i+1}$-матрицы полного столбцового ранга, имеющая ступенчатый вид по строкам (то есть единичная матрица, за которой следуют нулевые строки), где $i=1,\dots ,r-1$.
3. Все остальные блоки матрицы $W$ являются нулевыми (то есть $W_{ij}=0$, где $j\ne i,i+1$).

В данном случае говорят, что $W$ имеет структуру Вейра $(n_1,n_2,\dots ,n_r)$.

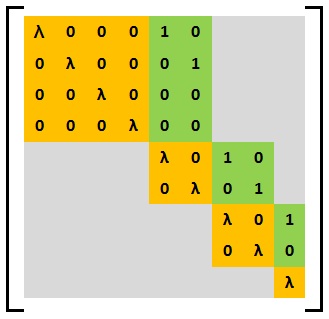
Пример элементарной матрицы Вейра:

$W=$$=\left[\begin{array}{cccc}{W}_{11}& W_{12}& & \\ & W_{22}& W_{23}& \\ & & W_{33}& W_{34}\\ & & & W_{44}\end{array}\right].$

В данной матрице $n=10$ и $n_1=4,n_2=2,n_3=2,n_4=1$. Таким образом, матрица $W$ имеет структуру Вейра $(4,2,2,1)$. Также

$W_{11}=\left[\begin{array}{cccc}\lambda & 0& 0& 0\\ 0& \lambda & 0& 0\\ 0& 0& \lambda & 0\\ 0& 0& 0& \lambda \end{array}\right]=\lambda I_4,W_{22}=\left[\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right]=\lambda I_2,W_{33}=\left[\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right]=\lambda I_2,W_{44}=\left[\begin{array}{c}\lambda \end{array}\right]=\lambda I_1$

и

$W_{12}=\left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& 0\\ 0& 0\end{array}\right],W_{23}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],W_{34}=\left[\begin{array}{c}1\\ 0\end{array}\right].$

Общая матрица Вейра

Пусть $W$ — квадратная матрица, а ${\lambda }_1,\dots ,{\lambda }_k$ — различные собственные значения матрицы $W$. Говорят, что $W$ — форма Вейра (или матрица Вейра), если $W$ имеет следующий вид:

$W=\left[\begin{array}{cccc}{W}_1& & & \\ & W_2& & \\ & & \ddots & \\ & & & W_k\end{array}\right],$

где $W_i$ — элементарная форма Вейра с собственным значением ${\lambda }_i$, где $i=1,\dots ,k$.

Применения формы Вейра

Некоторые известные применения формы Вейра:

1. Форма Вейра может быть использована для упрощения доказательства теоремы Герстенхабера, которая утверждает, что подалгебра, порождённая двумя коммутирующими $n\times n$-матрицами, имеет размерность не больше $n$.
2. Множество конечных матриц называется приближённо совместно диагонализуемым, если они могут быть возмущены до совместно диагонализуемых матриц. Форма Вейра используется для доказательства приближённой совместной диагонализации различных классов матриц. Свойство приближённой совместной диагонализуемости применяется при изучении филогенетических инвариантов в биоинформатике.
3. Форма Вейра может быть использована для упрощения доказательств неприводимости определённого ряда из всех возможных k-кортежей из коммутирующих матриц.