Гиперграф

Пример гиперграфа: $V=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7\}$, $E=\{e_1,e_2,e_3,e_4\}$ $=\{\{v_1,v_2,v_3\},\{v_2,v_3\},$ $\{v_3,v_5,v_6\},\{v_4\}\}$.

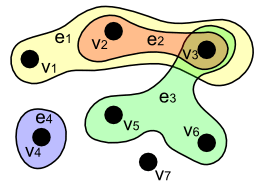
Гипергра́ф — обобщение графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества множества вершин.

С математической точки зрения, гиперграф представляет собой пару $(V,E)$, где $V$ — непустое множество объектов некоторой природы, называемых вершинами гиперграфа, а $E$ — семейство непустых (необязательно различных) подмножеств множества $V$, называемых рёбрами гиперграфа.

Гиперграфы применяются, в частности, при моделировании электрических цепей.

Трансверсалью гиперграфа является множество $T\subseteq V$, содержащее непустое пересечение с каждым ребром. Такая трансверсаль будет минимальной, если никакое её подмножество само не является трансверсалью гиперграфа.

Литература

• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Книга Шаблон:Wayback
• Шаблон:Статья