Топологическая сортировка

Топологическая сортировка — упорядочивание вершин ациклического ориентированного графа согласно частичному порядку, заданному рёбрами орграфа на множестве его вершин.

Например, для графа:

$G=\left(\right\{2,3,5,7,8,9,10,11\},\{(3,8),(3,10),(5,11),(7,11),(7,8),(8,9),(11,2),(11,9),(11,10)\left\}\right)$

существует несколько согласованных последовательностей его вершин, которые могут быть получены при помощи топологической сортировки, в частности:

• $7,5,11,3,8,2,9,10$
• $3,7,5,8,11,10,9,2$

В последовательности могут быть переставлены любые две стоящие рядом вершины, которые не входят в отношение частичного порядка $E$.

Ациклический ориентированный граф

Топологическая сортировка широко применяется в различных отраслях например, с её помощью можно построить последовательность прохождения учебных курсов студентами, последовательность установки программ при помощи пакетного менеджера, последовательность сборки исходных текстов программ по данным сборочных файлов, можно построить список отображения объектов в изометрической проекции зная парные порядковые отношения между объектами (какой из двух объектов должен быть прорисован раньше).

Алгоритм Кана

Один из первых алгоритмов, и наиболее приспособленный к исполнению вручную разработан Артуром Каном в 1962 году.

Пусть дан ациклический ориентированный простой граф $G=(V,E)$. Через $A(v),v\in V$ обозначим множество таких вершин $u\in V$, что $\mathrm{\exists }(u,v)\in E$. То есть $A(v)$ — множество всех вершин, из которых есть дуга в вершину $v$. Пусть $P$ — искомая последовательность вершин.

пока $|P|<|V|$
  выбрать любую вершину $v$ такую, что $A(v)=\varnothing$ и $v\notin P$
  $P\leftarrow P,v$
  удалить $v$ из всех $A(u),u\ne v$

Наличие хотя бы одного цикла в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину $v$.

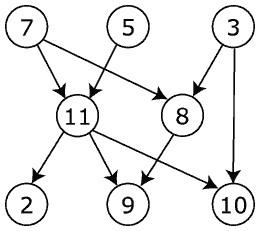
Например, если задан граф:

$G=\left(\right\{a,b,c,d,e\},\{(a,b),(a,c),(a,d),(a,e),(b,d),(c,d),(c,e),(d,e)\left\}\right)$,

алгоритм выполнится следующим образом:

шаг	$v$	$A(a)$	$A(b)$	$A(c)$	$A(d)$	$A(e)$	$P$
0	$-$	$\varnothing$	$a$	$a$	$a,b,c$	$a,c,d$	$\varnothing$
1	$a$	$\varnothing$	$\varnothing$	$\varnothing$	$b,c$	$c,d$	$a$
2	$c$	$\varnothing$	$\varnothing$	$\varnothing$	$b$	$d$	$a,c$
3	$b$	$\varnothing$	$\varnothing$	$\varnothing$	$\varnothing$	$d$	$a,c,b$
4	$d$	$\varnothing$	$\varnothing$	$\varnothing$	$\varnothing$	$\varnothing$	$a,c,b,d$
5	$e$	$\varnothing$	$\varnothing$	$\varnothing$	$\varnothing$	$\varnothing$	$a,c,b,d,e$

На втором шаге вместо $c$ может быть выбрана вершина $b$, поскольку порядок между $b$ и $c$ не задан.

Алгоритм Тарьяна

Шаблон:Main С использованием вычислительной техники топологическую сортировку можно выполнить за $O(n)$ времени и памяти, если обойти все вершины, используя поиск в глубину, и выводить вершины в момент выхода из неё — алгоритм разработан Робертом Тарьяном в 1976 году.

Изначально все вершины помечаются как белые, для каждой вершины осуществляется шаг алгоритма:

• если вершина чёрная, ничего делать не надо,
• если вершина серая — найден цикл, топологическая сортировка невозможна,
• если вершина белая, то:
  • красится в серый,
  • применяется шаг алгоритма для всех вершин, в которые можно попасть из текущей,
  • вершина красится в чёрный и помещается в начало окончательного списка.

Например, на графе:

$G=\left(\right\{a,b,c,d,e\},\{(a,b),(a,c),(a,d),(a,e),(b,d),(c,d),(c,e),(d,e)\left\}\right)$

с порядком обхода $c,d,e,a,b$ алгоритм отрабатывает следующим образом:

Шаг	Текущая	Белые	Стек (серые)	Выход (чёрные)
0	—	$a,b,c,d,e$	—	—
1	$c$	$a,b,d,e$	$c$	—
2	$d$	$a,b,e$	$c,d$	—
3	$e$	$a,b$	$c,d,e$	—
4	$d$	$a,b$	$c,d$	$e$
5	$c$	$a,b$	$c$	$d,e$
6	—	$a,b$	—	$c,d,e$
7	$d$	$a,b$	—	$c,d,e$
8	$e$	$a,b$	—	$c,d,e$
9	$a$	$b$	$a$	$c,d,e$
10	$b$	—	$a,b$	$c,d,e$
11	$a$	—	$a$	$b,c,d,e$
12	—	—	—	$a,b,c,d,e$
13	$b$	—	—	$a,b,c,d,e$

См. также

• Алгоритм Демукрона

Литература

• Шаблон:Source
• Шаблон:Книга:CLRS

Ссылки

• Топологическая сортировка при помощи поиска в глубину — реализация на C++
• Топологическая сортировка на Pascal за O(n + m) от Никлауса Вирта