Угловое ускорение

Угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени

$\overrightarrow{\epsilon }=\frac{d\overrightarrow{\omega }}{dt}.$

Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела.

Как приходят к понятию углового ускорения: ускорение точки твёрдого тела при свободном движении

К понятию углового ускорения можно прийти, рассматривая вычисление ускорения точки твёрдого тела, совершающего свободное движение. Скорость точки тела $B$ при свободном движении, согласно формуле Эйлера, равна

${\overrightarrow{v}}_B={\overrightarrow{v}}_A+\overrightarrow{\omega }\times \overrightarrow{AB},$

где ${\overrightarrow{v}}_A$ — скорость точки тела $A$, принятой в качестве полюса; $\overrightarrow{\omega }$ — псевдовектор угловой скорости тела; $\overrightarrow{AB}$ — вектор, выпущенный из полюса в точку, скорость которой вычисляется. Дифференцируя по времени данное выражение и используя формулу Ривальса, имеем

$\overrightarrow{a_B}=\overrightarrow{a_A}+\overrightarrow{\epsilon }\times \overrightarrow{AB}+\overrightarrow{\omega }\times (\overrightarrow{\omega }\times \overrightarrow{AB})$

$\overrightarrow{a_B}=\overrightarrow{a_A}+\overrightarrow{a_{BA}^{rot}}+\overrightarrow{a_{BA}^{axis}},$

где ${\overrightarrow{a}}_A$ — ускорение полюса $A$; $\overrightarrow{\epsilon }=\frac{d\overrightarrow{\omega }}{dt}$ — псевдовектор углового ускорения. Составляющая ускорения точки $B$, вычисляемая через угловое ускорение называется вращательным ускорением точки $B$ вокруг полюса $A$

${\overrightarrow{a}}_{BA}^{rot}=\overrightarrow{\epsilon }\times \overrightarrow{AB}.$

Последнее слагаемое в полученной формуле, зависящее от угловой скорости, называют осестремительным ускорением ускорением точки $B$ вокруг полюса $A$

${\overrightarrow{a}}_{BA}^{axis}=\overrightarrow{\omega }\times (\overrightarrow{\omega }\times \overrightarrow{AB}).$

Геометрический смысл псевдовектора углового ускорения

Псевдовектор $\overrightarrow{\epsilon }$ направлен по касательной к годографу угловой скорости. Действительно, рассмотрим два значения вектора угловой скорости, в момент времени $t$ и в момент времени $t+\mathrm{\Delta }t$. Оценим изменение угловой скорости за рассматриваемый промежуток времени $\mathrm{\Delta }t$

$\mathrm{\Delta }\overrightarrow{\omega }=\overrightarrow{\omega }(t+\mathrm{\Delta }t)-\overrightarrow{\omega }(t).$

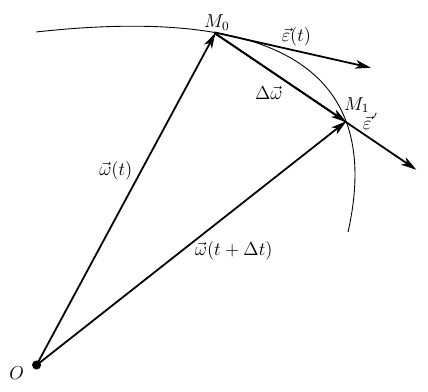
Отнесём это изменение к тому промежутку времени, за которое оно произошло

$\frac{\mathrm{\Delta }\overrightarrow{\omega }}{\mathrm{\Delta }t}={\overrightarrow{\epsilon }}^{{}^{\prime }}.$

Получившийся вектор называется вектором среднего углового ускорения. Он занимает положение секущей, пересекая годограф вектора угловой скорости в точках $M_0$ и $M_1$. Перейдём к пределу при $\mathrm{\Delta }t\to 0$

$\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }\overrightarrow{\omega }}{\mathrm{\Delta }t}=\frac{d\overrightarrow{\omega }}{dt}=\overrightarrow{\epsilon }.$

Вектор среднего углового ускорения перейдёт в вектор мгновенного углового ускорения и займёт положение касательной в точке $M_0$ к годографу угловой скорости.

Выражение вектора углового ускорения через параметры конечного поворота

При рассмотрении вращения тела через параметры конечного поворота, вектор углового ускорения можно расписать формулой

$\overrightarrow{\epsilon }=(1-\cos \phi )(\overrightarrow{u}\times \frac{d^2\overrightarrow{u}}{d{t}^2})+\dot{\phi }(1+\cos \phi )\frac{d\overrightarrow{u}}{dt}+\dot{\phi }\sin \phi (\overrightarrow{u}\times \frac{d\overrightarrow{u}}{dt})+\sin \phi \frac{d^2\overrightarrow{u}}{d{t}^2}+\ddot{\phi }\overrightarrow{u},$

где $\overrightarrow{u}$ — орт, задающий направление оси поворота; $\phi$ — угол, на который совершается поворот вокруг оси $\overrightarrow{u}$.

Угловое ускорение при вращении тела вокруг неподвижной оси

При вращении тела вокруг неподвижной оси, проходящей через неподвижные точки тела $O_1$ и $O_2$, производные орта оси вращения равны нулю

$\frac{d\overrightarrow{u}}{dt}=\frac{d^2\overrightarrow{u}}{d{t}^2}=0.$

В этом случае вектор углового ускорения определяется тривиально через вторую производную угла поворота

$\overrightarrow{\epsilon }=\ddot{\phi }\overrightarrow{u}$

или

$\overrightarrow{\epsilon }=\epsilon \overrightarrow{u},$

где $\epsilon =\ddot{\phi }$ — алгебраическая величина углового ускорения. В этом случае псевдовектор углового ускорения, как и угловая скорость, направлен вдоль оси вращения тела. Если первая и вторая производные угла поворота имеют одинаковый знак

($\dot{\phi }\ddot{\phi }>0$),

то вектор углового ускорения и вектор угловой скорости совпадают по направлению (тело вращается ускоренно). В противном случае, при $\dot{\phi }\ddot{\phi }<0$, векторы угловой скорости и углового ускорения направлены в противоположные стороны (тело вращается замедленно).

В курсе теоретической механики традиционным является подход, при котором понятие угловой скорости и углового ускорения вводится при рассмотрении вращения тела вокруг неподвижной оси. При этом в качестве закона движения рассматривается зависимость от времени угла поворота тела

$\phi =\phi (t).$

В этом случае закон движения точки тела может быть выражен естественным способом, как длина дуги окружности, пройденная точкой при повороте тела от некоторого начального положения ${\phi }_0=\phi (t_0).$

$s(t)=R(\phi (t)-{\phi }_0),$

где $R$ — расстояние от точки до оси вращения (радиус окружности, по которой движется точка). Дифференцируя последнее соотношение по времени получаем алгебраическую скорость точки

$\frac{ds}{dt}=v_{\tau }=R\frac{d\phi }{dt}=\omega R,$

где $\omega =\frac{d\phi }{dt}$ — алгебраическая величина угловой скорости. Ускорение точки тела при вращении может быть представлено как геометрическая сумма тангенциального и нормального ускорения

${\overrightarrow{a}}_M={\overrightarrow{a}}_M^{\tau }+{\overrightarrow{a}}_M^n,$

причём тангенциальное ускорение получается как производная от алгебраической скорости точки

$a_M^{\tau }=\frac{d{v}_{\tau }}{dt}=\frac{d}{dt}\left(\omega R\right)=R\frac{d\omega }{dt}=\epsilon R,$

где $\epsilon =\frac{d\omega }{dt}=\frac{d^2\phi }{d{t}^2}$ — алгебраическая величина углового ускорения. Нормальное ускорение точки тела может быть вычислено по формулам

$a_M^n=\frac{v_{\tau }^2}{R}={\omega }^{2}R.$

Выражение псевдовектора углового ускорения через тензор поворота тела

Если поворот твёрдого тела задан тензором ранга $(1,1)$ (линейным оператором), выраженным, например, через параметры конечного поворота

$B_m^p=(1-\cos \phi )u^p{u}_m+\cos \phi {\delta }_m^p+\sin \phi g^{pl}{ϵ}_{lkm}{u}^k,$

где ${\delta }_m^p$ — символ Кронекера; ${ϵ}_{lkj}$ — тензор Леви-Чивиты, то, псевдовектор углового ускорения может быть вычислен по формуле

${\epsilon }^i=\frac{1}{2}{ϵ}^{ikl}{g}_{lp}(B_m^{\text{'}p}{\ddot{B}}_k^m+{\dot{B}}_m^{\text{'}p}{\dot{B}}_k^m),$

где $B_m^{\text{'}p}$ — тензор обратного преобразования, равный

$B_m^{\text{'}p}=(1-\cos \phi )u^p{u}_m+\cos \phi {\delta }_m^p-\sin \phi g^{pl}{ϵ}_{lkm}{u}^k.$

Литература

1. Тарг С. М. Краткий курс теоретической механики — 10-е изд., перераб. и доп. — М.: Высш. шк., 1986 — 416 С.
2. Погорелов Д. Ю. Введение в моделирование динамики систем тел: Учебное пособие. — Брянск: БГТУ, 1997. — 197 С.