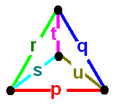
Тетраэдр Гурса

В евклидовом 3-пространстве существует 3 простых тетраэдра Гурса, которые представляются символами [4,3,4], [4,3^1,1] и [3^[4]]. Они могут рассматриваться как точки на кубе и внутри куба {4,3}.

Тетраэдр Гурса — тетраэдральная фундаментальная область построения Витхоффа. Каждая грань тетраэдра представляет зеркальную гиперплоскость на 3-мерной поверхности — 3-сферы, евклидового 3-мерного пространства и гиперболического 3-мерного пространства. Коксетер назвал область именем Эдуара Гурса, который первым обратил внимание на эти области. Тетраэдр Гурса является расширением теории треугольников Шварца для построения Витхоффа на сфере.

Графическое представление

Тетраэдр Гурса может быть представлен графически тетраэдральным графом, который является двойственной конфигурацией фундаментальной области в виде тетраэдра. В этом графе каждый узел представляет грань (зеркало) тетраэдра Гурса. Каждое ребро помечено рациональным числом, соответствующим порядку отражения, который равен $\pi$/двугранный угол.

4-вершинная диаграмма Коксетера — Дынкина представляет эти тетраэдральные графы со скрытыми рёбрами второго порядка. Если много рёбер имеют порядок 2, группа Коксетера может быть представлена Шаблон:Не переведено 5.

Для существования тетраэдра Гурса каждый из подграфов с 3 вершинами этого графа, (p q r), (p u s), (q t u) и (r s t), должны соответствовать треугольнику Шварца.

Внешняя симметрия

Симметрия тетраэдра Гурса может быть тетраэдральной симметрией любой подгруппы симметрии, показанной в дереве цветом рёбер.

Шаблон:Clear Расширенная симметрия тетраэдра Гурса является полупрямым произведением группы Коксетера симметрии и фундаментальной области симметрии (тетраэдра Гурса, в этом случае). Шаблон:Не переведено 5 поддерживает эту симметрию как вложенные скобки, наподобие [Y[X]], что означает полную группу Коксетера симметрии [X] с Y в качестве симметрии тетраэдра Гурса. Если Y является чистой зеркальной симметрией, группа будет представлять другую группу Коксетера отражений. Если имеется только одна простая удваивающая симметрия, Y может быть выражена явно, наподобие [[X]] с зеркальной или вращательной симметрией, в зависимости от контекста.

Расширенная симметрия каждого тетраэдра Гурса задана ниже. Наивысшая возможная симметрия у правильного тетраэдра, [3,3], и она достигается на призматической точечной группе [2,2,2], или [2^[3,3]], и на паракомпактной гиперболической группе [3^[3,3]].

См. симметрии тетраэдра для 7 симметрий низкого порядка тетраэдра.

Полное число решений

Последующие секции показывают все из полного набора решений тетраэдров Гурса для 3-сферы, евклидова 3-мерного пространства и гиперболического 3-мерного пространства. Расширенная симметрия каждого тетраэдра тоже указана.

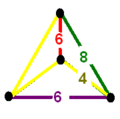
Цветные тетраэдральные диаграммы ниже являются вершинными фигурами Шаблон:Не переведено 5 многогранников и сот из каждого семейства симметрий. Метки рёбер представляют порядки многоугольных граней, которые являются удвоенными порядками ветвей графа Коксетера. Двугранный угол ребра, помеченного 2n, равен $\pi /n$. Жёлтые рёбра, помеченные цифрой 4, получаются из прямого угла (несвязанных) зеркал (узлов) диаграммы Коксетера.

(Конечные) решения на 3-сфере

Изоморфизм конечных групп Коксетера

Решения для 3-сферы с плотностью 1: (однородные многогранники)

Дуопризмы и гиперпризмы:

Группа Коксетера и диаграмма	[2,2,2] Шаблон:CDD	[p,2,2] Шаблон:CDD	[p,2,q] Шаблон:CDD	[p,2,p] Шаблон:CDD	[3,3,2] Шаблон:CDD	[4,3,2] Шаблон:CDD	[5,3,2] Шаблон:CDD
Порядок группы симметрии	16	8p	4pq	4p2	48	96	240
Симметрии тетраэдра	[3,3] (порядок 24)	[2] (порядок 4)	[2] (порядок 4)	[2+,4] (порядок 8)	[ ] (порядок 2)	[ ]+ (порядок 1)	[ ]+ (порядок 1)
Расширенные симметрии	[(3,3)[2,2,2]] Шаблон:CDD =[4,3,3] Шаблон:CDD	[2[p,2,2]] Шаблон:CDD =[2p,2,4] Шаблон:CDD	[2[p,2,q]] Шаблон:CDD =[2p,2,2q] Шаблон:CDD	[(2+,4)[p,2,p]] Шаблон:CDD =[2+[2p,2,2p]] Шаблон:CDD	[1[3,3,2]] Шаблон:CDD =[4,3,2] Шаблон:CDD	[4,3,2] Шаблон:CDD	[5,3,2] Шаблон:CDD
Порядок расширенных групп симметрии	384	32p	16pq	32p2	96	96	240

Тип графа	Линейный				Трёхлистный
Группа Коксетера и диаграмма	Пяти- ячейный Шаблон:Не переведено 5 Шаблон:CDD	Шестнадцати- ячейный Шаблон:Не переведено 5 Шаблон:CDD	Двадцати- четырёхъ- ячейный Шаблон:Не переведено 5]] Шаблон:CDD	Шестисот- ячейный Шаблон:Не переведено 5 Шаблон:Не переведено 5 Шаблон:CDD	Полутессеракт Шаблон:Не переведено 5 Шаблон:CDD
Вершинная фигура всеусечённых однородных многогранников
Тетраэдр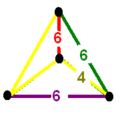
Порядок группы симметрии	120	384	1152	14400	192
Тетраэдральная симметрия	[2]+ (порядок 2)	[ ]+ (порядок 1)	[2]+ (порядок 2)	[ ]+ (порядок 1)	[3] (порядок 6)
Расширенная симметрия	[2+[3,3,3]] Шаблон:CDD	[4,3,3] Шаблон:CDD	[2+[3,4,3]] Шаблон:CDD	[5,3,3] Шаблон:CDD	[3[31,1,1]] Шаблон:CDD =[3,4,3] Шаблон:CDD
Порядок группы расширенной симметрии	240	384	2304	14400	1152

Решения в евклидовом 3-мерном пространстве

Изоморфизмы евклидовых групп Коксетера

Решения плотности 1: Шаблон:Не переведено 5:

Тип графа	Линейный	Трёхлистный	Кольцо	Призматический			Вырожденный
Группа Коксетера Диаграмма Коксетера	Шаблон:Не переведено 5 Шаблон:CDD	Шаблон:Не переведено 5 Шаблон:CDD	Шаблон:Не переведено 5 Шаблон:CDD	[4,4,2] Шаблон:CDD	[6,3,2] Шаблон:CDD	[3[3],2] Шаблон:CDD	[∞,2,∞] Шаблон:CDD
Вершинная фигура всеусечённых сот
Тетраэдр
Тетраэдральная симметрия	[2]+ (порядок 2)	[ ] (порядок 2)	[2+,4] (порядок 8)	[ ] (порядок 2)	[ ]+ (порядок 1)	[3] (порядок 6)	[2+,4] (порядок 8)
Расширенная симметрия	[(2+)[4,3,4]] Шаблон:CDD	[1[4,31,1]] Шаблон:CDD =[4,3,4] Шаблон:CDD	[(2+,4)[3[4]]] Шаблон:CDD =[2+[4,3,4]] Шаблон:CDD	[1[4,4,2]] Шаблон:CDD =[4,4,2] Шаблон:CDD	[6,3,2] Шаблон:CDD	[3[3[3],2]] Шаблон:CDD =[3,6,2] Шаблон:CDD	[(2+,4)[∞,2,∞]] Шаблон:CDD =[1[4,4]] Шаблон:CDD

Решения для гиперболических 3-пространств

Решения плотности 1: (Шаблон:Не переведено 5) (Компакт (группы симплексов Ланнера))

Группы симплексов Ланнера ранга 4

Тип графа	Линейный			Трёхлистный
Группа Коксетера Диаграмма Коксетера	[3,5,3] Шаблон:CDD	[5,3,4] Шаблон:CDD	[5,3,5] Шаблон:CDD	[5,31,1] Шаблон:CDD
Вершинный фигуры всеусечённых сот
Тетраэдр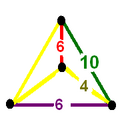
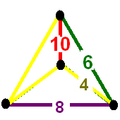
Тетраэдральная симметрия	[2]+ (порядок 2)	[ ]+ (порядок 1)	[2]+ (порядок 2)	[ ] (порядок 2)
Расширенная симметрия	[2+[3,5,3]] Шаблон:CDD	[5,3,4] Шаблон:CDD	[2+[5,3,5]] Шаблон:CDD	[1[5,31,1]] Шаблон:CDD =[5,3,4] Шаблон:CDD
Тип графа	Кольцо
Группа Коксетера Диаграмма Коксетера	[(4,3,3,3)] Шаблон:CDD	[(4,3)2] Шаблон:CDD	[(5,3,3,3)] Шаблон:CDD	[(5,3,4,3)] Шаблон:CDD	[(5,3)2] Шаблон:CDD
Вершинные фигуры всеусечённых сот
Тетраэдр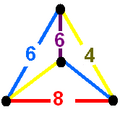
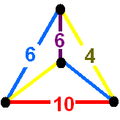
Тетраэдральная симметрия	[2]+ (порядок 2)	[2,2]+ (порядок 4)	[2]+ (порядок 2)	[2]+ (порядок 2)	[2,2]+ (порядок 4)
Расширенная симметрия	[2+[(4,3,3,3)]] Шаблон:CDD	[(2,2)+[(4,3)2]] Шаблон:CDD	[2+[(5,3,3,3)]] Шаблон:CDD	[2+[(5,3,4,3)]] Шаблон:CDD	[(2,2)+[(5,3)2]] Шаблон:CDD

Решения в паракомпактных гиперболических 3-пространствах

Здесь показана связь подгрупп паракомпактного гиперболического тетраэдра Гурса. Подгруппы порядка 2 представляют разбиение тетраэдра Гурса плоскостью зеркальной симметрии

Решения плотности 1: (См. Паракомпакт (группы симплексов Козула))

Группы симплексов Козула ранга 4

Тип графа	Линейные графы
Группа Коксетера Диаграмма Коксетера	[6,3,3] Шаблон:CDD	[3,6,3] Шаблон:CDD	[6,3,4] Шаблон:CDD	[6,3,5] Шаблон:CDD	[6,3,6] Шаблон:CDD	[4,4,3] Шаблон:CDD	[4,4,4] Шаблон:CDD
Тетраэдральная симметрия	[ ]+ (порядок 1)	[2]+ (порядок 2)	[ ]+ (порядок 1)	[ ]+ (порядок 1)	[2]+ (порядок 2)	[ ]+ (порядок 1)	[2]+ (порядок 2)
Расширенная симметрия	[6,3,3] Шаблон:CDD	[2+[3,6,3]] Шаблон:CDD	[6,3,4] Шаблон:CDD	[6,3,5] Шаблон:CDD	[2+[6,3,6]] Шаблон:CDD	[4,4,3] Шаблон:CDD	[2+[4,4,4]] Шаблон:CDD
Тип графа	Кольцевые графы
Группа Коксетера Диаграмма Коксетера	[3[ ]×[ ]] Шаблон:CDD	[(4,4,3,3)] Шаблон:CDD	[(43,3)] Шаблон:CDD	[4[4]] Шаблон:CDD	[(6,33)] Шаблон:CDD	[(6,3,4,3)] Шаблон:CDD	[(6,3,5,3)] Шаблон:CDD	[(6,3)[2]] Шаблон:CDD
Тетраэдральная симметрия	[2] (порядок 4)	[ ] (порядок 2)	[2]+ (порядок 2)	[2+,4] (порядок 8)	[2]+ (порядок 2)	[2]+ (порядок 2)	[2]+ (порядок 2)	[2,2]+ (порядок 4)
Расширенная симметрия	[2[3[ ]×[ ]]] Шаблон:CDD =[6,3,4] Шаблон:CDD	[1[(4,4,3,3)]] Шаблон:CDD =[3,41,1] Шаблон:CDD	[2+[(43,3)]] Шаблон:CDD	[(2+,4)[4[4]]] Шаблон:CDD =[2+[4,4,4]] Шаблон:CDD	[2+[(6,33)]] Шаблон:CDD	[2+[(6,3,4,3)]] Шаблон:CDD	[2+[(6,3,5,3)]] Шаблон:CDD	[(2,2)+[(6,3)[2]]] Шаблон:CDD
Тип графа	Трёхлистный			Кольцо с хвостом				Симлекс
Группа Коксетера Диаграмма Коксетера	[6,31,1] Шаблон:CDD	[3,41,1] Шаблон:CDD	[41,1,1] Шаблон:CDD	[3,3[3]] Шаблон:CDD	[4,3[3]] Шаблон:CDD	[5,3[3]] Шаблон:CDD	[6,3[3]] Шаблон:CDD	[3[3,3]] Шаблон:CDD
Тетраэдральная симметрия	[ ] (порядок 2)	[ ] (порядок 2)	[3] (порядок 6)	[ ] (порядок 2)	[ ] (порядок 2)	[ ] (порядок 2)	[ ] (порядок 2)	[3,3] (порядок 24)
Расширенная симметрия	[1[6,31,1]] Шаблон:CDD =[6,3,4] Шаблон:CDD	[1[3,41,1]] Шаблон:CDD =[3,4,4] Шаблон:CDD	[3[41,1,1]] Шаблон:CDD =[4,4,3] Шаблон:CDD	[1[3,3[3]]] Шаблон:CDD =[3,3,6] Шаблон:CDD	[1[4,3[3]]] Шаблон:CDD =[4,3,6] Шаблон:CDD	[1[5,3[3]]] Шаблон:CDD =[5,3,6] Шаблон:CDD	[1[6,3[3]]] Шаблон:CDD =[6,3,6] Шаблон:CDD	[(3,3)[3[3,3]]] Шаблон:CDD =[6,3,3] Шаблон:CDD

Рациональные решения

Существует сотни рациональных решений для 3-сфер, включая эти 6 линейных графов, которые образуют многогранники Шлефли–Гесса, и 11 нелинейных:

Линейные графы Плотность 4: [3,5,5/2] Шаблон:CDD Плотность 6: [5,5/2,5] Шаблон:CDD Плотность 20: [5,3,5/2] Шаблон:CDD Плотность 66: [5/2,5,5/2] Шаблон:CDD Плотность 76: [5,5/2,3] Шаблон:CDD Плотность 191: [3,3,5/2] Шаблон:CDD

Графы «кольцо с хвостом»: Плотность 2: Шаблон:CDD Плотность 3: Шаблон:CDD Плотность 5: Шаблон:CDD Плотность 8: Шаблон:CDD Плотность 9: Шаблон:CDD Плотность 14: Шаблон:CDD Плотность 26: Шаблон:CDD Плотность 30: Шаблон:CDD Плотность 39: Шаблон:CDD Плотность 46: Шаблон:CDD Плотность 115: Шаблон:CDD

См. также

• Точечная группа симметрии для n-симплексных решений на (n-1)-сфере.

Литература

• Шаблон:Книга

• Шаблон:Книга Джонсон доказал, что перечисление тетраэдров Гурса Коксетером полно.
• Шаблон:Статья
• Klitzing, Richard.Dynkin Diagrams Goursat tetrahedra
• Шаблон:Книга
• Шаблон:Книга