Сеть Фейстеля

Сеть Фе́йстеля, или конструкция Фейстеля (Шаблон:Lang-en), — один из методов построения блочных шифров. Сеть состоит из ячеек, называемых ячейками Фейстеля. На вход каждой ячейки поступают данные и ключ. На выходе каждой ячейки получают изменённые данные и изменённый ключ. Все ячейки однотипны, и говорят, что сеть представляет собой определённую многократно повторяющуюся (итерированную) структуру. Ключ выбирается в зависимости от алгоритма шифрования/расшифрования и меняется при переходе от одной ячейки к другой. При шифровании и расшифровании выполняются одни и те же операции; отличается только порядок ключей. Ввиду простоты операций сеть Фейстеля легко реализовать как программно, так и аппаратно. Ряд блочных шифров (DES, RC2, RC5, RC6, Blowfish, FEAL, CAST-128, TEA, XTEA, XXTEA и др.) использует сеть Фейстеля в качестве основы. Альтернативой сети Фейстеля является подстановочно-перестановочная сеть (AES и др.).

История

В 1971 году Хорст Фейстель запатентовал два устройства, реализующих различные алгоритмы шифрования, позже получившие название «Люцифер» (Шаблон:Lang-en). Одно из этих устройств использовало конструкцию, впоследствии названную «сетью Фейстеля» (Шаблон:Lang-en, Шаблон:Lang-en2). Тогда Фейстель работал над созданием новых криптосистем в стенах IBM вместе с Доном Копперсмитом. Проект «Люцифер» был скорее экспериментальным, но стал основой для алгоритма DES (Шаблон:Lang-en). В 1973 году журнал «Scientific American» опубликовал статью Фейстеля «Криптография и компьютерная безопасность» (Шаблон:Lang-en), в которой раскрыты некоторые важные аспекты шифрования и приведено описание первой версии проекта «Люцифер». В первой версии проекта «Люцифер» сеть Фейстеля не использовалась.

На основе сети Фейстеля был спроектирован алгоритм DES. В 1977 году власти США приняли стандарт Шаблон:Nobr, признающий DES стандартным методом шифрования данных. DES некоторое время широко использовался в криптографических системах. Итеративная структура алгоритма позволяла создавать простые программные и аппаратные реализации.

Согласно некоторым данным, в СССР уже в 1970-е годы КГБ разрабатывала блочный шифр, использовавший сеть Фейстеля, и, вероятно, именно этот шифр в 1990 году был принят в качестве ГОСТ 28147-89.

В 1987 году были разработаны алгоритмы FEAL и RC2. Сети Фейстеля получили широкое распространение в 1990-е годы — в годы появления таких алгоритмов, как Blowfish (1993), TEA (1994), RC5 (1994), CAST-128 (1996), XTEA (1997), XXTEA (1998), RC6 (1998) и других.

2 января 1997 года институт NIST объявил конкурс по созданию нового алгоритма шифрования данных, призванного заменить DES. Новый блочный шифр получил название AES (Шаблон:Lang-en) и был утверждён 26 мая 2002 года. В AES вместо сети Фейстеля используется подстановочно-перестановочная сеть.

Конструкция блочного шифра на основе сетей Фейстеля

Простое описание

Шифрование

Пусть требуется зашифровать некоторую информацию, представленную в двоичном виде (в виде последовательности нулей и единиц) и находящуюся в памяти компьютера или иного устройства (например, в файле).

Алгоритм шифрования.

• Информация разбивается на блоки одинаковой (фиксированной) длины. Полученные блоки называются входными, так как поступают на вход алгоритма. В случае, если длина входного блока меньше, чем размер, который выбранный алгоритм шифрования способен зашифровать единовременно (размер блока), блок удлиняется каким-либо способом. Как правило, длина блока является степенью двойки, например, составляет 64 бита или 128 бит.

Далее будем рассматривать операции, происходящие только с одним блоком, так как в процессе шифрования с другими блоками выполняются те же самые операции.

• Выбранный блок делится на два подблока одинакового размера — «левый» ($L_0$) и «правый» ($R_0$).
• «Правый подблок» $R_0$ изменяется функцией F с использованием раундового ключа $K_0$:

$x=F(R_0,K_0).$

• Результат складывается по модулю 2 («xor») с «левым подблоком» $L_0$:

$x=x\oplus L_0.$

• Результат будет использован в следующем раунде в роли «правого подблока» $R_1$:

$R_1=x.$

• «Правый подблок» $R_0$ текущего раунда (в своем не измененном на момент начала раунда виде) будет использован в следующем раунде в роли «левого подблока» $L_1$:

$L_1=R_0.$

• По какому-либо математическому правилу вычисляется раундовый ключ $K_1$ — ключ, который будет использоваться в следующем раунде.

Перечисленные операции выполняются N-1 раз, где N — количество раундов в выбранном алгоритме шифрования. При этом между переходами от одного раунда (этапа) к другому изменяются ключи: $K_0$ заменяется на $K_1$, $K_1$ — на $K_2$ и т. д.).

Расшифрование

Расшифровка информации происходит так же, как и шифрование, с тем лишь исключением, что ключи следуют в обратном порядке, то есть не от первого к N-му, а от N-го к первому.

Алгоритмическое описание

• Блок открытого текста делится на две равные части: $(L_0,R_0)$.
• В каждом раунде вычисляются:

$L_i=R_{i-1}\oplus f(L_{i-1},K_{i-1});$

$R_i=L_{i-1},$

где:

• i — номер раунда; $i=1\dots N;$
• N — количество раундов в выбранном алгоритме шифрования;
• $f$ — некоторая функция;
• $K_{i-1}$ — ключ i-1-го раунда (раундовый ключ).

Результатом выполнения $N$ раундов является $(L_N,R_N)$. В N-м раунде перестановка $L_N$ и $R_N$ не производится, чтобы была возможность использовать ту же процедуру и для расшифрования, просто инвертировав порядок использования ключей ($K_N,K_{N-1},\dots ,K_0$ вместо $K_0,K_1,\dots ,K_N$):

$L_{i-1}=R_i\oplus f(L_i,K_{i-1})$

$R_{i-1}=L_i.$

Небольшим изменением можно добиться и полной идентичности процедур шифрования и расшифрования.

Достоинства:

• обратимость алгоритма независимо от используемой функции f;
• возможность выбора сколь угодно сложной функции f.

Математическое описание

Рассмотрим пример. Пусть:

• X — блок данных, поступающий на вход (входной блок);
• A — некоторое инволютивное преобразование (или инволюция) — взаимно-однозначное преобразование, которое является обратным самому себе, то есть [[Квантор всеобщности|для каждого Шаблон:Symbol]] X справедливо выражение:

$AAX=A^{2}X=X,\mathrm{\forall }X;$

• Y — блок данных, получаемый на выходе (результат).

При однократном применении преобразования A к входному блоку X получится выходной блок Y:

$Y=AX.$

При применении преобразования A к результату предыдущего преобразования — Y получится:

$AY=AAX=X,\mathrm{\forall }X.$

Пусть входной блок X состоит из двух подблоков L и R равной длины:

$X=(L,R).$

Определим два преобразования:

• $G(X,K)$ — шифрование данных X с ключом K:

$G(X,K)=G((L,R),K)=(L\oplus F(K,R),R);$

• $T(L,R)$ — перестановка подблоков L и R:

$T(L,R)=(R,L).$

Введём обозначения:

• однократное применение преобразования G:

$\tilde{X}=(\tilde{L},\tilde{R})=GX;$

• двукратное применение преобразования G:

$\widetilde{\stackrel{~}{X}}=(\widetilde{\stackrel{~}{L}},\widetilde{\stackrel{~}{R}})=G^{2}X.$

Докажем инволютивность двукратного преобразования G ($G^2$).

Несложно заметить, что преобразование G меняет только левый подблок L, оставляя правый R неизменным:

$\tilde{L}=L\oplus F(K,R);$

$\tilde{R}=R.$

Поэтому далее будем рассматривать только подблок L. После двукратного применения преобразования G к L получим:

$\widetilde{\stackrel{~}{L}}=\tilde{L}\oplus F(K,\tilde{R})=\tilde{L}\oplus F(K,R)=L\oplus F(K,R)\oplus F(K,R)=L.$

Таким образом:

$G^{2}L=L;$

$G^{2}R=R,$

следовательно

$G^{2}X=X$

и G — инволюция.

Докажем инволютивность двукратного преобразования T ($T^2$).

$T^{2}X=T^2(L,R)=T(R,L)=(L,R)=X.$

Рассмотрим процесс шифрования. Пусть:

• X — входное значение;
• $G_i$ — преобразование с ключом $K_i$;
• $Y_i$ — выходное значение, результат i-го раунда.

Тогда преобразование, выполняемое на i+1-м раунде, можно записать в виде:

$Y_{i+1}=T{G}_i{Y}_i$.

Преобразование, выполняемое на 1-м раунде:

$Y_1=T{G}_{1}X.$

Следовательно, выходное значение после m раундов шифрования будет равно:

$Y_m=T{G}_m{Y}_{m-1}=T{G}_{m}T{G}_{m-1}\dots T{G}_{1}X.$

Можно заметить, что на последнем этапе не обязательно выполнять перестановку T.

Расшифрование ведётся применением всех преобразований в обратном порядке. В силу инволютивности каждого из преобразований обратный порядок даёт исходный результат:

$X=G_{1}T{G}_{2}T\dots G_{m-1}T{G}_{m}T(Y_m)=G_{1}T{G}_{2}T\dots G_{m-1}T(Y_{m-1})=\dots =G_{1}T(Y_1)=X.$

Функции, используемые в сетях Фейстеля

В своей работе «Криптография и компьютерная безопасность» Хорст Фейстель описывает два блока преобразований (функций $f(L_i,K_i)$):

• блок подстановок (s-блок, Шаблон:Lang-en);
• блок перестановок (p-блок, Шаблон:Lang-en).

Можно показать, что любое двоичное преобразование над блоком данных фиксированной длины может быть реализовано в виде s-блока. В силу сложности строения N-разрядного s-блока при больших N на практике применяют более простые конструкции.

Термин «блок» в оригинальной статье используется вместо термина «функция» вследствие того, что речь идёт о блочном шифре и предполагалось, что s- и p-блоки будут цифровыми микросхемами (цифровыми блоками).

Файл:S-block.svg

Принципиальная схема 3-разрядного s-блока

Файл:Feistel Network P-Block.png

Принципиальная схема 8-разрядного p-блока

S-блок

Шаблон:Main Блок подстановок (s-блок, Шаблон:Lang-en) состоит из следующих частей:

• дешифратор — преобразователь n-разрядного двоичного сигнала в одноразрядный сигнал по основанию $2^n$;
• система коммутаторов — внутренние соединения (всего возможных соединений $2^n!$);
• шифратор — преобразователь сигнала из одноразрядного $2^n$-ричного в n-разрядный двоичный.

Анализ n-разрядного S-блока при большом n крайне сложен, однако реализовать такой блок на практике очень сложно, так как число возможных соединений крайне велико ($2^n$). На практике блок подстановок используется как часть более сложных систем.

В общем случае s-блок может иметь несовпадающее число входов/выходов, в этом случае в системе коммутации от каждого выхода дешифратора может идти не строго одно соединение, а 2 или более или не идти вовсе. То же самое справедливо и для входов шифратора.

В электронике можно непосредственно применять приведённую справа схему. В программировании же генерируют таблицы замены. Оба этих подхода являются эквивалентными, то есть файл, зашифрованный на компьютере, можно расшифровать на электронном устройстве и наоборот.

Таблица замены для приведённого 3-разрядного s-блока

№ комбинации	0	1	2	3	4	5	6	7
Вход	000	001	010	011	100	101	110	111
Выход	011	000	001	100	110	111	010	101

P-блок

Блок перестановок (p-блок, Шаблон:Lang-en) всего лишь изменяет положение цифр и является линейным устройством. Этот блок может иметь очень большое количество входов-выходов, однако в силу линейности систему нельзя считать криптоустойчивой.

Криптоанализ ключа для n-разрядного p-блока проводится путём подачи на вход n-1 различных сообщений, каждое из которых состоит из n-1 нуля («0») и 1 единицы («1») (или наоборот, из единиц и нуля).

Циклический сдвиг

Циклический сдвиг влево на 3 разряда 8-битной шины

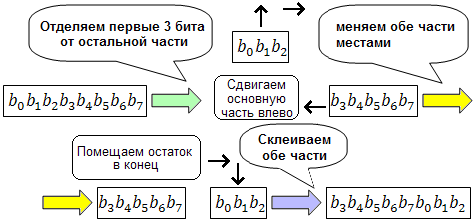
Можно показать, что циклический сдвиг является частным случаем p-блока.

В простейшем случае (сдвиг на 1 бит), крайний бит отщепляется и перемещается на другой конец регистра или шины. В зависимости от того какой бит берётся, правый или левый, сдвиг называется вправо или влево. Сдвиги на большее число бит можно рассматривать, как многократное применение сдвига на 1.

Циклический сдвиг на m бит для n-разрядного входа (m < n)

Направление сдвига	Порядок следования битов до сдвига	Порядок следования битов после сдвига
Влево	$b_0,b_1,b_2,...,b_{n-1}$	$b_m,b_{m+1},...b_{n-1},b_0,b_1,...,b_{m-1}$
Вправо	$b_0,b_1,b_2,...,b_{n-1}$	$b_{n-m},b_{n-m+1},...b_{n-1},b_0,b_1,...,b_{n-m-1}$

Сложение по модулю n

Операция «сложение по модулю n» обозначается как

(A + B) mod n

и представляет собой остаток от деления суммы Шаблон:Nobr на n, где A и B — числа.

Можно показать, что сложение двух чисел по модулю n представляется в двоичной системе счисления в виде s-блока, у которого на вход подаётся число A, а в качестве системы коммутации s-блока используется циклический сдвиг влево на B разрядов.

В компьютерной технике и электронике операция сложения, как правило, реализована как сложение по модулю $n=2^m$, где m — целое (обычно m равно разрядности машины). Для получения в двоичной системе

A + B mod $2^m$

достаточно сложить числа, после чего отбросить разряды начиная с m-го и старше.

Умножение по модулю n

Умножение по модулю n обозначается как

(A * B) mod n

и представляет собой остаток от деления произведения Шаблон:Nobr на n, где A и B — числа.

В персональных компьютерах на платформе x86 при перемножении двух m-разрядных чисел получается число разрядностью 2*m. Чтобы получить остаток от деления на $2^m$, нужно отбросить m старших бит.

Пример реализации на языке Си

Общий вид алгоритма шифрования, использующего сеть Фейстеля:

/* Функция, выполняющая преобразование подблока с учётом значения ключа (по ключу). 
Реализация зависит от выбранного алгоритма блочного шифрования. */
int f (
        int subblock,  /* преобразуемый подблок */
        int key        /* ключ */
);  /* возвращаемое значение - преобразованный блок */

/* Функция, выполняющая шифрование открытого текста */
void crypt (
        int * left,   /* левый входной подблок */
        int * right,  /* правый входной подблок */
        int rounds,   /* количество раундов */
        int * key     /* массив ключей (по ключу на раунд) */
) {
    int i, temp;
    for ( i = 0; i < rounds; i++ )
    {
        temp = *right ^ f( *left, key[i] );
        *right = *left;
        *left = temp;
    }
}

/* Функция, выполняющая расшифрование текста */
void decrypt (
        int * left,   /* левый зашифрованный подблок */
        int * right,  /* правый зашифрованный подблок */
        int rounds,   /* количество раундов */
        int * key     /* массив ключей (по ключу на раунд) */
) {
    int i, temp;
    for ( i = rounds - 1; i >= 0; i-- )
    {
        temp = *left ^ f( *right, key[i] );
        *left = *right;
        *right = temp;
    }
}

Достоинства и недостатки

Достоинства:

• простота аппаратной реализации на современной электронной базе;
• простота программной реализации в силу того, что значительная часть функций поддерживается на аппаратном уровне в современных компьютерах (например, сложение по модулю 2 («xor»), сложение по модулю $2^n$, умножение по модулю $2^n$, и т. д.);
• хорошая изученность алгоритмов, построенных на основе сетей Фейстеля.

Недостатки:

• за один раунд шифруется только половина входного блокаШаблон:Sfn.

Теоретические исследования

Сети Фейстеля были широко изучены криптографами в силу их обширного распространения. В 1988 году Шаблон:Iw и Шаблон:Iw провели исследования сети Фейстеля и доказали, что если раундовая функция является криптостойкой псевдослучайной, а используемые ключи независимы в каждом раунде, то 3 раундов будет достаточно для того, чтобы блочный шифр являлся псевдослучайной перестановкой, тогда как четырёх раундов будет достаточно для того, чтобы сделать сильную псевдослучайную перестановку.

«Псевдослучайной перестановкой» Люби и Ракофф назвали такую, которая устойчива к атаке с адаптивным выбором открытого текста, а «сильной псевдослучайной перестановкой» — псевдослучайную перестановку, устойчивую к атаке с использованием выбранного шифрованного текста.

Иногда в западной литературе сеть Фейстеля называют «Luby-Rackoff block cipher» в честь Люби и Ракоффа, которые проделали большой объём теоретических исследований в этой области.

В дальнейшем, в 1997 году Шаблон:Iw и Шаблон:Iw предложили упрощённый вариант конструкции Люби — Ракоффа, состоящий из четырёх раундов. В этом варианте в качестве первого и последнего раунда используются две попарно-независимые перестановки. Два средних раунда конструкции Наора — Рейнголда идентичны раундам в конструкции Люби — Ракоффа.

Большинство же исследований посвящено изучению конкретных алгоритмов. Во многих блочных шифрах на основе сети Фейстеля были найдены те или иные уязвимости, однако в ряде случаев эти уязвимости являются чисто теоретическими и при нынешней производительности компьютеров использовать их на практике для взлома невозможно.

Модификации сети Фейстеля

При большом размере блоков шифрования (128 бит и более) реализация такой конструкции Фейстеля на 32-разрядных архитектурах может вызвать затруднения, поэтому применяются модифицированные варианты этой конструкции. Обычно используются сети с четырьмя ветвями. На рисунке показаны наиболее распространённые модификации. Также существуют схемы, в которых длины половинок $L_0$ и $R_0$ не совпадают. Такие сети называются несбалансированными.

• Модификации сети Фейстеля
• 
  Тип 1
• 
  Тип 2
• 
  Тип 3

Алгоритм IDEA

Источник Шаблон:Sfn:

Схема одной итерации полного раунда алгоритма IDEA

В алгоритме IDEA используется глубоко модифицированная сеть Фейстеля. В нём 64-битные входные блоки данных (обозначим за $X_0$) делятся на 4 подблока длиной 16 бит $X_0=\{X^{(0)}{X}^{(1)}{X}^{(2)}{X}^{(3)}\}$. На каждом этапе используется 6 16-битных ключей. Всего используется 8 основных этапов и 1 укороченный.

Формулы для вычисления значения подблоков на i-м раунде (для раундов c 1-го по 8-й):

• предварительные вычисления:

$A_i=((X_{i-1}^{(0)}*K_i^{(1)})\oplus (X_{i-1}^{(2)}+K_i^{(3)}))*K_i^{(5)};$

$B_i=(((X_{i-1}^{(1)}+K_i^{(2)})\oplus (X_{i-1}^{(3)}*K_i^{(4)})+A_i)*K_i^{(6)});$

$C_i=((X_{i-1}^{(1)}+K_i^{(2)})\oplus (X_{i-1}^{(3)}*K_i^{(4)})+((X_{i-1}^{(0)}*K_i^{(1)})\oplus (X_{i-1}^{(2)}+K_i^{(3)}))*K_i^{(5)})*K_i^{(6)};$

• финальные вычисления:

$X_i^{(0)}=(X_{i-1}^{(0)}*K_i^{(1)})\oplus B_i;$

$X_i^{(1)}=(X_{i-1}^{(2)}+K_i^{(3)})\oplus B_i;$

$X_i^{(2)}=(X_{i-1}^{(1)}+K_i^{(2)})\oplus (A_i+C_i);$

$X_i^{(3)}=(X_{i-1}^{(3)}*K_i^{(4)})\oplus (A_i+C_i),$

где $K_i^{(j)}$ — j-й ключ на i-м раунде.

Формула для вычисления 9-го раунда:

$X_9^{(0)}=X_8^{(0)}*K_9^{(1)};$

$X_9^{(1)}=X_8^{(2)}+K_9^{(2)};$

$X_9^{(2)}=X_8^{(1)}+K_9^{(3)};$

$X_9^{(3)}=X_8^{(3)}*K_9^{(4)}.$

Выходом функции будет

$Y=\{X_9^{(0)}{X}_9^{(1)}{X}_9^{(2)}{X}_9^{(3)}\}.$

Можно заметить, что s- и p-блоки в чистом виде не используются. В качестве основных операций используются:

• умножение по модулю $2^{16}+1=65537$;
• сложение по модулю $2^{16}=65536$.

Шифры на основе сети Фейстеля

Люцифер (Lucifer)

Файл:S-chooser.png

Модуль, выбирающий используемую таблицу подстановок по битовому ключу

Файл:Lucifer v1.png

Упрощённая схема s- и p-слоёв в алгоритме «Люцифер» (июнь 1971)

Файл:Ones Propagation.png

Схема генерации и распространения единиц

Исторически первым алгоритмом, использующим сеть Фейстеля, был алгоритм «Люцифер», при работе над которым Фейстелем и была, собственно, разработана структура, впоследствии получившая название «сеть Фейстеля». В июне 1971 года Фейстелем был получен американский патент № 3798359.

Первая версия «Люцифера» использовала блоки и ключи длиной по 48 бит и не использовала конструкцию «сеть Фейстеля». Последующая модификация алгоритма была запатентована на имя Джона Л. Смитта (Шаблон:Lang-en) в ноябре 1971 года (US Patent 3,796,830; Nov 1971), и в патенте содержится как описание собственно самой «сети Фейстеля», так и конкретной функции шифрования. В ней использовались 64-разрядные ключи и 32-битные блоки. И, наконец, последняя версия предложена в 1973 году и оперировала с 128-битными блоками и ключами. Наиболее полное описание алгоритма «Люцифер» было приведено в статье Артура Соркина (Шаблон:Lang-en) «Люцифер. Криптографический алгоритм» («Lucifer, A Cryptographic Algorithm») в журнале «Криптология» («Cryptologia») за январь 1984.

Хотя изначальная модификация «Люцифера» обходилась без «ячеек Фейстеля», она хорошо демонстрирует то, как только применением s- и p-блоков можно сильно исказить исходный текст. Структура алгоритма «Люцифер» образца июня 1971 года представляет собой «сэндвич» из слоёв двух типов, используемых по очереди — так называемые SP-сети (или подстановочно-перестановочные сети). Первый тип слоя — p-блок разрядности 128 бит, за ним идёт второй слой, представляющий собой 32 модуля, каждый из которых состоит их двух четырёхбитных s-блоков, чьи соответствующие входы закорочены и на них подаётся одно и то же значение с выхода предыдущего слоя. Но сами блоки подстановок различны (отличаются таблицами замен). На выход модуля подаются значения только с одного из s-блоков, какого конкретно — определяется одним из битов в ключе, номер которого соответствовал номеру s-блока в структуре. Упрощённая схема алгоритма меньшей разрядности и неполным числом раундов приведена на рисунке. В ней используется 16 модулей выбора s-блоков (всего 32 s-блока), таким образом такая схема использует 16-битный ключ.

Рассмотрим теперь, как будет меняться шифротекст, в приведённом выше алгоритме, при изменении всего одного бита. Для простоты возьмём таблицы замен s-блоков такими, что если на вход s-блока подаются все нули, то и на выходе будут все нули. В силу нашего выбора s-блоков, если на вход шифрующего устройства подаются все нули, то и на выходе устройства будут все нули. В реальных системах такие таблицы замен не используются, так как они сильно упрощают работу криптоаналитика, но в нашем примере они наглядно иллюстрируют сильную межсимвольную взаимосвязь при изменении одного бита шифруемого сообщения. Видно, что благодаря первому p-блоку единственная единица сдвигается перемещается в центр блока, затем следующий нелинейный s-блок «размножает» её, и уже две единицы за счёт следующего p-блока изменяют своё положение и т. д. В конце устройства шифрования, благодаря сильной межсимвольной связи, выходные биты стали сложной функцией от входных и от используемого ключа. В среднем на выходе половина бит будет равна «0» и половина — «1».

По своей сути сеть Фейстеля является альтернативой сложным SP-сетям и используется намного шире. С теоретической точки зрения раундовая функция шифрования может быть сведена к SP-сети, однако сеть Фейстеля является более практичной, так как шифрование и дешифрование может вестись одним и тем же устройством, но с обратным порядком используемых ключей. Вторая и третья версия алгоритма (использующие сеть Фейстеля) оперировали над 32-битными блоками с 64-битным ключом и 128-битными блоками со 128-битными ключами. В последней (третьей) версии раундовая функция шифрования была устроена очень просто — сначала шифруемый подблок пропускался через слой 4-битных s-блоков (аналогично слоям в SP-сетях, только s-блок является константным и не зависит от ключа), затем к нему по модулю 2 добавлялся раундовый ключ, после чего результат пропускался через p-блок.

DES

Функция $f(L_i,K_i)$ (где:

• $L_i$ — 32-разрядный входной блок на i-й итерации;
• $K_i$ — 48-разрядный ключ на данной итерации)

в алгоритме DES состоит из следующих операций:

• расширение входного блока L до 48 разрядов (некоторые входные разряды могут повторяться);
• Сложение по модулю 2 с ключом $K_i$:

$\widetilde{L_i}=L_i\oplus K_i;$

• деление результата на 8 блоков длиной по 6 бит каждый:

$\widetilde{L_i}=\{{\widetilde{L_i}}^{(0)}{\widetilde{L_i}}^{(1)}{\widetilde{L_i}}^{(2)}{\widetilde{L_i}}^{(3)}{\widetilde{L_i}}^{(4)}{\widetilde{L_i}}^{(5)}{\widetilde{L_i}}^{(6)}{\widetilde{L_i}}^{(7)}\};$

• полученные блоки информации $\widetilde{L_i^{(j)}}$ подаются на блоки подстановок, имеющие 6-разрядные входы и 4-разрядные выходы;
• на выходе 4-битные блоки объединяются в 32-битный, который и является результатом функции $f(L_i,K_i)$.

Полное число раундов в алгоритме DES равно 16.

«Магма»

Функция $f(L_i,K_i)$ (где $L_i$ и $K_i$ — 32-битные числа) вычисляется следующим образом:

• складываются $L_i$ и $K_i$ по модулю $2^{32}$:

$\widetilde{L_i}=(L_i+K_i)mod{2}^{32};$

• результат разбивается на 8 4-битных блоков, которые подаются на вход 4-разрядных s-блоков (которые могут быть различными);
• выходы s-блоков объединяют в 32-битное число, которое затем сдвигается циклически на 11 битов влево;
• полученный результат является выходом функции.

Количество раундов в алгоритме ГОСТ 28147—89 равно 32.

Сравнительный список алгоритмов

Следующие блочные шифры в качестве своей основы используют классическую или модифицированную сеть Фейстеля.

Алгоритм	Год	Число раундов	Длина ключа	Размер блока	Количество подблоков
Blowfish	1993	16	от 32 до 448	64	2
Camellia	2000	18/24	128/192/256	128	2
CAST-128	1996	12/16	40-128	64	2
CAST-256	1998	12×4=48	128/192/256	128	2
CIPHERUNICORN-A	2000	16	128/192/256	128	2
CIPHERUNICORN-E	1998	16	128	64	2
CLEFIA	2007	16	128/192/256	128	16
DEAL	1998	6 (8)	(128/192) 256	128	2
DES	1977	16	56	64	2
DFC	1998	8	128/192/256	128	?
FEAL	1987	4-32	64	64	2
ГОСТ 28147-89	1989	32/16	256	64	2
IDEA	1991	8+1	128	64	4
KASUMI	1999	8	128	64	2
Khufu	1990	16-32/64	512	64	2
LOKI97	1997	16	128/192/256	128	2
Lucifer	1971	16	48/64/128	48/32/128	2
MacGuffin	1994	32	128	64	4
MAGENTA	1998	6/8	128/192/256	128	2
MARS	1998	32	128—1248	128	2
Mercy	2000	6	128	4096	?
MISTY1	1995	4×n(8)	128	64	4
Raiden	2006	16	128	64	2
RC2	1987	16+2	8-128	64	4
RC5	1994	1-255(12)	0-2040(128)	32/64/128	2
RC6	1998	20	128/192/256	128	4
RTEA	2007	48/64	128/256	64	2
SEED	1998	16	128	128	2
Sinople	2003	64	128	128	4
Skipjack	1998	32	80	64	4
TEA	1994	64	128	64	2
Triple DES	1978	32/48	112/168	64	2
Twofish	1998	16	128/192/256	128	4
XTEA	1997	64	128	64	2
XTEA-3	1999	64	256	128	4
XXTEA	1998	12-64	128	64	2

Литература

• Шаблон:Source
• Шаблон:Source