Тестовые функции для оптимизации

В прикладной математике, тестовые функции, известные как искусственные ландшафты, являются полезными для оценки характеристик алгоритмов оптимизации, таких как:

• Скорость сходимости.
• Точность.
• Робастность.
• Общая производительность.

В статье представлены некоторые тестовые функции с целью дать представление о различных ситуациях, с которыми приходится сталкиваться при преодолении подобных проблем.

В статье представлены общая формула уравнения, участок целевой функции, границы переменных и координаты глобального минимума.

Тестовые функции для одной цели оптимизации

Название	Рисунок	Формула	Глобальный минимум	Метод поиска
Функция Растригина		$f(𝐱)=An+\sum _{i=1}^n[x_i^2-A\cos (2\pi x_i)]$ $\text{where: }A=10$	$f(0,\dots ,0)=0$	$-5.12\le x_i\le 5.12$
Шаблон:Нп3		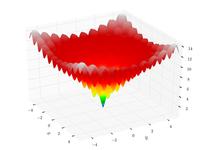$f(x,y)=-20\exp [-0.2\sqrt{0.5(x^2+y^2)}]$ $-\exp [0.5(\cos (2\pi x)+\cos (2\pi y))]+e+20$	$f(0,0)=0$	$-5\le x,y\le 5$
Функция сферы		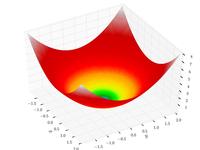$f(𝒙)=\sum _{i=1}^n{x}_i^2$	$f(x_1,\dots ,x_n)=f(0,\dots ,0)=0$	$-\mathrm{\infty }\le x_i\le \mathrm{\infty }$, $1\le i\le n$
Функция Розенброка		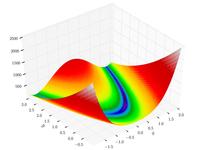$f(𝒙)=\sum _{i=1}^{n-1}[100{(x_{i+1}-x_i^2)}^2+{(x_i-1)}^2]$	$\text{Min}=\{\begin{array}{cc}n=2& \to f(1,1)=0,\\ n=3& \to f(1,1,1)=0,\\ n>3& \to f(\underset{n\text{ times}}{\underbrace{1,\dots ,1}})=0\end{array}$	$-\mathrm{\infty }\le x_i\le \mathrm{\infty }$, $1\le i\le n$
Функция Била		$f(x,y)={(1.5-x+xy)}^2+{(2.25-x+x{y}^2)}^2$ $+{(2.625-x+x{y}^3)}^2$	$f(3,0.5)=0$	$-4.5\le x,y\le 4.5$
Функция Гольдшейна-Прайса		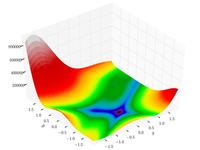$f(x,y)=[1+{(x+y+1)}^2(19-14x+3x^2-14y+6xy+3y^2)]$ $[30+{(2x-3y)}^2(18-32x+12x^2+48y-36xy+27y^2)]$	$f(0,-1)=3$	$-2\le x,y\le 2$
Функция Бута		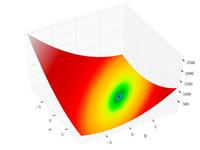$f(x,y)={(x+2y-7)}^2+{(2x+y-5)}^2$	$f(1,3)=0$	$-10\le x,y\le 10$
Функция Букина N 6		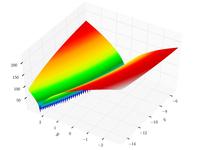$f(x,y)=100\sqrt{|y-0.01x^2|}+0.01|x+10|.$	$f(-10,1)=0$	$-15\le x\le -5$, $-3\le y\le 3$
Функция Матьяса		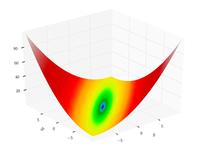$f(x,y)=0.26(x^2+y^2)-0.48xy$	$f(0,0)=0$	$-10\le x,y\le 10$
Функция Леви N 13		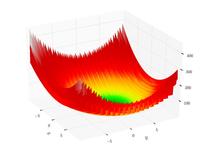$f(x,y)={\sin }^{2}3\pi x+{(x-1)}^2(1+{\sin }^{2}3\pi y)$ $+{(y-1)}^2(1+{\sin }^{2}2\pi y)$	$f(1,1)=0$	$-10\le x,y\le 10$
Функция Химмельблау		$f(x,y)=(x^2+y-11{)}^2+(x+y^2-7{)}^2.$	$\text{Min}=\{\begin{array}{cc}f(3.0,2.0)& =0.0\\ f(-2.805118,3.131312)& =0.0\\ f(-3.779310,-3.283186)& =0.0\\ f(3.584428,-1.848126)& =0.0\end{array}$	$-5\le x,y\le 5$
Функция трехгорбого верблюда		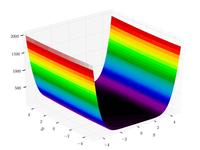$f(x,y)=2x^2-1.05x^4+\frac{x^6}{6}+xy+y^2$	$f(0,0)=0$	$-5\le x,y\le 5$
Функция Изома		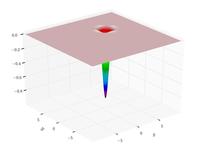$f(x,y)=-\cos \left(x\right)\cos \left(y\right)\exp (-({(x-\pi )}^2+{(y-\pi )}^2))$	$f(\pi ,\pi )=-1$	$-100\le x,y\le 100$
Функция "крест на подносе" (Cross-in-tray function)		$f(x,y)=-0.0001{[|\sin x\sin y\exp \left(|100-\frac{\sqrt{x^2+y^2}}{\pi }|\right)|+1]}^{0.1}$	$\text{Min}=\{\begin{array}{cc}f(1.34941,-1.34941)& =-2.06261\\ f(1.34941,1.34941)& =-2.06261\\ f(-1.34941,1.34941)& =-2.06261\\ f(-1.34941,-1.34941)& =-2.06261\end{array}$	$-10\le x,y\le 10$
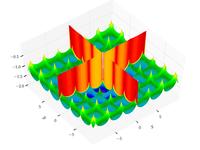
Функция "подставка для яиц" (Eggholder function)		$f(x,y)=-(y+47)\sin \sqrt{|\frac{x}{2}+(y+47)|}-x\sin \sqrt{|x-(y+47)|}$	$f(512,404.2319)=-959.6407$	$-512\le x,y\le 512$
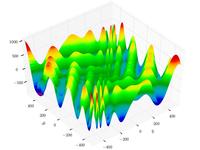
Табличная функция Хольдера		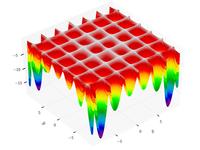$f(x,y)=-|\sin x\cos y\exp \left(|1-\frac{\sqrt{x^2+y^2}}{\pi }|\right)|$	$\text{Min}=\{\begin{array}{cc}f(8.05502,9.66459)& =-19.2085\\ f(-8.05502,9.66459)& =-19.2085\\ f(8.05502,-9.66459)& =-19.2085\\ f(-8.05502,-9.66459)& =-19.2085\end{array}$	$-10\le x,y\le 10$
Функция МакКормика		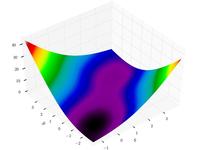$f(x,y)=\sin (x+y)+{(x-y)}^2-1.5x+2.5y+1$	$f(-0.54719,-1.54719)=-1.9133$	$-1.5\le x\le 4$, $-3\le y\le 4$
Функция Шаффера N2		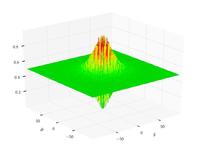$f(x,y)=0.5+\frac{{\sin }^2(x^2-y^2)-0.5}{{[1+0.001(x^2+y^2)]}^2}$	$f(0,0)=0$	$-100\le x,y\le 100$
Функция Шаффера N4		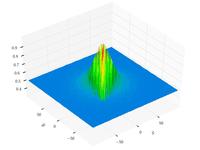$f(x,y)=0.5+\frac{{\cos }^2[\sin \left(|x^2-y^2|\right)]-0.5}{{[1+0.001(x^2+y^2)]}^2}$	$f(0,1.25313)=0.292579$	$-100\le x,y\le 100$
Функция Стыбинского-Танга		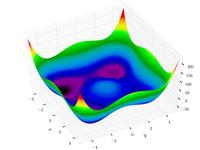$f(𝒙)=\frac{\sum _{i=1}^n{x}_i^4-16x_i^2+5x_i}{2}$	$-39.16617n<f(\underset{n\text{ times}}{\underbrace{-2.903534,\dots ,-2.903534}})<-39.16616n$	$-5\le x_i\le 5$, $1\le i\le n$..

Тестовые функции для условной оптимизации

Название	Рисунок	Формула	Глобальный минимум	Метод поиска
функция Розенброка, ограничена кубической и прямой		$f(x,y)=(1-x{)}^2+100(y-x^2{)}^2$, subjected to: $(x-1{)}^3-y+1<0\text{ and }x+y-2<0$	$f(1.0,1.0)=0$	$-1.5\le x\le 1.5$, $-0.5\le y\le 2.5$
Функция Розенброка, ограниченная диском		$f(x,y)=(1-x{)}^2+100(y-x^2{)}^2$, subjected to: $x^2+y^2<2$	$f(1.0,1.0)=0$	$-1.5\le x\le 1.5$, $-1.5\le y\le 1.5$
Ограниченная функция Мишры-Бёрда		$f(x,y)=\sin (y)e^{[(1-\cos x{)}^2]}+\cos (x)e^{[(1-\sin y{)}^2]}+(x-y{)}^2$, subjected to: $(x+5{)}^2+(y+5{)}^2<25$	$f(-3.1302468,-1.5821422)=-106.7645367$	$-10\le x\le 0$, $-6.5\le y\le 0$
Модифицированная функция Таусенда		$f(x,y)=-[\cos ((x-0.1)y){]}^2-x\sin (3x+y)$, subjected to:$x^2+y^2<{[2\cos t-\frac{1}{2}\cos 2t-\frac{1}{4}\cos 3t-\frac{1}{8}\cos 4t]}^2+[2\sin t{]}^2$ where: Шаблон:Math	$f(2.0052938,1.1944509)=-2.0239884$	$-2.25\le x\le 2.5$, $-2.5\le y\le 1.75$
Функция Симионеску		$f(x,y)=0.1xy$, subjected to: $x^2+y^2\le {[r_T+r_S\cos (n\arctan \frac{x}{y})]}^2$ $\text{where: }{r}_T=1,r_S=0.2\text{ and }n=8$	$f(\pm 0.85586214,\mp 0.85586214)=-0.072625$	$-1.25\le x,y\le 1.25$

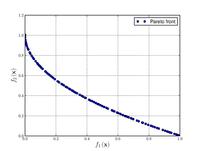
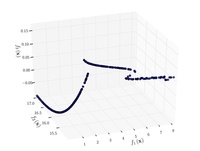
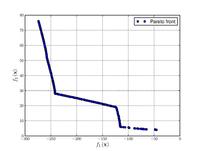
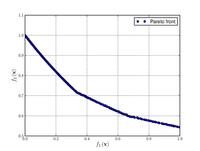
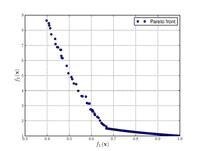
Тестовые функции для многокритериальной оптимизации

Название / Рисунок	Формула	Минимум	Область поиска
Функция Бина и Корна	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =4x^2+4y^2\\ f_2(x,y)& ={(x-5)}^2+{(y-5)}^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& ={(x-5)}^2+y^2\le 25\\ g_2(x,y)& ={(x-8)}^2+{(y+3)}^2\ge 7.7\end{array}$	$0\le x\le 5$, $0\le y\le 3$
Chakong and Haimes function	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =2+{(x-2)}^2+{(y-1)}^2\\ f_2(x,y)& =9x-{(y-1)}^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =x^2+y^2\le 225\\ g_2(x,y)& =x-3y+10\le 0\end{array}$	$-20\le x,y\le 20$
Функция Фонсеки и Флеминга	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =1-\exp (-\sum _{i=1}^n{(x_i-\frac{1}{\sqrt{n}})}^2)\\ f_2\left(𝒙\right)& =1-\exp (-\sum _{i=1}^n{(x_i+\frac{1}{\sqrt{n}})}^2)\end{array}$		$-4\le x_i\le 4$, $1\le i\le n$
Test function 4	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x^2-y\\ f_2(x,y)& =-0.5x-y-1\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =6.5-\frac{x}{6}-y\ge 0\\ g_2(x,y)& =7.5-0.5x-y\ge 0\\ g_3(x,y)& =30-5x-y\ge 0\end{array}$	$-7\le x,y\le 4$
Функция Курсаве	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =\sum _{i=1}^2[-10\exp (-0.2\sqrt{x_i^2+x_{i+1}^2})]\\ & \\ f_2\left(𝒙\right)& =\sum _{i=1}^3[{\left|x_i\right|}^{0.8}+5\sin \left(x_i^3\right)]\end{array}$		$-5\le x_i\le 5$, $1\le i\le 3$.
Schaffer function N. 1	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(x\right)& =x^2\\ f_2\left(x\right)& ={(x-2)}^2\end{array}$		$-A\le x\le A$. Values of $A$ form $10$ to $10^5$ have been used successfully. Higher values of $A$ increase the difficulty of the problem.
Schaffer function N. 2	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(x\right)& =\{\begin{array}{cc}-x,& \text{if }x\le 1\\ x-2,& \text{if }1<x\le 3\\ 4-x,& \text{if }3<x\le 4\\ x-4,& \text{if }x>4\end{array}\\ f_2\left(x\right)& ={(x-5)}^2\end{array}$		$-5\le x\le 10$.
Объективная функция Полони2	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =[1+{(A_1-B_1(x,y))}^2+{(A_2-B_2(x,y))}^2]\\ f_2(x,y)& ={(x+3)}^2+{(y+1)}^2\end{array}$ $\text{where}=\{\begin{array}{cc}{A}_1& =0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\ A_2& =1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\ B_1(x,y)& =0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\ B_2(x,y)& =1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{array}$		$-\pi \le x,y\le \pi$
Функция Зистера-Дьеба-Тери N. 1	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Функция Зистера-Дьеба-Тери N. 2	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-{\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)}^2\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Функция Зистера-Дьеба-Териn N. 3	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+\frac{9}{29}\sum _{i=2}^{30}{x}_i\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}-\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)\sin \left(10\pi f_1\left(𝒙\right)\right)\end{array}$		$0\le x_i\le 1$, $1\le i\le 30$.
Функция Зистера-Дьеба-ТериN. 4	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =x_1\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =91+\sum _{i=2}^{10}(x_i^2-10\cos \left(4\pi x_i\right))\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-\sqrt{\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}}\end{array}$		$0\le x_1\le 1$, $-5\le x_i\le 5$, $2\le i\le 10$
Функция Зистера-Дьеба-Тери N. 6	$\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =1-\exp (-4x_1){\sin }^6\left(6\pi x_1\right)\\ f_2\left(𝒙\right)& =g\left(𝒙\right)h(f_1\left(𝒙\right),g\left(𝒙\right))\\ g\left(𝒙\right)& =1+9{\left[\frac{\sum _{i=2}^{10}{x}_i}{9}\right]}^{0.25}\\ h(f_1\left(𝒙\right),g\left(𝒙\right))& =1-{\left(\frac{f_1\left(𝒙\right)}{g\left(𝒙\right)}\right)}^2\end{array}$		$0\le x_i\le 1$, $1\le i\le 10$.
Функция Виннета	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =0.5(x^2+y^2)+\sin (x^2+y^2)\\ f_2(x,y)& =\frac{{(3x-2y+4)}^2}{8}+\frac{{(x-y+1)}^2}{27}+15\\ f_3(x,y)& =\frac{1}{x^2+y^2+1}-1.1\exp (-(x^2+y^2))\end{array}$		$-3\le x,y\le 3$.
Функция Осызки и Кунду	$F_1(x)=-25{(x_1-2)}^2-{(x_2-2)}^2$ $-{(x_3-1)}^2-{(x_4-4)}^2-{(x_5-1)}^2$ $\text{Minimize}=\{\begin{array}{cc}{f}_1\left(𝒙\right)& =F_1(x)\\ f_2\left(𝒙\right)& =\sum _{i=1}^6{x}_i^2\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1\left(𝒙\right)& =x_1+x_2-2\ge 0\\ g_2\left(𝒙\right)& =6-x_1-x_2\ge 0\\ g_3\left(𝒙\right)& =2-x_2+x_1\ge 0\\ g_4\left(𝒙\right)& =2-x_1+3x_2\ge 0\\ g_5\left(𝒙\right)& =4-{(x_3-3)}^2-x_4\ge 0\\ g_6\left(𝒙\right)& ={(x_5-3)}^2+x_6-4\ge 0\end{array}$	$0\le x_1,x_2,x_6\le 10$, $1\le x_3,x_5\le 5$, $0\le x_4\le 6$.
CTP1 function (2 variables)	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x\\ f_2(x,y)& =(1+y)\exp (-\frac{x}{1+y})\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =\frac{f_2(x,y)}{0.858\exp (-0.541f_1(x,y))}\ge 1\\ g_1(x,y)& =\frac{f_2(x,y)}{0.728\exp (-0.295f_1(x,y))}\ge 1\end{array}$	$0\le x,y\le 1$.
Проблема Констр-Экса	$\text{Minimize}=\{\begin{array}{cc}{f}_1(x,y)& =x\\ f_2(x,y)& =\frac{1+y}{x}\end{array}$	$\text{s.t.}=\{\begin{array}{cc}{g}_1(x,y)& =y+9x\ge 6\\ g_1(x,y)& =-y+9x\ge 1\end{array}$	$0.1\le x\le 1$, $0\le y\le 5$

См. также

• Функция Химмельблау
• Функция Растригина
• Функция Розенброка

Литература

• Пантелеев А. В., Метлицкая Д. В., Е.А. Алешина Методы глобальной оптимизации. Метаэвристические стратегии и алгоритмы // М.: Вузовская книга. 2013. 244 с. ISBN 978-5-9502-0743-3
• Сергиенко А. Б. Тестовые функции для глобальной оптимизации.

Ссылки

• Тестирование алгоритмов многомерной оптимизации