Брахистохрона

Брахистохро́на (от Шаблон:Lang-el «кратчайший» + Шаблон:Lang-el2 «время») — кривая скорейшего спуска. Задача о её нахождении была поставлена в июне 1696 года Иоганном Бернулли следующим образом: Шаблон:Рамка Среди плоских кривых, соединяющих две данные точки $A$ и $B$, лежащих в одной вертикальной плоскости ($B$ ниже $A$), найти ту, двигаясь по которой под действием только силы тяжести, сонаправленной отрицательной полуоси $OY$, материальная точка из $A$ достигнет $B$ за кратчайшее время. Шаблон:Конец рамки

Решением задачи о брахистохроне является дуга циклоиды с горизонтальным основанием, точка возврата которой находится в точке $A$, или иными словами, имеющая вертикальную касательную в точке $A$.

Примечательно, что время спуска до нижней точки не зависит от расположения начальной точки на дуге циклоиды.

Решение задачи о брахистохроне

Движение тел по различным траекториям. Красная линия — брахистохрона

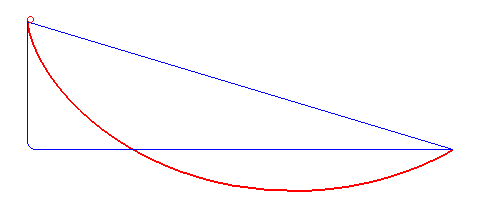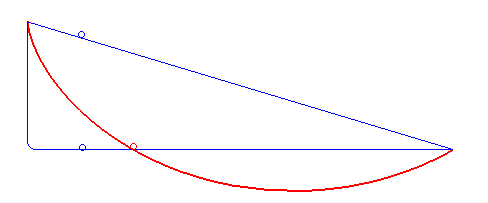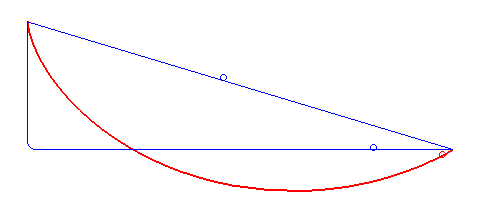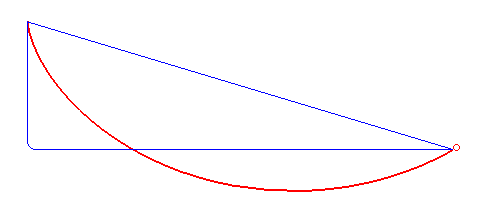
На статью Иоганна Бернулли откликнулись Исаак Ньютон, Якоб Бернулли, Г. В. Лейбниц, Г. Ф. Лопиталь, Э. В. Чирнхаус. Все они, как и сам Иоганн Бернулли, решили задачу разными способами. Метод решения, полученного 26 января 1697 года Исааком Ньютоном, лёг в основу важнейшей области естествознания — вариационного исчисления.

Пусть имеются две произвольные точки, расположенные на разных ординатах. Далее пусть произвольная материальная точка M скатывается от точки A к точке B под действием только силы тяжести (силы трения отсутствуют). Найдём такую траекторию, при которой время скатывания будет минимально.

Направим ось ординат вниз и сопоставим начальной точке нулевое значение ординаты. Запишем закон сохранения энергии для материальной точки M:

$\frac{m{v}^2}{2}=mgy,$

где

$m$ — масса тела,

$g$ — ускорение свободного падения,

$y$ — ордината,

$v$ — скорость движения тела.

Получаем:

$v=\sqrt{2gy},$

откуда можно найти значение проекции скорости на ось $x$:

$v_x=\frac{v}{\sqrt{1+(y^{\prime }{)}^2}}=\frac{\sqrt{2gy}}{\sqrt{1+(y^{\prime }{)}^2}}.$

Поскольку время на спуск равняется $\underset{a}{\overset{b}{\int }}\frac{1}{v_x}dx$, то задача сводится к минимизации значения интеграла

$\frac{1}{\sqrt{2g}}\underset{a}{\overset{b}{\int }}\sqrt{\frac{1+(y^{\prime }{)}^2}{y}}dx.$

Литература

• Шаблон:ВТ-ЭСБЕ

Ссылки

• Страница с Java-апплетом, строящим брахистохрону и анимирующим движение по ней
• Решение Я. Бернулли задачи о брахистохроне