Граф пересечений

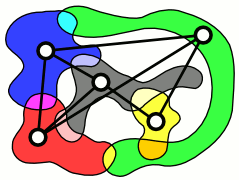
В теории графов графом пересечений называется граф, Шаблон:Не переведено 5 схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.

Обзор теории графов пересечений и важных специальных классов графов пересечений смотрите в книге МакКи и МакМоррисаШаблон:Sfn.

Формальное определение

Граф пересечений — это неориентированный граф, образованный из семейства множеств

$S_i,i=0,1,2,...$

путём создания вершины $v_i$ для каждого множества $S_i$ и соединения двух вершин $v_i$ и $v_j$ ребром, если соответствующие два множества имеют непустое пересечение, то есть

$E(G)=\{\{v_i,v_j\}|S_i\cap S_j\ne \mathrm{\varnothing }\}$.

Все графы являются графами пересечений

Любой неориентированный граф G можно представить как граф пересечений — для любой вершины $v_i$ графа G образуем множество $S_i$, состоящее из рёбер, инцидентных $v_i$. Два таких множества имеют непустое пересечение тогда и только тогда, когда соответствующие вершины принадлежат одному ребру. Эрдёш, Гудман и ПозаШаблон:Sfn показали более эффективное построение (которое требует меньше элементов во всех множествах $S_i$), в котором общее число элементов в множествах не превосходит $n^2/4$, где n — число вершин в графе. Он приписывают наблюдение, что все графы являются графами пересечений, МарчевскомуШаблон:Sfn, но также рекомендуют посмотреть работы ЧуликаШаблон:Sfn. Число пересечений графа — это минимальное число элементов в представлениях графа, как графа пересечений.

Классы графов пересечений

Много важных семейств графов можно описать как графы пересечений ограниченных типов множеств, например, множеств, полученных из некоторых геометрических конфигураций:

• Интервальный граф определяется как граф пересечений интервалов на прямой, или связных подграфов-путей.
• Граф дуг окружности определяется как граф пересечений дуг окружности.
• Граф многоугольников на окружности определяется как граф пересечений многоугольников с вершинами, лежащими на окружности.
• Одна из характеристик хордальных графов — это то, что они являются графами пересечений связных подграфов дерева.
• Трапецеидальный граф определяется как граф пересечений трапеций, образованных двумя параллельными прямыми. Они являются обобщением понятия графа перестановки, которые, в свою очередь, являются специальным случаем семейства дополнений графов сравнимости, известных как графы косравнимости.
• Граф единичных кругов определяется как граф пересечений единичных кругов на плоскости.
• Теорема об упаковке кругов утверждает, что планарные графы — это в точности графы пересечений семейств замкнутых непересекающихся (разрешено касание) дисков на плоскости.
• Гипотеза Шейнермана (теперь — теорема) утверждает, что любой планарный граф можно представить в виде графа пересечений отрезков на плоскости. Однако графы пересечений отрезков на прямой могут быть непланарными, и распознавание графов пересечений отрезков на прямой является Шаблон:Не переведено 5 для теории существования вещественных чиселШаблон:Sfn.
• Рёберный граф графа G определяется как граф пересечений рёбер графа G, где каждое ребро рассматривается как множество из двух его конечных вершин.
• Струнный граф — это граф пересечений кривых на плоскости.
• Граф имеет рамочность k, если он является графом пересечений многомерных прямоугольников размерности k, но не меньших размерностей.

Вариации и обобщения

• Теоретическими аналогами порядка графов пересечений служат Шаблон:Не переведено 5. Точно таким же образом, каким представление графа пересечений помечает каждую вершину множеством инцидентных ей рёбер, имеющих непустое пересечение, представление порядка вложенности f частично упорядоченного множества помечает каждый элемент таким множеством, что для любого x и y в нём $x\le y$ тогда и только тогда, когда $f(x)\subseteq f(y)$.
• Нерв покрытия

Литература

• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Книга

Ссылки

• Jan Kratochvíl, A video lecture on intersection graphs (June 2007) Шаблон:Wayback
• E. Prisner, A Journey through Intersection Graph County Шаблон:Wayback