Моноидальный функтор

В теории категорий моноидальные функторы — это функторы между моноидальными категориями, сохраняюющие моноидальную структуру, то есть умножение и тождественный элемент.

Определение

Пусть $(𝒞,\otimes ,I_{𝒞})$ и $(𝒟,\bullet ,I_{𝒟})$ — моноидальные категории. Моноидальный функтор из $𝒞$ в $𝒟$ состоит из функтора $F:𝒞\to 𝒟$, естественного преобразования

${\varphi }_{A,B}:FA\bullet FB\to F(A\otimes B)$

и морфизма

$\varphi :I_{𝒟}\to F{I}_{𝒞}$,

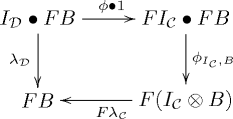
называемых структурными морфизмами, таких что для любых $A$, $B$, $C$ в $𝒞$ диаграммы

   и   

коммутативны в категории $𝒟$. Здесь используются стандартные обозначения $\alpha ,\rho ,\lambda$ для моноидальной структуры категорий $𝒞$ и $𝒟$.

Сильно моноидальный функтор — это моноидальный функтор, такой что структурные морфизмы ${\varphi }_{A,B},\varphi$ обратимы.

Строго моноидальный функтор — это моноидальный функтор, структурные морфизмы которого тождественны.

Пример

Забывающий функтор $U:(𝐀𝐛,{\otimes }_{𝐙},𝐙)\to (𝐒𝐞𝐭,\times ,\{*\})$ из категории абелевых групп в категорию множеств. Здесь структурный морфизм ${\varphi }_{A,B}:U(A)\times U(B)\to U(A\otimes B)$ — это сюръекция, индуцированная стандартным отображением $A\times B\to A\otimes B\to$; отображение $\varphi :\{*\}\to \mathbb{Z}$ переводит синглетон * в 1.

Примечания

• Kelly, G. Max (1974), «Doctrinal adjunction», Lecture Notes in Mathematics, 420, 257—280