Оценка эффективности инвестиционного портфеля

Оценка эффективности инвестиционного портфеля (Шаблон:Lang-en) — составляющая инвестиционного процесса, заключающаяся в периодическом анализе функционирования инвестиционного портфеля в терминах доходности и риска

С точки зрения рисков, наилучшим вложением денежных средств является приобретение государственных облигаций, обеспечивающих безрисковую процентную ставку, однако отсутствие риска сказывается и на уровне доходности, редко покрывающем убытки, связанные с инфляционными процессами. Несмотря на это, безрисковая процентная ставка является бенчмарком для оценки эффективности любого типа инвестиционных стратегий.

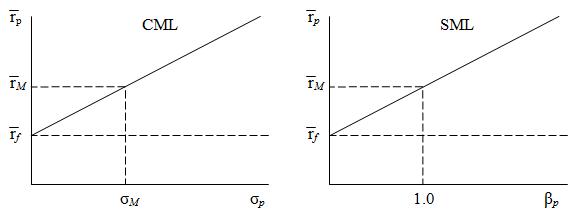
Согласно модели оценки финансовых активов CAPM (Шаблон:Lang-en), взаимосвязь между риском и доходностью определяется посредством Рыночной линии CML (Шаблон:Lang-en) и Рыночной линии ценной бумаги SML (Шаблон:Lang-en), ключевую роль в которых играет безрисковая процентная ставка и доходность рыночного индекса.

Основными мерами риска инвестиций в финансовые активы принято считать стандартное отклонение и Бета-коэффициент, на основании которых и строятся CML и SML. Данные линии есть не что иное, как доходность эталонного портфеля, в зависимости от стандартного отклонения и Бета-коэффициента.

Где:

$\bar{r}$_f — средняя безрисковая процентная ставка;

$\bar{r}$_M — средняя доходность рыночного индекса;

$\bar{r}$_p — средняя доходность инвестиционного портфеля;

σ_M — стандартное отклонение доходности рыночного индекса;

σ_p — стандартное отклонение доходности инвестиционного портфеля;

β_p — Бета-коэффициент инвестиционного портфеля;

Оценка инвестиционного портфеля происходит по следующему принципу — если его доходность находится выше линий CML и SML, то он считается более эффективным, чем эталонный портфель. И наоборот, инвестиционный портфель, доходность которого находится ниже линий CML и SML, будет считаться неэффективным ввиду получения заниженной доходности при повышенном уровне риска.

Для того чтобы формализовать процесс сравнения инвестиционного портфеля с эталонным портфелем, необходимо вывести ряд коэффициентов. Для этого необходимо представить в виде формулы линию SML:

${\bar{r}}_p^e={\bar{r}}_f+({\bar{r}}_M-{\bar{r}}_f){\beta }_p$

Где:

$\bar{r}$_p^e — средняя доходность эталонного портфеля;

$\bar{r}$_M — средняя доходность рыночного индекса;

$\bar{r}$_f — средняя безрисковая процентная ставка;

β_p — Бета-коэффициент инвестиционного портфеля;

Затем нужно представить в виде формулы линию CML:

${\bar{r}}_p^e={\bar{r}}_f+\frac{({\bar{r}}_M-{\bar{r}}_f)}{{\sigma }_M}{\sigma }_p$

Где:

σ_M — стандартное отклонение рыночного индекса;

σ_p — стандартное отклонение инвестиционного портфеля;

Первым показателем, выступающим мерой эффективности портфеля, является Коэффициент Трейнора RVOL (Шаблон:Lang-en), рассчитываемый как отношение избыточной доходности портфеля, по сравнению с безрисковой процентной ставкой, к рыночному риску портфеля (Бета-коэффициенту):

$RVOL=\frac{{\bar{r}}_p-{\bar{r}}_f}{{\beta }_p}$

Вторым мерилом эффективности инвестиционного портфеля является Коэффициент Шарпа RVAR (Шаблон:Lang-en), рассчитываемый как отношение избыточной доходности портфеля, по сравнению с безрисковой процентной ставкой, к общему риску портфеля(стандартному отклонению доходности):

$RVAR=\frac{{\bar{r}}_p-{\bar{r}}_f}{{\sigma }_p}$

В первую очередь, эти коэффициенты рассчитываются для эталонного портфеля, с целью получения эталонных коэффициентов для заданных уровней рыночного и общего риска инвестиционного портфеля. После этого производится расчет коэффициентов непосредственно для инвестиционного портфеля.

Инвестиционный портфель считается эффективным, если:

RVOL > RVOL^e и RVOL > 0

RVAR > RVAR^e и RVAR > 0 (при β>0)

RVAR < RVAR^e и RVAR < 0 (при β<0)

Где:

RVOL — коэффициент Трейнора инвестиционного портфеля;

RVOL^e — коэффициент Трейнора эталонного портфеля;

RVAR — коэффициент Шарпа инвестиционного портфеля;

RVAR^e — коэффициент Шарпа эталонного портфеля;

См. также

• Портфельные инвестиции
• Бета-нейтральный портфель
• Портфельная теория Марковица