Эпициклоида

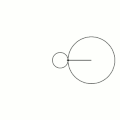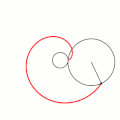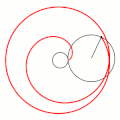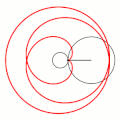
Эпицикло́ида (от Шаблон:Lang-grc — на, над, при и Шаблон:Lang-grc2 — круг, окружность) — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.

По свидетельству Лейбница, Оле Рёмер ранее 1676 года сделал важное в практическом отношении открытие, что эпициклоидические зубцы в зубчатом колесе производят наименьшее трение.

Уравнения

Если центр неподвижной окружности находится в начале координат, её радиус равен $R$, радиус катящейся по ней окружности равен $r$, то эпициклоида описывается параметрическими уравнениями относительно $\phi$:

$\{\begin{array}{c}x=(R+r)\cos \phi -r\cos (\alpha +\frac{R+r}{r}\phi )\\ y=(R+r)\sin \phi -r\sin (\alpha +\frac{R+r}{r}\phi )\end{array}$

где $\alpha$ — угол поворота точки, описывающей эпициклоиду, относительно центра подвижной окружности в момент начала движения (против часовой стрелки от оси x), $\phi$ — параметр, но фактически это угол наклона отрезка между центрами к оси $OX$.

Можно ввести величину $k=\frac{R}{r}$, тогда уравнения предстанут в виде

$\{\begin{array}{c}x=r(k+1)(\cos \phi -\frac{\cos ((k+1)\phi )}{k+1})\\ y=r(k+1)(\sin \phi -\frac{\sin ((k+1)\phi )}{k+1})\end{array}$

Величина $k$ определяет форму эпициклоиды. При $k=1$ эпициклоида образует кардиоиду, а при $k=2$ — нефроиду. Если $k$ — несократимая дробь вида $\frac{m}{n}$ ($m,n\in \mathbb{N}$), то $m$ — это количество каспов данной эпициклоиды, а $n$ — количество полных вращений катящейся окружности. Если $k$ иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.

• Эпициклоиды при разных значениях параметра k:
• 
  $k=1$ (кардиоида)
• 
  $k=2$ (нефроида)
• 
  $k=3$
• 
  $k=\frac{3}{4}$
• 
  $k=\frac{1}{3}$
• 
  $k=0.5=\frac{1}{2}$
• 
  $k=2.1=\frac{21}{10}$
• 
  $k=3.8=\frac{19}{5}$
• 
  $k=5.5=\frac{11}{2}$
• 
  $k=7.2=\frac{36}{5}$

Получение

Эскиз для доказательства

Пусть $P$ - искомая точка, $\alpha$ - угол отклонения точки $P$ от точки касания двух окружностей, $\theta$ - угол отклонения между центрами данных окружностей.

Так как окружность катится без скольжения, то ${\ell }_R={\ell }_r$

По определению длины дуги окружности:

${\ell }_R=\theta R\wedge {\ell }_r=\alpha r$

Из данных двух утверждений выплывает, что

$\theta R=\alpha r$

Получаем соотношения для $\alpha$:

$\alpha =\frac{R}{r}\theta$

Пусть центр неподвижной окружности $A$, центр второй окружности $B$. Очевидно, что $\overrightarrow{AB}+\overrightarrow{BP}=\overrightarrow{AP}$

Перепишем в координатах:

$\overrightarrow{AP}=\overrightarrow{((R+r)\cos \theta ;(R+r)\sin \theta )}+\overrightarrow{(r\cos (\pi +\theta +\alpha );r\sin (\pi +\theta +\alpha ))}=\overrightarrow{((R+r)\cos \theta -r\cos (\theta +\alpha );(R+r)\sin \theta -r\sin (\theta +\alpha ))}$

Следовательно позиция точки $p$:

$x=(R+r)\cos \theta -r\cos (\theta +\alpha )=(R+r)\cos \theta -r\cos \left(\frac{R+r}{r}\theta \right)$

$y=(R+r)\sin \theta -r\sin (\theta +\alpha )=(R+r)\sin \theta -r\sin \left(\frac{R+r}{r}\theta \right)$

См. также

• Циклоида
• Гипоциклоида
• Эпитрохоида