JH

JH — семейство из четырёх криптографических хеш-функций: JH-224, JH-256, JH-384 и JH-512.

Алгоритмы этих хеш-функций отличаются только значением одного внутреннего параметра — длины (в битах) $l_{hash}$ выходного значения (которая и указана после дефиса в названии). Далее в статье при описании алгоритма я буду считать этот параметр частью входных данных для удобства, говоря о JH, как об одном алгоритме или одной хеш-функции.

Хеш-функция JH входит в пятёрку финалистов второго тура SHA-3. В процессе этого конкурса она была улучшена. В статье рассматривается последняя на данный момент версия, которую также можно назвать JH42 (так как главное изменение состояло в том, что число раундов в функции компрессии стало равно 42). Дата выхода документации по ней — 16 января 2011 года.

При хешировании входное сообщение дополняется и разделяется на части, которые далее последовательно обрабатываются так называемой функцией компрессии. Эта функция описана в спецификации в общем виде — то есть с переменным параметром d, меняя который можно конструировать JH-подобные хеш-функции (тем более криптостойкие, чем больше d). В JH исходно d=8.

При выборе финалиста в конкурсе SHA решающую роль играют не криптографические характеристики (они у всех функций отличные), а гибкость и оптимальность в программной и аппаратной реализации. На тему аппаратной реализации существует много исследований, например.

Алгоритм

Уточнения

О названии элементов битовых векторов

Будем считать, что у всех обсуждаемых тут битовых векторов есть начало и конец, причём бит, расположенный в начале (слева) является первым, имеет позицию 0 и считается наиболее значимым, соответственно, бит, расположенный в конце (справа), является последним, имеет позицию с наибольшим номером, на один меньшим, чем число разрядов вектора, и считается наименее значимым.

То же самое, за исключением номера позиции, будем подразумевать для векторов, состоящих из битовых векторов, например, для сообщения, состоящего из блоков, или блока, состоящего из полубайтов. С номером же позиции какой-либо составной части битового вектора, состоящей из нескольких бит, будет путаница, создаваемая для удобства. Так, номера позиций полубайтов в блоке будут начинаться с нуля, а номера позиций блоков в сообщении — с единицы…

Шаблон:Скрытый

Обозначение конкатенации

Пусть вектор $A$ состоит из последовательно идущих векторов $A_1,A_2,\dots ,A_N$, тогда этот факт будет обозначаться так: $A=A_1||A_2||\dots ||A_N$

Используемые функции — обобщённый случай

Здесь описаны функции, с помощью которых можно строить JH-подобные алгоритмы, меняя параметр $d$

S-box — Шаблон:Math

Это функция, преобразующая s-блок (то есть размеры её входного и выходного значений одинаковы и равны 4 битам). В алгоритме используются 2 таких функции: $S_1$ и $S_0$. Их таблицы значений такие:

$x$	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
$S_0(x)$	9	0	4	b	d	c	3	f	1	a	2	6	7	5	8	e
$S_1(x)$	3	c	6	d	5	7	1	9	f	2	0	4	b	a	e	8

Линейное преобразование пар ячеек — Шаблон:Math

Эта функция преобразует пару s-блоков (то есть размеры её входного и выходного значений одинаковы и равны 8 битам). Наиболее лаконичную запись она имеет в терминах конечных полей многочленов.

Рассмотрим конечное поле многочленов над $GF(2)$ степени не выше 3-й. Оно изоморфно полю $GF(2^4)$; установим стандартное для таких случаев соответствие межу полем многочленов и полем чисел: многочлен будет соответствовать числу, равному значению многочлена при $x=2$. Выберем для этого поля многочленов следующий примитивный многочлен:

$x^4+x+1$.

Тогда, если рассматривать $L(A,B)$, как функцию, преобразующую 2 многочлена, а числа и буквы — как многочлены, то

$L(A,B)=((5\bullet A+2\bullet B),(2\bullet A+B))$,

где «$\bullet$» и «$+$» — операции умножения и сложения в данном поле многочленов.

Перемешивание — Шаблон:Math

Функция $P_d$ является композицией трёх более простых перемешиваний, преобразующих массив из $2^d$ битовых векторов (то есть размеры их входных и выходных значений одинаковы и равны $2^d\times k$ битам, где $k$ — число бит в одном элементе этого массива):

$P_d(A)={\varphi }_d(P{\text{'}}_d({\pi }_d(A)))$

Приведем алгоритмы этих перемешиваний, обозначив за $A=A_0||A_1||\dots ||A_{2^d-1}$ и $B=B_0||B_1||\dots ||B_{2^d-1}$ (где $A_i$ и $B_i$ — битовые векторы одинакового размера для всех $i$) — входной и выходной векторы соответственно:

• $B={\pi }_d(A)$:

$fori=0to{2}^{d-2}-1begin$

$B_{4i+0}=A_{4i+0}$

$B_{4i+1}=A_{4i+1}$

$B_{4i+2}=A_{4i+3}$

$B_{4i+3}=A_{4i+2}$

$end$

• $B=P{\text{'}}_d(A)$:

$fori=0to{2}^{d-1}-1begin$

$B_i=A_{2i}$

$B_{i+2^{d-1}}=A_{2i+1}$

$end$

• $B={\varphi }_d(A)$:

$fori=0to{2}^{d-2}-1begin$

$B_{2i}=A_{2i}$

$B_{2i+1}=A_{2i+1}$

$B_{2^{d-1}+2i}=A_{2^{d-1}+2i+1}$

$B_{2^{d-1}+2i+1}=A_{2^{d-1}+2i}$

$end$

Преобразование-раунд — Шаблон:Math

На вход подается $2^{d+2}$- мерный вектор $A$. Выход — $2^{d+2}$- мерный вектор. Так же на вход подается $2^d$-битная константа $C$.

Вектор $A$ представляется в виде массива из $2^d$ полубайт: $A=A_0||A_1||\dots ||A_{2^d-1}$.

Потом над каждым полубайтом $A_i$ производится преобразование $S_0$ или $S_1$ в зависимости от значения $C_i$ (если $C_i=0$, то $S_0$, иначе — $S_1$)

Далее над каждой парой вида $(S_{C_{2i}}(A_{2i}),S_{C_{2i+1}}(A_{2i+1}))$ производится линейное преобразование $L(S_{C_{2i}}(A_{2i}),S_{C_{2i+1}}(A_{2i+1}))$.

И в конце концов результаты опять группируются в вектор, биты которого подвергаются перемешиванию $P_d$.

Это выражается в виде формулы:

$R_d(A,C)=P_d\left(L\right(S_{C_0}(A_0),S_{C_1}(A_1))||L(S_{C_2}(A_2),S_{C_3}(A_3))||\dots ||L(S_{C_{2^d-2}}(A_{2^d-2}),S_{C_{2^d-1}}(A_{2^d-1})\left)\right)$

Преобразование Шаблон:Math

На входе $2^{d+2}$ — мерный вектор $A$. Сначала происходит начальная группировка:

• $B=G_d(A)$:

$fori=0to{2}^{d-1}-1begin$

$B_{8i+0}=A_{i+128\times 0}$

$B_{8i+1}=A_{i+128\times 2}$

$B_{8i+2}=A_{i+128\times 4}$

$B_{8i+3}=A_{i+128\times 6}$

$B_{8i+4}=A_{i+128\times 1}$

$B_{8i+5}=A_{i+128\times 3}$

$B_{8i+6}=A_{i+128\times 5}$

$B_{8i+7}=A_{i+128\times 7}$

$end$

Далее к результату $B$ этой группировки применяется $6\times (d-1)$ преобразований-раундов $R_d(B,C)$ с константами, изменяющимися от раунда к раунду. Начальное значение переменной $C$ задаётся, как целая часть числа $(\sqrt{2}-1)\times 2^{2^d}$, то есть

• $C=\lfloor (\sqrt{2}-1)\times 2^{2^d}\rfloor$:

$fori=1to6\times (d-1)begin$

$C=R_{d-2}(C,0)$

$B=R_d(B,C)$

$end$

Далее происходит конечная разгруппировка, обратная начальной:

• $B_{fin}=G_d^{-1}(B)$,

Где $G_d^{-1}:G_d(G_d^{-1}(B))\equiv B$

Таким образом,

$E_d(A)=G^{-1}(R_d(R_d(R_d(\dots (R_d(G_d(A)),C_1)\dots ),C_{6(d-1)-1}),C_{6(d-1)}))$

$C_i=R_{d-2}(C_{i-1},0),i=1\dots 6(d-1),C_0=\lfloor (\sqrt{2}-1)\times 2^{2^d}\rfloor$

Функция свёртки Шаблон:Math

На входе $2^{d+2}$-битный вектор $H$ и $2^{d+1}$-битный вектор $M$. Сначала $H$ преобразуется путём побитового сложения первой половины этого вектора с $M$, потом над результатом выполняется преобразование $E_d$ и наконец результат преобразуется путём побитового сложения его второй половины с вектором $M$.

Запишем это в виде формул. Пусть $H_{left}$ — первая (старшая) половина вектора $H$, а $H_{right}$ — вторая. Пусть также функции $E_{d-left}(A)$ и $E_{d-right}(A)$ возвращают левую и правую половины $E_d(A)$ соответственно. Тогда

$F_d(H,M)=E_{d-left}((H_{left}\oplus M)||H_{right})||\left(E_{d-right}\right((H_{left}\oplus M)||H_{right})\oplus M)$

Используемые функции — адаптация к аппаратной реализации при d=8

Конкретная реализация во многом зависит от таких параметров, как

1. Желательное быстродействие
2. Желательный размер
3. Желательная технология
4. Желательное энергопотребление
5. Желательная помехоустойчивость
6. Желательная стоимость

Поэтому без задания этих параметров адаптация невозможна. Я дам описание преобразования $L$ с помощью обычных для аппаратной разработки побитовых операций, а также некоторые константы, которые могут пригодиться, если нет существенного ограничения по размерам схемы.

Выражение преобразования Шаблон:Math через простые операции с битами

Пусть $L(A,B)=C_0||C_1||C_2||C_3||D_0||D_1||D_2||D_3,$, тогда

$D_0=B_0\oplus A_1;$

$D_1=B_1\oplus A_2;$

$D_2=B_2\oplus A_3\oplus A_0;$

$D_3=B_3\oplus A_0;$

$C_0=A_0\oplus D_1;$

$C_1=A_1\oplus D_2;$

$C_2=A_2\oplus D_3\oplus D_0;$

$C_3=A_3\oplus D_0.$

где «$\oplus$» — операция «исключающее или».

Пусть входной и выходной векторы lin_trans_in[0:7] и lin_trans_out[0:7] соответственно, тогда

Шаблон:Скрытый

Константы Шаблон:Math при разных Шаблон:Math

Для $l_{hash}=512,384,256,224$ будем иметь соответственно:

Шаблон:Скрытый

Константы Шаблон:Math раундов Шаблон:Math

$C_i=R_6(C_{i-1},0),i=1\dots 42,C_0=\lfloor (\sqrt{2}-1)\times 2^{256}\rfloor$

Представим их в виде массива, $C_{i+1}=$round_const[i][0:255]

Шаблон:Скрытый

Позиции полубайтов после перемешивания Шаблон:Math

Пусть на вход $P_8$ поступил 1024-битный вектор — массив из 256-ти 4-битных векторов: $A=A_1||A_2||\dots ||A_{256}$, а на выходе имеем $B=B_1||B_2||\dots ||B_{256}$, тогда $B_i=A_{permut\mathrm{\_}pose[i*8-1-:8]}$. Это означает, что первый полубайт выходного вектора $B$ будет равен полубайту входного вектора $A$ с номером позиции (от 0 до 255), содержащемся в первом байте константы permut_pose[0:2047], второй полубайт выходного вектора — полубайту входного вектора с номером позиции, содержащемся во втором байте permut_pose[0:2047], и т. д.

Шаблон:Скрытый

Используемые функции — адаптация к программной реализации при d=8

Суть этой адаптации заключается в минимизации числа операций путём использования операций с как можно более длинными операндами. Сделать это позволяют такие технологии, как, например, SIMD, SSE2, AVX.

примеры реализации на языке C

Для пояснения работы функций, а также для того, чтобы показать константы раундов, будут приводиться куски кода на C. Будучи соединёнными в один файл и дополненными функцией main(), приведённой ниже, они компилируются; полученная программа реализует функцию $E_8$.

Шаблон:Скрытый

Шаблон:Скрытый

Функция Шаблон:Math

Преобразует четыре 128-битных вектора в зависимости от 128-битной константы. То есть

$(x_0,x_1,x_2,x_3)=SBox(x_{00},x_{10},x_{20},x_{30},c)$

Алгоритм таков. Введём ещё 128-битную переменную t и проинициализируем переменные начальными значениями

$(x_0,x_1,x_2,x_3)=(x_{00},x_{10},x_{20},x_{30})$,

тогда последовательность присваиваний следующая:

1. $x_3=\mathrm{\neg }{x}_3$
2. $x_0=x_0\oplus (c\mathrm{\&}(\mathrm{\neg }{x}_2))$
3. $t=c\oplus (x_0\mathrm{\&}{x}_1)$
4. $x_0=x_0\oplus (x_2\mathrm{\&}{x}_3)$
5. $x_3=x_3\oplus ((\mathrm{\neg }{x}_1)\mathrm{\&}{x}_2)$
6. $x_1=x_1\oplus (x_0\mathrm{\&}{x}_2)$
7. $x_2=x_2\oplus (x_0\mathrm{\&}(\mathrm{\neg }{x}_3))$
8. $x_0=x_0\oplus (x_1|x_3)$
9. $x_3=x_3\oplus (x_1\mathrm{\&}{x}_2)$
10. $x_1=x_1\oplus (t\mathrm{\&}{x}_0)$
11. $x_2=x_2\oplus t$

Шаблон:Скрытый

Функция Шаблон:Math

Преобразует восемь 128-битных переменных. Пусть $(b_0,b_1,b_2,b_3,b_4,b_5,b_6,b_7)=LinTrans(a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7)$, тогда

$b_4=a_4\oplus a_1$

$b_5=a_5\oplus a_2$

$b_6=a_6\oplus a_3\oplus a_0$

$b_7=a_7\oplus a_0$

$b_0=a_0\oplus b_5$

$b_1=a_1\oplus b_6$

$b_2=a_2\oplus b_7\oplus b_4$

$b_3=a_3\oplus b_4$

Шаблон:Скрытый

Функция Шаблон:Math

Преобразует 128-битную переменную в зависимости от целой константы $n:6\ge n\ge 0$. Эта функция не оптимизируется для использования 128-битных переменных, однако для совместного использования с другими функциями из этого раздела она необходима.

Пусть $b=Permutation(a,n)$, $b=b_0||b_1||\dots ||b_{127},a=a_0||a_1||\dots ||a_{127}$ где. Алгоритм получения числа $b$ таков:

• $b=a$:

$fori=0to\frac{128}{2\times 2^n}-1begin$

$Swap((b_{2\times 2^n\times i+0}||b_{2\times 2^n\times i+1}||\dots ||b_{2\times 2^n\times i+2^n-1}),(b_{2\times 2^n\times i+2^n+0}||b_{2\times 2^n\times i+2^n+1}||\dots ||b_{2\times 2^n\times i+2^n+2^n-1}))$

$end$

Здесь запись $Swap(p,q)$ означает такой участок алгоритма, после которого переменная $p$ принимает значение, которое было у переменной $q$, а переменная $q$ принимает значение, которое было у переменной $p$.

Шаблон:Скрытый

Функция Шаблон:Math, адаптированная к программной реализации

Преобразует 1024-битный вектор. Совпадает с функцией $E_8$, описанной в обобщённом случае (в том смысле, что при совпадении значений аргументов совпадают значения функций). Пусть на вход поступил 1024-битный вектор. Представим его в виде набора 8-ми 128-битных переменных: $(x_0,x_1,x_2,x_3,x_4,x_5,x_6,x_7)$. После следующих преобразований они будут представлять собой выходной вектор:

$forr=0to41begin$

$(x_0,x_2,x_4,x_6)=SBox(x_0,x_2,x_4,x_6,C_r^{even})$

$(x_1,x_3,x_5,x_7)=SBox(x_1,x_3,x_5,x_7,C_r^{odd})$

$(x_0,x_2,x_4,x{6}_{,}{x}_1,x_3,x_5,x_7)=LinTrans(x_0,x_2,x_4,x_6,x_1,x_3,x_5,x_7)$

$x_1=Permutation(x_1,rmod7)$

$x_3=Permutation(x_3,rmod7)$

$x_5=Permutation(x_5,rmod7)$

$x_7=Permutation(x_7,rmod7)$

$end$

Использующиеся 128-битные константы задаются следующим образом: $C_r^{odd}=C_r^1||C_r^3||\dots ||C_r^{255},C_r^{even}=C_r^0||C_r^2||\dots ||C_r^{254},C_r=R_6(C_{r-1},0),r=1\dots 42,C_0=\lfloor (\sqrt{2}-1)\times 2^{256}\rfloor$

Шаблон:Скрытый

Исходные данные

Входной параметр

$l_{hash}$ — длина хэша (число бит в выходном векторе хеш-функции).

Может принимать только следующие значения:

• 224, 256, 384 и 512;

напомним, что данная статья, строго говоря, описывает семейство из 4-х хеш-функций.

Входное сообщение

Представляет собой число — длину сообщения $L$ и битовый вектор $M_0$ (если $L\ne 0$). Даже если $L=0$ никаких трудностей для вычисления $JH(M_0)$ не возникает.

Алгоритм вычисления Шаблон:Math

1) Дополнение входного вектора

Присоединение к сообщению $M_0$ дополнительных бит в конце. Происходит в три этапа:

1.1)Дополнение единицей.

Присоединение к концу сообщения единичного бита.

1.2)Дополнение нулями.

Присоединение к концу сообщения, дополненного единицей, нулевых бит в количестве $383+(-Lmod512)$ штук.

1.3)Дополнение длиной сообщения.

Присоединение к концу сообщения, дополненного единицей и нулями, 128 бит, в которых записана длина исходного сообщения (например, если $L=2$, то добавка будет выглядеть так: $0\dots 010$).

В итоге получится дополненное сообщение $M$ с длиной, кратной $512$.

2) Свёртка дополненного входного вектора функцией $F_8$

$M$ разбивается на блоки по $512$ бит. Обозначим за $N$ число таких блоков.

Свёртка происходит за $N$ итераций. На $i$-той итерации на вход $F_8$ поступает $i$-й $512$-битный блок $M_i$ сообщения $M$ и значение $H_{i-1}=F_8(H_{i-2},M_{i-1})$, вычисленное на предыдущей итерации. Имеется также нулевая итерация, на которой вычисляется $H_0$ из $H_{-1}$ и $M_0$. Таким образом имеем:

$H=H_N=F_8(H_{N-1},M_N)=F_8(F_8(H_{N-2},M_{N-1}),M_N)=\dots =F_8(\dots (H_{-1},M_0)\dots )$.

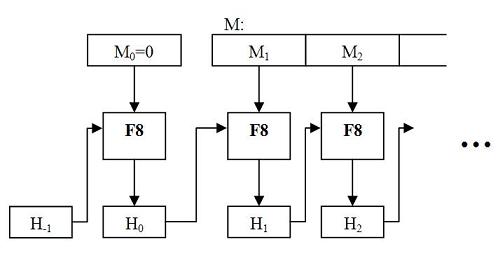
$H_{-1}$ и $M_0$ выбираются так: первые $16$ бит $H_{-1}$ равны входному параметру $l_{hash}$ — размеру выходного хэша (для $l_{hash}$, равных $512,324,256$ или $224$ это соответственно 0200h, 0180h, 0100h или 00e0h), а остальные биты $H_{-1}$ и все биты $M_0$ задаются равными $0$.

3) Выборка хэша из выхода функции $F_8$

Из $1024$-битного вектора $H_N=H_N^0||H_N^1||\dots ||H_N^{1023}$, полученного на выходе $F_8$ на последней итерации свёртки дополненного входного сообщения, выбираются последние $l_{hash}$ бит:

$JH(M_0)=H_N^{1023+1-l_{hash}}||H_N^{1023+2-l_{hash}}||\dots ||H_N^{1023}$

См. также

• Шаблон:Iw
• Advanced Encryption Standard
• SP-сеть

Ссылки

• документация, актуальная в ноябре 2011 года
  • http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_round3.pdf Шаблон:Wayback
• варианты исходных кодов на VHDL моделей электронных устройств, реализующих JH:
  • http://cryptography.gmu.edu/athena/sources/2011_10_01/folded_unrolled/JH_fv2.zip
  • http://cryptography.gmu.edu/athena/sources/2011_10_01/folded_unrolled/JH_u2.zip
  • http://cryptography.gmu.edu/athena/sources/2011_10_01/basic/JH_basic.zip
• варианты исходных кодов на C, реализующих JH:
  • http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_ref.h Шаблон:Wayback
  • http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_bitslice_ref64.h Шаблон:Wayback
  • http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_sse2_opt64.h Шаблон:Wayback
• страница автора для поддержки JH
  • http://www3.ntu.edu.sg/home/wuhj/research/jh/index.html Шаблон:Wayback
• ссылки на исследования криптоаналитиков и архивы файлов, отправлявшиеся на конкурс SHA-3
  • http://ehash.iaik.tugraz.at/wiki/JH
• ссылки на архивы с исходными кодами на VHDL (и сопутствующими файлами) моделей электронных устройств, реализующих алгоритмы хеш-функций, прошедших во второй тур SHA-3
  • http://cryptography.gmu.edu/athena/index.php?id=source_codes
• ссылки на исследования характеристик электронных устройств (реализованных на ПЛИС), реализующих алгоритмы хеш-функций, прошедших в финал второго тура SHA-3
  • http://ehash.iaik.tugraz.at/wiki/SHA-3_Hardware_Implementations
  • https://web.archive.org/web/20120628192806/http://rijndael.ece.vt.edu/sha3/publications.html