Задача о паре ближайших точек

Пара ближайших точек выделена красным цветом

Задача о паре ближайших точек — это задача вычислительной геометрии. Дано n точек в метрическом пространстве, нужно найти пару точек с наименьшим расстоянием между ними.

Задача о ближайших точках на евклидовой плоскостиШаблон:Sfn была одной из первых геометрических задач, которая подверглась систематическому изучению со стороны вычислительной сложности геометрических алгоритмов.

Наивный алгоритм нахождения расстояний между всеми парами в пространстве размерности d и выбора среди них наименьшего требует времени Шаблон:Nowrap. Оказывается, что задача может быть решена за время $O(n\log n)$ в евклидовом пространстве или L^p пространстве фиксированной размерности dШаблон:Sfn. В модели вычислений Шаблон:Не переведено 5 алгоритм со временем Шаблон:Nowrap оптимален при сведении от Шаблон:Не переведено 5. В вычислительной модели, в которой принимается, что Шаблон:Не переведено 5 вычисляема за постоянное время, задача может быть решена за время $O(n\log \log n)$Шаблон:Sfn. Если мы позволяем применение рандомизации вместе с функцией floor, задача может быть решена за время Шаблон:NowrapШаблон:SfnШаблон:R.

Алгоритм полного перебора

Пара ближайших точек может быть вычислена за время O(n²) путём выполнения полного перебора. Чтобы это сделать, можно вычислить расстояние между всеми Шаблон:Nowrap парами точек, затем выбрать пару с наименьшим расстоянием, как показано ниже.

minDist = infinity
for i = 1 to length(P) - 1
 for j = i + 1 to length(P)
  let p = P[i], q = P[j]
  if dist(p, q) < minDist:
   minDist = dist(p, q)
   closestPair = (p, q)
return closestPair

Планарный случай

Задача может быть решена за время $O(n\log n)$ с помощью рекурсивного подхода «разделяй и властвуй», например, такШаблон:Sfn:

1. Сортируем точки согласно их x-координатам;
2. Разбиваем множество точек на два подмножества равного размера вертикальной прямой $x=x_{mid}$;
3. Решаем задачу рекурсивно на левой и на правой частях. Это приводит к левому минимальному расстоянию $d_{Lmin}$ и правому минимальному расстоянию $d_{Rmin}$, соответственно;
4. Находим минимальное расстояние $d_{LRmin}$ среди пар точек, из которых одна точка лежит слева от вертикальной линии, а другая точка лежит справа от прямой;
5. Конечным ответом будет минимальное значение среди $d_{Lmin}$, $d_{Rmin}$ и $d_{LRmin}$.

Разделяй и властвуй: наблюдение разреженных прямоугольников

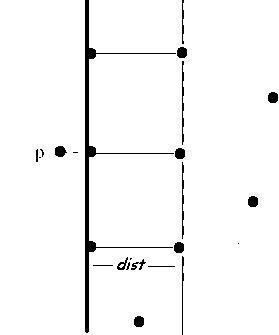
Оказывается, что шаг 4 может быть выполнен за линейное время. Снова, наивный подход потребовал бы вычисление расстояний для всех пар слева/справа, то есть квадратичное время. Ключевое наблюдение основывается на следующем свойстве разреженности множества точек. Мы уже знаем, что пара ближайших точек не находятся на большем расстоянии, чем $\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}=\min (d_{Lmin},d_{Rmin})$. Поэтому, для каждой точки Шаблон:Math слева от разделяющей прямой мы должны сравнить расстояния до точек, которые лежат в прямоугольнике с размерами Шаблон:Math как показано на рисунке. И этот прямоугольник может содержать не более шести точек, попарное расстояние между которыми не менее $d_{Rmin}$. Таким образом, достаточно вычислить на 4-м шаге Шаблон:Math расстоянийШаблон:Sfn. Рекуррентное отношение для числа шагов может быть записано как $T(n)=2T(\frac{n}{2})+O(n)$, которое может быть решено с помощью основной теоремы для рекурренции разделяй и властвуй, что даёт $O(n\log n)$.

Так как пара ближайших точек определяют ребро в триангуляции Делоне и соответствуют двум смежным ячейкам в диаграмме Вороного, пара ближайших точек может быть определена за линейное время, если дана одна из этих двух структур. Вычисление триангуляции Делоне или диаграммы Вороного занимает время $O(n\log n)$. Эти подходы не эффективны для размерностей Шаблон:Math, в то время как алгоритм «разделяй и властвуй» может быть обобщён до времени выполнения $O(n\log n)$ для любого постоянного значения размерности Шаблон:Math.

Динамическая задача ближайшей пары

Шаблон:Не переведено 5 для задачи пары ближайших точек ставится следующим образом:

• Если дано динамическое множество объектов, найти алгоритмы и структуры данных для эффективного перевычисления пары ближайших точек каждый раз, когда объект вставляется или удаляется.

Если ограничивающий прямоугольник для всех точек заранее известен и доступна функция floor с постоянным временем работы, то была предложена структура данных с ожидаемой памятью O(n), которая поддерживает ожидаемое время (среднее время) вставки и удаления O(log n) и постоянное время запроса. Если задача модифицирована для модели алгебраического дерева принятия решения, вставки и удаления потребуют среднее время $O({\log }^{2}n)$Шаблон:Sfn. Следует отметить, что сложность указанной выше динамической задачи о паре ближайших точек экспоненциально зависит от размерности d, поэтому алгоритм становится менее пригодным для задач высокой размерности.

Алгоритм для динамической задачи пары ближайших точек в пространстве размерности d разработал Сергей Беспамятных в 1998 годуШаблон:Sfn. Точки могут быть вставлены и удалены за время O(logn) на одну точку (в худшем случае).

См. также

• Геоинформационная система
• Задача поиска ближайшего соседа
• Задача о покрытии множества

Литература

• Шаблон:Книга
  • Перевод: Шаблон:Книга
• Шаблон:Книга
  • Перевод: Шаблон:Книга
• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Статья Предварительная версия была доложена на симпозиуме «4th Annu. ACM-SIAM Symp. on Discrete Algorithms», 1993, стр. 301—310
• Шаблон:Статья
• UCSB Lecture Notes
• rosettacode.org — Closest pair of points implemented in multiple programming languages
• Line sweep algorithm for the closest pair problem