Интегральный логарифм
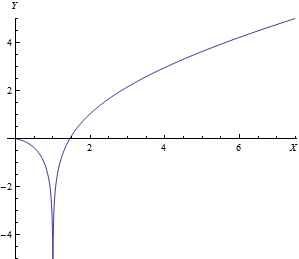
Интегральный логарифм — специальная функция, определяемая интегралом
Для устранения сингулярности при иногда применяется сдвинутый интегральный логарифм:
Эти две функции связаны соотношением:
Интегральный логарифм введён Леонардом Эйлером в 1768 году.
Интегральный логарифм и интегральная показательная функция связаны соотношением:
Интегральный логарифм имеет единственный положительный ноль в точке (число Рамануджана — Солднера).
Разложение в ряд
Из тождества, связывающего и следует ряд:
где — постоянная Эйлера — Маскерони.
Быстрее сходится ряд, выведенный Сринивасой Рамануджаном:
Интегральный логарифм и распределение простых чисел
Интегральный логарифм играет важную роль в исследовании распределения простых чисел. Он представляет собой более точное приближение к числу простых чисел, не превосходящих заданного числа, чем . При справедливости гипотезы Римана выполняется[1]
Для не слишком больших , однако доказано, что при некотором достаточно большом неравенство меняет знак. Это число называется числом Скьюза, в настоящее время известно, что оно заключено где-то между 1019[2] и 1,3971672·10316 ≈ e727,951336108[3].
Примечания
Литература
- Математический энциклопедический словарь. — Шаблон:М., 1995. — с. 238.
- ↑ Совр. пробл. матем., 2008, выпуск 11. - с. 30-31
- ↑ Шаблон:Публикация Доказательство использует гипотезу Римана.
- ↑ Шаблон:Публикация Шаблон:MR. Указанная оценка не требует гипотезы Римана.