Изобарный процесс
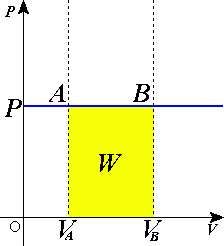

Изобари́ческий — термодинамический изопроцесс, происходящий в физической системе при постоянном внешнем давлении[1].
Согласно закону Гей-Люссака, в идеальном газе при изобарном процессе отношение объёма к температуре постоянно: .
Если использовать уравнение Клапейрона — Менделеева, то работа, совершаемая газом при расширении или сжатии газа, равна
Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии:
Теплоёмкость
Молярная теплоёмкость при постоянном давлении обозначается как В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера
Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной Шаблон:Math:
- для одноатомных газов , то есть около 20,8 Дж/(моль·К);
- для двухатомных газов , то есть около 29,1 Дж/(моль·К);
- для многоатомных газов , то есть около 33,2 Дж/(моль·К).
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).
Изменение энтропии
Изменение энтропии при квазистатическом изобарном процессе равно В случае, если изобарный процесс происходит в идеальном газе, то следовательно, изменение энтропии можно выразить как Если пренебречь зависимостью от температуры (это предположение справедливо, например, для идеального одноатомного газа, но в общем случае не выполняется), то