Большой ромбогексаэдр
| Большой ромбогексаэдр | |
|---|---|

| |
| Тип | Однородный звёздчатый многогранник |
| Элементы | F = 18, E = 48, V = 24 |
| Характеристика Эйлера |
= -6 |
| Грани по числу сторон |
12{4} + 6{8/3}} |
| Символ Витхоффа | 2 4/3 (3/24/2) | |
| Группа симметрии | Oh, [4,3], (*432) |
| Обозначения | U21, C82, W103 |
| Двойственный | Большой ромбогексаэдр |
| Вершинная фигура |  4.8/3.4/3.8/5 |
Большой ромбогексаэдр — невыпуклый однородный многогранник. Двойственным ему является большой ромбогексакрон[1]. Вершинная фигура — самопересекающийся четырёхугольник.
Ортогональные проекции
Раскраска
Есть споры по поводу раскраски граней этого многогранника. Хотя обычным способом раскраски многоугольников является раскраска в один цвет всей внутренности многоугольника, это может привести к появлению областей, висящих как пластинки над пустым пространством. В результате иногда используется «неораскраска». В неораскраске ориентируемые многогранники раскрашиваются традиционно, а грани неориентируемых многогранников раскрашиваются по модулю 2 (только области нечётной Шаблон:Не переведено 5)[2].
 Традиционная раскраска |
 «Неораскраска» |
Связанные многогранники
Многогранник имеет то же Шаблон:Не переведено 5, что и у выпуклого усечённого куба. Кроме того, он имеет то же Шаблон:Не переведено 5, что и у Шаблон:Не переведено 5 (12 таких же квадратных граней), и у Шаблон:Не переведено 5 (одинаковые восьмиугольные грани).
 Усечённый куб |
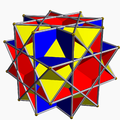 Шаблон:Не переведено 5 |
 Шаблон:Не переведено 5 |
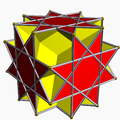 Большой ромбогексаэдр |
Многогранник может быть получен как исключающее «ИЛИ» трёх Шаблон:Не переведено 5.
Большой ромбогексакрон
| Большой ромбогексакрон | |
|---|---|

| |
| Тип | Звёздчатый многогранник |
| Элементы | F = 24, E = 48, V = 18 |
| Характеристика Эйлера |
= -6 |
| Грань | 
|
| Группа симметрии | Oh, [4,3], (*432) |
| Обозначения | DU21 |
| Двойственный | Большой ромбогексаэдр |
Большой ромбогексакрон — невыпуклый изоэдральный многогранник. Многогранник является двойственным большому ромбогексаэдру (U21)[3]. Многогранник имеет 24 одинаковые грани в форме галстука-бабочки, 18 вершин и 48 рёбер[4]
Многогранник имеет 12 внешних вершин, которые имеют одно и то же Шаблон:Не переведено 5, как у кубооктаэдра, и 6 внутренних вершин с расположением вершин как у октаэдра.
По геометрии поверхности многогранник можно рассматривать как тело, визуально подобное каталанову телу, гекзакисоктаэдру, в котором более тонкие пирамиды с ромбами в основании присоединены к каждой грани ромбододекаэдра.
Примечания
Литература
Ссылки
- ↑ Шаблон:Cite web
- ↑ Шаблон:Cite web
- ↑ Шаблон:Mathworld
- ↑ Great Rhombihexacron Шаблон:Wayback—Bulatov Abstract Creations
