Кривая Безье

Кривы́е Безье́ — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

Кривая Безье является частным случаем многочленов Бернштейна, описанных русским математиком Сергеем Натановичем Бернштейном в 1912 году.

Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.

Определение

Пусть в пространстве ${ℝ}^m$ размерности $m⩾1$ над $ℝ$ задана последовательность контрольных точек $({𝐏}_0,\dots ,{𝐏}_n)$, где $n⩾0$, а ${𝐏}_k=(x_{1,k},\dots ,x_{m,k})$ для $k=0,\dots ,n$.

Тогда множество $\{𝐁(t)|0⩽t⩽1\}$ точек $𝐁(t)=(z_1(t),\dots ,z_m(t))$ с координатами $(z_j(t){)}_{j=1,\dots ,m}$, параметрически задаваемыми выражениями

$z_j(t)=\sum _{k=0}^n{x}_{j,k}{b}_{k,n}(t)$ для $0⩽t⩽1,$ где $j=1,\dots ,m,$ а $b_{k,n}(t)=(\genfrac{}{}{0ex}{}{n}{k})t^k(1-t{)}^{n-k}$ для $k=0,\dots ,n$,

называется кривой Безье.

Многочлен $b_{k,n}(t)$ степени $n$ по параметру $t$ называется базисной функцией (соответствующей контрольной точке ${𝐏}_k$) кривой Безье или полиномом Бернштейна.

Здесь $(\genfrac{}{}{0ex}{}{n}{k})=\frac{n!}{k!(n-k)!}$ — число сочетаний из $n$ по $k$.

Замечания

1. Кривая Безье, соответствующая как $({𝐏}_0)$ так и $({𝐏}_0,{𝐏}_0,\dots ,{𝐏}_0)$, есть точка ${𝐏}_0$.
2. Кривая Безье, соответствующая паре $({𝐏}_0,{𝐏}_1)$, то есть при $n=1$, есть (линейно) параметризованный отрезок, соединяющий точку ${𝐏}_0$ (при $t=0$) с точкой ${𝐏}_1$ (при $t=1$).
3. При любом порядке $n⩾0$ кривая Безье содержит как точку ${𝐏}_0$ (это — образ параметра $t=0$), так и точку ${𝐏}_n$ (это — образ параметра $t=1$).
4. Кривая Безье (в общем случае, то есть если не выродилась в точку ${𝐏}_0$) ориентируема, поскольку является образом ориентированного отрезка $[0;1]$. Последовательностям контрольных точек $({𝐏}_0,{𝐏}_1,\dots ,{𝐏}_{n-1},{𝐏}_n)$ и $({𝐏}_n,{𝐏}_{n-1},\dots ,{𝐏}_1,{𝐏}_0)$ соответствуют кривые Безье, которые совпадают как множества точек, но имеют (в общем случае) противоположные ориентации.
5. Кривые Безье, соответствующие последовательностям контрольных точек $({𝐏}_0,{𝐏}_1,{𝐏}_2)$ и $({𝐏}_0,{𝐏}_2,{𝐏}_1)$, при ${𝐏}_1\ne {𝐏}_2$ не совпадают.
6. Если изменить $(x_{j,0},\dots ,x_{j,n})$, то изменяется только $z_j(t)$.

Виды кривых Безье

Линейные кривые

Файл:TrueType 1 Line.PNG

Линейная кривая Безье

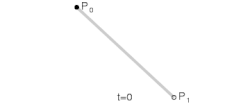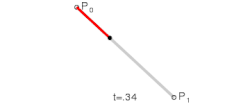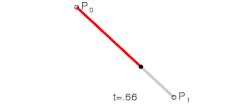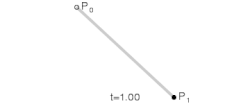
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P₀ и P₁ определяют его начало и конец. Кривая задаётся уравнением:

$𝐁(t)=(1-t){𝐏}_0+t{𝐏}_{1}t\in [0,1]$.

Квадратичные кривые

Файл:TrueType 2 Arc.PNG

Квадратичная кривая Безье

Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: P₀, P₁ и P₂.

$𝐁(t)=(1-t{)}^2{𝐏}_0+2t(1-t){𝐏}_1+t^2{𝐏}_2,t\in [0,1]$.

Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF-файлах.

$t=\frac{{𝐏}_0-{𝐏}_1\pm \sqrt{({𝐏}_0-2{𝐏}_1+{𝐏}_2)𝐁+{𝐏}_1^2-{𝐏}_0{𝐏}_2}}{{𝐏}_0-2{𝐏}_1+{𝐏}_2},{𝐏}_0-2{𝐏}_1+{𝐏}_2\ne 0$

$t=\frac{𝐁-{𝐏}_0}{2({𝐏}_1-{𝐏}_0)},{𝐏}_0-2{𝐏}_1+{𝐏}_2=0,{𝐏}_0\ne {𝐏}_1$

$t=\sqrt{\frac{𝐁-{𝐏}_0}{{𝐏}_2-{𝐏}_1}},{𝐏}_0={𝐏}_1\ne {𝐏}_2$

Кубические кривые

Кубическая кривая Безье

В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

$𝐁(t)=(1-t{)}^3{𝐏}_0+3t(1-t{)}^2{𝐏}_1+3t^2(1-t){𝐏}_2+t^3{𝐏}_3,t\in [0,1]$.

Четыре опорные точки P₀, P₁, P₂ и P₃, заданные в 2- или 3-мерном пространстве, определяют форму кривой.

Линия берёт начало из точки P₀, направляясь к P₁ и заканчивается в точке P₃, подходя к ней со стороны P₂. То есть, кривая не проходит через точки P₁ и P₂, они используются для указания её направления. Длина отрезка между P₀ и P₁ определяет, как скоро кривая повернёт к P₃.

В матричной форме кубическая кривая Безье записывается следующим образом:

$𝐁(t)=\left[\begin{array}{cccc}{t}^3& t^2& t& 1\end{array}\right]{𝐌}_B\left[\begin{array}{c}{𝐏}_0\\ {𝐏}_1\\ {𝐏}_2\\ {𝐏}_3\end{array}\right]$,

где ${𝐌}_B$ называется базисной матрицей Безье:

${𝐌}_B=\left[\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 3& 0\\ -3& 3& 0& 0\\ 1& 0& 0& 0\end{array}\right]$

В современных графических системах и форматах, таких как PostScript (а также основанных на нём форматах Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG), Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P₀ до P₁ находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P₀ и P₁. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P₀ и P₁.

Квадратичные кривые

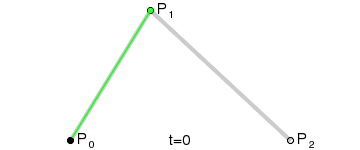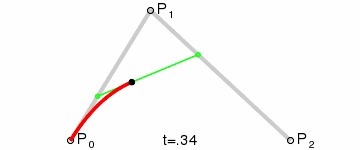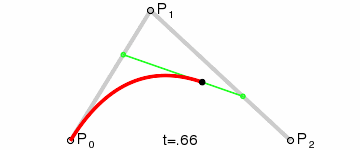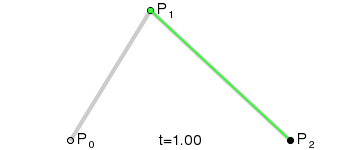
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q₀ и Q₁ из условия, чтобы параметр t изменялся от 0 до 1:

• Точка Q₀ изменяется от P₀ до P₁ и описывает линейную кривую Безье.
• Точка Q₁ изменяется от P₁ до P₂ и также описывает линейную кривую Безье.
• Точка B изменяется от Q₀ до Q₁ и описывает квадратичную кривую Безье.

Построение квадратичной кривой Безье

Анимация t: [0;1]

Кривые высших степеней

Для построения кривых высших порядков соответственно требуется больше промежуточных точек. Для кубической кривой это промежуточные точки Q₀, Q₁ и Q₂, описывающие линейные кривые, а также точки R₀ и R₁, которые описывают квадратичные кривые: более простое уравнение $\frac{P_0{Q}_0}{P_0{P}_1}=\frac{Q_1{P}_1}{P_1{P}_2}=\frac{B{R}_0}{R_1{R}_0}$.

Построение кубической кривой Безье

Анимация t: [0;1]

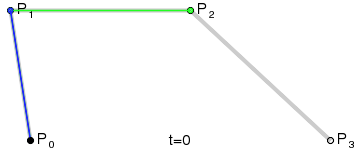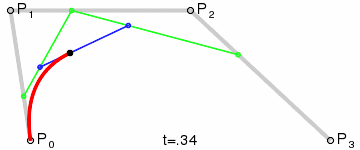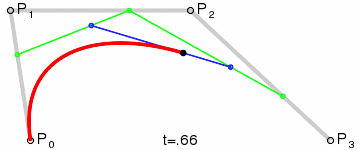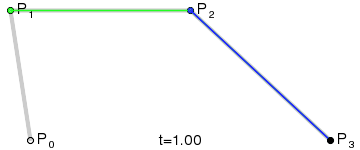Для кривых четвёртой степени это будут точки Q₀, Q₁, Q₂ и Q₃, описывающие линейные кривые, R₀, R₁ и R₂, которые описывают квадратичные кривые, а также точки S₀ и S₁, описывающие кубические кривые Безье:

Построение кривой Безье 4-й степени

Анимация t: [0;1]

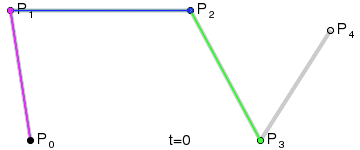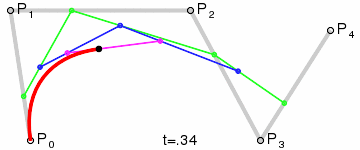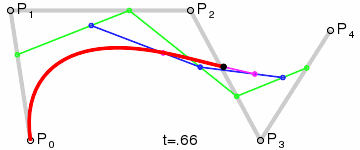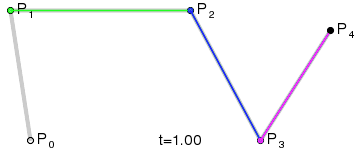Свойства кривой Безье

• непрерывность заполнения сегмента между начальной и конечной точками;
• кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
• при наличии только двух контрольных точек сегмент представляет собой прямую линию;
• прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
• кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
• масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, поскольку с математической точки зрения она «аффинно инвариантна»;
• изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
• любой частичный отрезок кривой Безье также является кривой Безье;
• степень (порядок) кривой всегда на одну ступень меньше числа контрольных точек. Например, при трёх контрольных точках форма кривой — парабола, так как парабола — кривая 2-го порядка;
• окружность не может быть описана параметрическим уравнением кривой Безье;
• невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые), хотя существуют алгоритмы, строящие приближённую параллельную кривую Безье с приемлемой для практики точностью.

Применение в компьютерной графике

Шаблон:Main Благодаря простоте задания и манипуляции кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того, аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики, например Adobe Illustrator или Inkscape, подобные фрагменты известны под названием «путей» (path), а в 3DS Max и подобных программах 3D-моделирования кривые Безье имеют название «сплайны».

Преобразование квадратичных кривых Безье в кубические

Квадратичная кривая Безье с координатами $(x_0;y_0),(x_1;y_1),(x_2;y_2)$ преобразовывается в кубическую кривую Безье с координатами $(x_0;y_0),(x_0+\frac{2\cdot (x_1-x_0)}{3};y_0+\frac{2\cdot (y_1-y_0)}{3}),(x_1+\frac{x_2-x_1}{3};y_1+\frac{y_2-y_1}{3}),(x_2;y_2)$.

Уровень дискретизации Кривых Безье

Уровень дискретизации определяется следующим образом:

$|B_{next}-B_{prev}|=1$

, то есть каждая следующая точка должна отличаться от предыдущей на 1 (допустим пиксель). Причём, если задать $B$ следующим образом:

$|\sum _{k=0}^n\frac{n!}{k!\times (n-k)!}\times t_{next}^k\times (1-t_{next}{)}^{n-k}\times P_k-\sum _{k=0}^n\frac{n!}{k!\times (n-k)!}\times t_{prev}^k\times (1-t_{prev}{)}^{n-k}\times P_k|=1$

Через него можно вычислить $\mathrm{\Delta }t$.

Решим это уравнение для кривых Безье первого порядка (линейных):

$B(t)=(1-t)\times P_0+t\times P_1,0\le t\le 1$

$B(t)=\{\begin{array}{c}x=(1-t)\times P_{0_x}+t\times P_{1_x}\\ y=(1-t)\times P_{0_y}+t\times P_{1_y}\end{array}$

Запишем разницу точек для одной оси:

$|P_0-t_{next}\times P_0+t_{next}\times P_1-P_0+t_{prev}\times P_0-t_{prev}\times P_1|=1$

Вынесем общие множители за скобки:

$|t_{next}\times (P_0-P_1)-t_{prev}\times (P_0-P_1)|=1$

Найдём $\mathrm{\Delta }t$:

$\mathrm{\Delta }t=|t_{next}-t_{prev}|=\left|\frac{1}{P_0-P_1}\right|$

так можно вычислить уровень дискретизации для обхода конкретной оси кривой Безье определённого порядка. То есть Вам нужно получить 16 таких уравнений для кривых Безье с 1го по 16 порядок, она всегда задаётся точками, их координаты достаточно будет подставить в полученное уравнение, чтобы обойти кривую с минимальным однозначным уровнем дискретизации.

См. также

• Поверхность Безье
• NURBS
• B-сплайн
• Кривые

Литература

• Шаблон:Книга

Ссылки

• Wolfram Math World Bézier CurveШаблон:Ref-en
• American Mathematical Society From Bézier to BernsteinШаблон:Ref-en
• Кривые Безье в компьютерных играх [1]Шаблон:Ref-ru
• Часы на кривых БезьеШаблон:Ref-ru
• A Primer on Bézier Curves