Параллельные прямые

Линейка для черчения параллельных прямых

Паралле́льные прямы́е (от Шаблон:Lang-grc буквально «идущий рядом; идущий вдоль другого») в планиметрии — непересекающиеся прямые. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.

Параллельность прямых $m$ и $n$ принято обозначать следующим образом: $m\parallel n.$

В евклидовой геометрии

На чертежах параллельные линии выделяются одинаково направленными стрелками.

В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются.

В другом варианте определения совпадающие прямые также считаются параллельными. Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности.

Свойства

• Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Замена пятого постулата контр-утверждением ведёт к геометрии Лобачевского (см. ниже) или к геометрии Римана (в зависимости от того, какое утверждение выбрано: можно провести больше одной прямой или ни одной).
• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
  • Соответственные углы — пара углов, расположенных в одной полуплоскости относительно секущей, вершина которых есть точки пересечения каждой из параллельных прямых с секущей, стороны углов лежат на соответствующей прямой и на секущей, причём только одна из них относительно «своей» прямой лежит по разные от этой прямой они равны (Рис.1).
  • Накрест лежащие углы — пара углов с вершинами в точках пересечения каждой из параллельных прямых с секущей и расположены по разные стороны от неё, причём стороны углов принадлежат параллельным прямым и секущей. Накрест лежащие углы равны (Рис.2).
  • Внутренние односторонние углы в сумме составляют 180° (Рис.3).

Рис.1: Соответственные углы равны, $\alpha ={\alpha }_1$.	Рис.2: Внутренние накрест лежащие углы равны, $\alpha ={\gamma }_1$.	Рис.3: Односторонние углы являются дополнительными, $\alpha +{\delta }_1=180^{\circ }$.

• Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
• Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.

Построение параллельных прямых

Построение двух параллельных прямых на плоскости с помощью циркуля и линейки можно разделить на несколько этапов:

1. Построение прямой $a$, относительно которой нужно построить параллельную прямую.
2. Построение прямой $b$, перпендикулярной прямой $a$ (см. построение перпендикуляра).
3. Построение прямой $c$, перпендикулярной прямой b, и не совпадающей с прямой $a$ (аналогично построению прямой $b$).

В стереометрии

В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися прямыми.

В геометрии Лобачевского

Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к ней

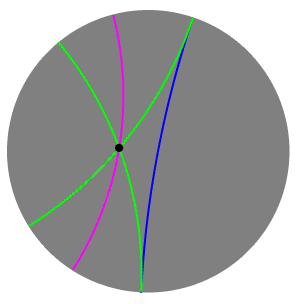
В геометрии Лобачевского в плоскости через точку $C$ вне данной прямой $AB$ проходит бесконечное множество прямых, не пересекающих $AB$. Прямая $CE$ называется равнобежной прямой $AB$ в направлении от $A$ к $B$, если:

1. точки $B$ и $E$ лежат по одну сторону от прямой $AC$;
2. прямая $CE$ не пересекает прямую $AB$, но всякий луч, проходящий внутри угла $ACE$, пересекает луч $AB$.

Аналогично определяется прямая, равнобежная $AB$ в направлении от $B$ к $A$.

Равнобежные прямые называются также асимптотически параллельными или просто параллельными. Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.

Свойства

• Расходящиеся параллельные прямые имеют единственный общий перпендикуляр.
  • Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.

• Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.

См. также

• Параллельность плоскостей
• Антипараллельные прямые
• Перпендикулярность
• Ортогональность