Стирающий код

Стирающий код (Шаблон:Lang-en) — в теории кодирования помехоустойчивый код, способный восстановить целые пакеты данных в случае их потери. Такой код позволяет бороться с утечками данных при передаче по каналам связи или работе с памятью. Обычно он используется, когда точная позиция потерянных данных известна априори.

Графическое представление процессов кодирования и декодирования

Принцип работы

Стирающий код преобразует сообщение из $k$ символов в более длинное сообщение (кодовое слово) из $n$ символов так, что исходное сообщение может быть восстановлено по $k^{\prime }$ любым символам. Такой код называется $(n,k)$ кодом, выражение $r=k/n$ — кодовой долей, выражение $k^{\prime }/k$ — эффективностью приёма.

Стирающий код обычно используется на верхних уровнях стека протоколов каналов передачи и хранения информации.

Оптимальный стирающий код

Оптимальный стирающий отличается тем, что любых $k$ из $n$ символов кодового слова достаточно для восстановления исходного сообщения, то есть они имеют оптимальную эффективность приёма.

Проверка чётности

Рассмотрим случай, когда $n=k+1$. С помощью набора из $k$ значений $\{v_i{\}}_{1\le i\le k}$ вычисляется контрольная сумма и добавляется к $k$ исходным значениям:

$v_{k+1}=-\sum _{i=1}^k{v}_i$.

Теперь в набор $\{v_i{\}}_{1\le i\le k+1}$ из $k+1$ значений включена контрольную сумму. В случае потери одного из значений $v_e$, его можно будет с лёгкостью восстановить с помощью суммирования оставшихся:

$v_e=-\sum _{i=1,i\ne e}^{k+1}{v}_i$.

Более сложные комбинации искомых и получаемых значений представляют собой Граф Таннера.

Линейный код

Важным подклассом стирающего кода является линейный код. Его название связано с тем, что он может быть проанализирован с помощью линейной алгебры. Пусть $x=x_0\dots x_{k-1}$ — исходные данные, $G$ — матрица размера $n\times k$, тогда закодированные данные $(n,k)$- кода могут быть представлены как $\overrightarrow{y}=G\overrightarrow{x}$. Предположим, что приёмник получил $k$ компонент вектора $\overrightarrow{y}$, тогда исходные данные могут быть восстановлены с помощью $k$ уравнений, связанных с известными компонентами вектора $\overrightarrow{y}$. Пусть матрица $G^{\prime }$ размера $k\times k$ соответствует этой системе уравнений. Восстановление возможно, если все эти уравнения линейно независимые и, в общем случае, это означает, что любая матрица размера $k\times k$ обратима. Матрица $G$ называется генерирующей матрицей кода, так как любой допустимый $\overrightarrow{y}$ может быть получен как линейная комбинация столбцов матрицы $G$. Так как её ранг равен $k$, то любое подмножество из $k$ закодированных элементов должно содержать информацию о всех $k$ исходных данных. Для получения исходных данных необходимо решить линейную систему: $\overrightarrow{y^{\prime }}=G^{\prime }\overrightarrow{x}$, где $\overrightarrow{y^{\prime }}$ — подмножество из $k$ элементов вектора $\overrightarrow{y}$, доступных на приёмнике.

Полиномиальная передискретизация

Пример: Неисправная электронная почта (Шаблон:Lang-en)

В случае, когда $k=2$, избыточные символы могут быть созданы как промежуточные точки на отрезке, соединяющем два исходных символа. Это показано на простом примере, называемом неисправной электронной почтой:

Алиса посчитала значения $f(1)$ и $f(2)$

Алиса хочет отправить свой телефонный номер (555629) Бобу, используя неисправную электронную почту. Данный вид почты работает так же, как обычная электронная почта, за следующим исключением:

1. Около половины всех сообщений теряются.
2. Сообщения длиннее 5 символов запрещены.
3. Это очень дорого.

Вместо того, чтобы спросить у Боба подтверждения сообщения, которое она отправила, Алиса придумывает следующую схему:

1. Она разбивает свой телефонный номер на две части $a=555,b=629$ и отправляет 2 сообщения Бобу — «A=555» и «B=629».
2. Она строит линейную функцию $f(i)=a+(b-a)(i-1)$, в этом примере $f(i)=555+74(i-1)$. Таким образом $f(1)=555$ и $f(2)=629$.
3. Она считает значения $f(3)=703,f(4)=777$ и $f(5)=851$, а затем отправляет три избыточных сообщения: «C=703», «D=777» и «E=851».

Боб знает, что выражение для $f(k)$ следующее $f(i)=a+(b-a)(i-1)$, где $a$ и $b$ — две части телефонного номера. Теперь предположим, что Боб получает «D=777» и «E=851».

Боб получает два сообщения с $f(4)$ и $f(5)$

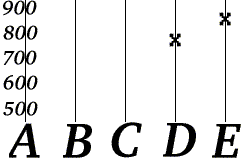
Боб может восстановить телефонный номер Алисы с помощью $a$ и $b$, используя значения $f(4)$ и $f(5)$, которые он получил. Более того, он может это сделать, используя два любых полученных сообщения. Значит, в этом примере кодовая доля равна 40 %. Заметим, что Алиса не может закодировать свой номер телефона только в одном сообщении такой почты, так как он состоит из 6 символов, а максимальная длина одного сообщения — 5 символов. Если бы она отправляла свой номер телефона по частям, запрашивая подтверждения каждой части от Боба, то было бы отправлено минимум 4 сообщения (два от Алисы и два подтверждения от Боба).

Общий случай

Приведённая выше линейная конструкция может быть обобщена до полиномиальной интерполяции. В таком случае точки теперь вычисляются над конечным полем ${𝔽}_{2^m}$, где $m$ — число бит в символе. Отправитель нумерует символы данных от $0$ до $k-1$ и посылает их. Затем он строит, например, интерполяционный многочлен Лагранжа $p(x)$ степени $k$, так что $p(i)$ равен $i$-ому символу данных. Потом он отправляет $p(k),\dots ,p(n-1)$. С помощью полиномиальной интерполяции получатель сможет восстановить потерянные данные в случае, если он успешно принял $k$ символов.

Реализация в реальном мире

Данный процесс реализован в Коде Рида — Соломона с кодовыми словами, сконструированными над конечным полем при использовании определителя Вандермонда.

Почти оптимальный стирающий код

Почти оптимальный стирающий код требует $(1+\epsilon )k$ символов, чтобы восстановить сообщение (где $\epsilon >0$). Величина $\epsilon$ может быть уменьшена за счёт дополнительного времени работы процессора. При использовании таких кодов необходимо решить, что предпочтительнее: сложность вычислений или возможность коррекции сообщений. В 2004 году существовал только один почти оптимальный стирающий код с линейным временем кодирования и декодирования — Шаблон:Не переведено 5.

Применение

Стирающие коды применяются в:

• Шаблон:Не переведено 5 (например, в группе по надёжному мультивещанию IETF)
• 3GPP (MBMS и eMBMS (Шаблон:Не переведено 5)
• одноранговых сетях, например, для решения проблемы передачи последнего блока данных
• Шаблон:Не переведено 5.

Примеры

Здесь приведены некоторые примеры различных кодов.

Почти оптимальные стирающие коды

• Код с малой плотностью проверок на чётность

Оптимальные стирающие коды

• Бит чётности
• Код Рида — Соломона

Литература

• Шаблон:Книга