Теорема Фалеса об угле, опирающемся на диаметр окружности

$\mathrm{\angle }ABC$ — прямой

Теорема об угле, опирающемся на диаметр окружности — классическая теорема планиметрии, частный случай теоремы о вписанном угле.

Формулировка

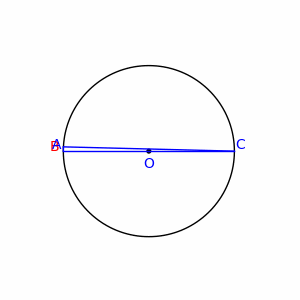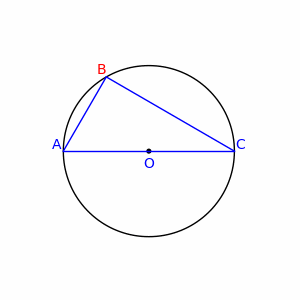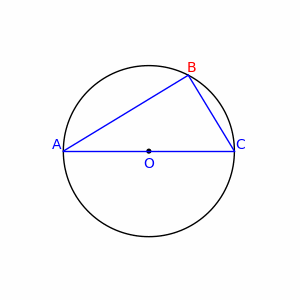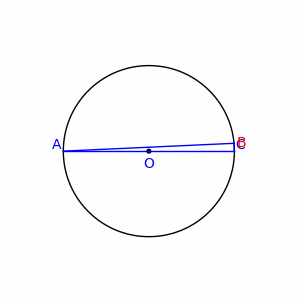
Плоский угол, опирающийся на диаметр окружности, — прямой.

Использование

Построение касательных с помощью угла, опирающегося на диаметр окружности

Используя свойство угла, опирающегося на диаметр, можно построить касательную к окружности. Пусть дана окружность $k$ и точка $P$ вне этой окружности. Построим касательные из точки $P$ к окружности $k$. Соединим центр $O$ окружности $k$ с точкой $P$ и на отрезке $OP$, как на диаметре, построим окружность. Две окружности пересекаются по двум точкам — обозначим их $T$ и $T^{\prime }$. $\mathrm{\angle }OTP$ будет прямой, так как вписанный и опирается на диаметр. $OT$ — радиус окружности $k$, перпендикулярный прямой $PT$, пересекающей окружность $k$ в точке $T$; следовательно, $PT$ — касательная. Аналогичные рассуждения можно провести о точке $T^{\prime }$.

Частный случай

• Окружность Фурмана — окружность для данного треугольника с диаметром, равным отрезку прямой, который расположен между ортоцентром и точкой Нагеля.

См. также

• Вписанный угол
• Окружность
• Теорема Фалеса
• Треугольник
• Фалес Милетский