Бета-функция

График бета-функции при вещественных аргументах

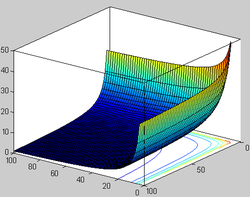
В математике бета-функцией ($\mathrm{B}$-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух комплексных переменных:

$\mathrm{B}(x,y)=\underset{0}{\overset{1}{\int }}{t}^{x-1}(1-t{)}^{y-1}dt,$

определённая при $\mathrm{Re}x>0$, $\mathrm{Re}y>0$.

Бета-функция была изучена Эйлером, ЛежандромШаблон:Когда?, а название ей дал Жак Бине.

Свойства

Бета-функция симметрична относительно перестановки переменных, то есть

$\mathrm{B}(x,y)=\mathrm{B}(y,x).$

Бета-функцию можно выразить через другие функции:

$\mathrm{B}(x,y)=\frac{\mathrm{\Gamma }(x)\mathrm{\Gamma }(y)}{\mathrm{\Gamma }(x+y)},$

где $\mathrm{\Gamma }(x)$ — Гамма-функция;

$\mathrm{B}(x,y)=2\underset{0}{\overset{\pi /2}{\int }}{\sin }^{2x-1}\theta {\cos }^{2y-1}\theta d\theta ,\mathrm{Re}x>0,\mathrm{Re}y>0;$

$\mathrm{B}(x,y)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{t^{x-1}}{(1+t{)}^{x+y}}dt,\mathrm{Re}x>0,\mathrm{Re}y>0;$

$\mathrm{B}(x,y)=\frac{1}{y}\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{(y{)}_{n+1}}{n!(x+n)},$

где $(x{)}_n$ — нисходящий факториал, равный $x\cdot (x-1)\cdot (x-2)\cdot \dots \cdot (x-n+1)$.

Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:

$(\genfrac{}{}{0ex}{}{n}{k})=\frac{1}{(n+1)\mathrm{B}(n-k+1,k+1)}.$

Бета-функция удовлетворяет двумерному разностному уравнению:

$\mathrm{B}(x,y)-\mathrm{B}(x+1,y)-\mathrm{B}(x,y+1)=0.$

Производные

Частные производные у бета-функции следующие:

$\frac{\partial }{\partial x}\mathrm{B}(x,y)=\mathrm{B}(x,y)(\frac{{\mathrm{\Gamma }}^{\prime }(x)}{\mathrm{\Gamma }(x)}-\frac{{\mathrm{\Gamma }}^{\prime }(x+y)}{\mathrm{\Gamma }(x+y)})=\mathrm{B}(x,y)(\psi (x)-\psi (x+y)),$

$\frac{\partial }{\partial y}\mathrm{B}(x,y)=\mathrm{B}(x,y)(\frac{{\mathrm{\Gamma }}^{\prime }(y)}{\mathrm{\Gamma }(y)}-\frac{{\mathrm{\Gamma }}^{\prime }(x+y)}{\mathrm{\Gamma }(x+y)})=\mathrm{B}(x,y)(\psi (y)-\psi (x+y)),$

где $\psi (x)$ — дигамма-функция.

Неполная бета-функция

Неполная бета-функция — это обобщение бета-функции, заменяющее интеграл по отрезку $[0,1]$ на интеграл с переменным верхним пределом:

${\mathrm{B}}_x(a,b)=\underset{0}{\overset{x}{\int }}{t}^{a-1}(1-t{)}^{b-1}dt.$

При $x=1$ неполная бета-функция совпадает с полной.

Регуляризованная неполная бета-функция определяется через полную и неполную бета-функции:

$I_x(a,b)=\frac{{\mathrm{B}}_x(a,b)}{\mathrm{B}(a,b)}.$

Свойства $I(x)$

$I_0(a,b)=0,$

$I_1(a,b)=1,$

$I_x(a,b)=1-I_{1-x}(b,a),$

$I_x(a+1,b)=I_x(a,b)-\frac{x^a(1-x{)}^b}{aB(a,b)}.$

Литература

Кузнецов Д. С. Специальные функции (1962) — 249 с.

См. также

• Список объектов, названных в честь Леонарда Эйлера
• Гамма-функция
• Бета-распределение