Коуравнитель

Коуравнитель — теоретико-категорное обобщение понятия фактора по отношению эквивалентности. Это понятие двойственно к понятию уравнителя, отсюда и название.

Определение

Коуравнитель — это копредел диаграммы, состоящей из двух объектов — Шаблон:Math и Шаблон:Math, и двух параллельных морфизмов Шаблон:Math, Шаблон:Math.

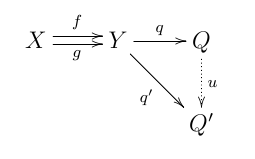
Более явно, коуравнитель — это объект Шаблон:Math вместе с морфизмом Шаблон:Math, таким что Шаблон:Math. Более того, пара Шаблон:Math обладает универсальным свойством: для любой другой пары Шаблон:Math с тем же свойством существует единственный морфизм Шаблон:Math, замыкающий следующую диаграмму до коммутативной:

Как и любые универсальные конструкции, коуравнитель, если существует, определен с точностью до изоморфизма. Можно показать, что коуравнитель Шаблон:Math является эпиморфизмом в любой категории.

Примеры

• В категории множеств коуравнитель двух функций Шаблон:Math — это фактор Шаблон:Math по наиболее слабому отношению эквивалентности $\sim$, такому что для любого $x\in X$, верно $f(x)\sim g(x)$.
• В категории групп ситуация очень похожа: если Шаблон:Math — гомоморфизмы групп, их коуравнитель — это фактор Шаблон:Math по нормальному замыканию множества:

  $S=\{f(x)g(x{)}^{-1}|x\in X\}$.

• Для абелевых групп коуравнитель особенно прост. Это просто факторгруппа Шаблон:Math (коядро морфизма Шаблон:Math).
• В категории топологических пространств окружность $S^1$ можно рассматривать как коуравнитель двух вложений стандартного 0-мерного симплекса в стандартный 1-мерный симплекс.
• Коуравнители могут быть довольно большими: существует ровно два функтора из категории 1 с одним объектом и одним морфизмом, в категорию 2 с двумя объектами и ровно одним нетождественным морфизмом. Коуравнитель этих функторов — моноид натуральных чисел по сложению, рассматриваемый как категория из одного элемента. Это показывает, что хотя каждый коуравнитель эпиморфен, он не обязательно сюръективен.

Литература

• Шаблон:Книга:Категории для работающего математика