Множество больших тригонометрических сумм

Множество больших тригонометрических сумм — понятие теории чисел — множество индексов, в которых преобразование Фурье характеристической функции заданного подмножества группы принимает достаточно большие значения.

Для удобства изложения далее в статье используется сокращение МБТС, хотя оно не является общепринятым.

Предпосылки к изучению

В классическом методе тригонометрических сумм часто требуется оценить сверху значение модуля суммы $\sum _{x\in X}{e}^{\frac{ax}{n}}$ для некоторого подмножества $X\subset {\mathbb{Z}}_n$ циклической группы. Если эта сумма имеет малый модуль при всех $a\equiv ̸0(\mathrm{mod}n)$, то из этого можно сделать выводы о равномерности распределения $X$ среди непрерывных отрезков вычетов по модулю $n$. Это оказывается верным, например, для множества квадратичных вычетовШаблон:Sfn (и вообще степенных вычетовШаблон:Sfn), дискретных логарифмов последовательных чиселШаблон:Sfn или (для простых $n$) выражений вида $a+a^{-1}$, где $a^{-1}$ — обратный элемент ${𝔽}_n$ относительно умножения (суммы Клоостермана)Шаблон:Sfn.

Естественным образом возникает вопрос: если не для всех $a\equiv ̸0(\mathrm{mod}n)$ рассматриваемые суммы имеют малый модуль, то для сколь многих $a$ этот модуль может быть очень большим, и для каких именно наборов значений $a$ это может выполняться? Например, очевидно, что если это выполняется для $a$, то и для $-a$ тоже, но возникает вопрос о существовании других таких всеобщих закономерностей, не зависящих от природы множества $X$.

Данный вопрос нашёл широкое рассмотрение в аддитивной комбинаторике, идеей которой и является выявление закономерностей в структуре множеств при минимальных ограничениях на них, а коэффициенты Фурье находят в ней широкое применение.

Определение

Закономерности, касающиеся МБТС, рассматриваются, как правило, исходя из двух параметров — размера основного множества и границы, по которой отделяются значения тригонометрических сумм. Иногда для удобства границу на тригонометрические суммы записывают не в явном виде, а параметризуют через её отношение к размеру множества (поскольку модуль суммы, очевидно, никогда не больше размера множества). Из-за этого, а также от различной нормировки коэффициентов Фурье, выражения в формулировках определений и теорем у разных авторов могут различаться, но суть исследуемых соотношений остаётся той же.

Шаблон:Рамка Пусть $N$ — натуральное число, $A\subset {\mathbb{Z}}_N$, $|A|=\delta N$

Пусть также $\hat{A}(\xi )=\sum _{x\in A}{e}^{2\pi \frac{\xi x}{N}i}$ обозначает $\xi$-й коэффициент Фурье (не нормированный) характеристической функции $A$.

Тогда множества больших тригонометрических сумм с параметром определяются (с точностью до параметра $\alpha$) как

${ℛ}_{\alpha }={ℛ}_{\alpha }(A)=\left\{\xi :|\hat{A}(\xi )|\ge \alpha N\right\}$Шаблон:Sfn

Некоторые приёмы изучения

Приближение функции множеством

Для построения примеров множеств, обладающих МБТС с теми или иными свойствами, часто строятся функции, обладающие соответствующие коэффициентами Фурье, а потом на этом основании констатируется существование множеств, коэффициенты Фурье которых не сильно отличаются от коэффициентов этих функцийШаблон:SfnШаблон:SfnШаблон:Sfn. Основания для этого даёт следующая лемма, доказательство которой восходит к общей линейно-алгебраической идее и выходит за рамки науки о МБТС.

Шаблон:Рамка Если $f:{\mathbb{Z}}_N\to [0;1]$, то существует множество $S\subset {\mathbb{Z}}_N$ размера $\lfloor \sum _{x}f(x)\rfloor$ такое, что $\mathrm{\forall }r\in {\mathbb{Z}}_N:|\hat{S}(r)-\hat{f}(r)|\le 20\sqrt{N}$Шаблон:Sfn Шаблон:Конец рамки

Изменение индикаторной функции при фильтрации коэффициентов Фурье по различным значениям $\alpha$

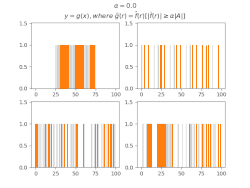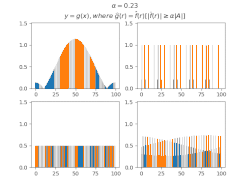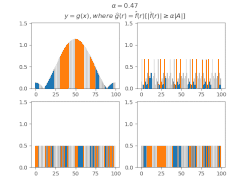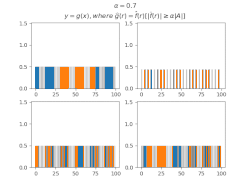
Фильтрация коэффициентов Фурье

Для вывода общих утверждений об МБТС некоторых множеств удобно использоватьШаблон:Sfn функции, образованные из индикаторной функции множества фильтрацией коэффициентов Фурье по этому МБТС, то есть такую функцию $f$, что

$\hat{f}(\xi )=\{\begin{array}{cc}\widehat{1_A}(\xi )& \xi \in {ℛ}_{\alpha }(A)\\ 0& \xi \in ̸{ℛ}_{\alpha }(A)\end{array}$

Оказывается, что у таких функций большая часть суммы значений также концентрируется в $A$.

Свойства

Размер

Из равенства $\sum _{\xi }|\hat{A}(\xi ){|}^2=|A{|}^2$ легко получается. что $|{ℛ}_{\alpha }|<\frac{\delta }{{\alpha }^2}$.

Для некоторых значений $\delta ,\alpha$ эта оценка достаточно точна по порядку роста.

Пример — квадратичные вычеты

Если $Q_p\subset {\mathbb{Z}}_p$ — множество квадратичных вычетов по простому модулю $p$, $\delta =\frac{p+1}{2p},\alpha \approx \frac{1}{2\sqrt{p}}$, то для $|{ℛ}_{\alpha }(Q_p)|=p$ оценка превращается в неравенство близкое к $|{ℛ}_{\alpha }(Q_p)|<2(p+1)$.

С помощью конструкции вида $\bigcup _{s=0}^{k-1}(sp+Q_p)\subset {\mathbb{Z}}_{kp}$ эту идею можно обобщить на МБТС с меньшей относительно модуля границей на значение суммы. При этом между оценкой и реальным размером МБТС образуется та же разница.

Пример — подряд идущие числа

В примере с квадратичными вычетами величина $\delta =\frac{p+1}{2p}\approx \frac{1}{2}$ близка к фиксированной. Чтобы найти примеры с произвольной величиной $\delta$, достаточно рассмотреть множество $A=\{1,2,\dots ,m\}\subset {\mathbb{Z}}_N$, где $m\ll N$.

Тогда $\mathrm{\forall }\xi <\frac{N}{4m}\mathrm{\forall }a\in A:\arg \left(e^{2\pi \frac{\xi a}{N}i}\right)<\frac{\pi }{2}$ (то есть направления векторов, соответствующих $e^{2\pi \frac{\xi a}{N}i}$, ограничены довольно узким углом) и поэтому $\mathrm{\forall }\xi <\frac{N}{4m}:|\hat{A}(\xi )|\gg \frac{m}{2}$, так что верна оценка снизу $|{ℛ}_{\frac{m}{2N}}(A)|\ge \lfloor \frac{N}{4m}\rfloor$. Более того, так как $|\hat{A}(\xi )|=|\hat{A}(-\xi )|$, то верно даже, что $|{ℛ}_{\frac{m}{2N}}(A)|\ge \lfloor \frac{N}{2m}\rfloor$

Однако при $\delta =\frac{m}{N},\alpha =\frac{m}{2N}$ оценка сверху превращается в неравенство $|{ℛ}_{\alpha }(A)|\le 4\frac{N}{m}$.

Получается, что $\lfloor \frac{N}{2m}\rfloor \le |{ℛ}_{\alpha }(A)|\le 4\frac{N}{m}$ и оценка сверху также точна до умножения на константу.

Структура

Степень структурированности МБТС в разных смыслах может быть оценена достаточно точна когда они достаточно велики. В случае, когда они имеют малый размер, МБТС могут быть вполне произвольными.

Аддитивная энергия

С одной стороны, МБТС допускают нижнюю оценку на аддитивную энергию любого своего подмножества.

Шаблон:Рамка Если $B\subset {ℛ}_{\alpha }$, то $T_k(B){\gg }_k\frac{{\alpha }^{2k}}{{\delta }^{2k-1}}|B{|}^{2k}$ Шаблон:Конец рамки

С другой стороны, при некоторых дополнительных (не слишком сильных) условиях на параметры $k,\alpha ,\delta$ существует множество $A$, для которого верна и верхняя оценка $T_k({ℛ}_{\alpha }){\ll }_k\frac{\delta }{{\alpha }^{2k}}$, причём $|{ℛ}_{\alpha }|\gg \frac{\delta }{{\alpha }^2}$Шаблон:Sfn. Это говорит о том, что иногда МБТС могут быть всё-таки достаточно большими и бесструктурными одновременно.

В случае, когда ${ℛ}_{\alpha }$ имеет максимально возможный размер, эти оценки (если первую рассматривать для $B={ℛ}_{\alpha }$) совпадают с точностью до константы, зависящей от $k$. То есть для довольно широкого класса значений параметров $\delta ,\alpha$ существуют множества, мера структурированности МБТС которых определена почти однозначно, причём их МБТС оказываются тем более бесструктурны, чем больше в них элементов (чем больше разница между $\delta$ и $\alpha$).

Аддитивная размерность

Другая изучаемая характеристика — аддитивная размерность МБТС, то есть размер максиимального содержащегося в нём диссоциативного множества. Далее эта величина обозначается как ${\dim }_{+}({ℛ}_{\alpha })$.

Чанг в 2002 году доказала, что ${\dim }_{+}({ℛ}_{\alpha })\ll {\left(\frac{\delta }{\alpha }\right)}^2\log \left(\frac{1}{\delta }\right)$Шаблон:SfnШаблон:Sfn. Основу доказательства составляло применение неравенства Рудина к функции, образованной из индикаторной функции множества фильтрацией коэффициентов Фурье по ${ℛ}_{\alpha }$.

В то же время Грин в 2003 году показал, что при условиях

• $\delta \le \frac{1}{8}$

• $\alpha \le \frac{\delta }{32}$

• ${\left(\frac{\delta }{\alpha }\right)}^2\log \left(\frac{1}{\delta }\right)\le \frac{\log N}{\log \log N}$

существует множество $A$, для которого ${\dim }_{+}({ℛ}_{\alpha })\gg {\left(\frac{\delta }{\alpha }\right)}^2\log \left(\frac{1}{\delta }\right)$Шаблон:Sfn.

То есть при рассмотрении достаточно больших значений сумм аддитивную размерность МБТС также можно оценить достаточно точно.

Произвольность

Если МБТС достаточно мало́ по сравнению со своим максимально возможным размером, то общая оценка на аддитивную энергию оказывается тривиальной, то есть не позволяет ничего сказать о внутренней структуре множества.

Оказывается, что в этом случае о ней ничего сказать и нельзя — то есть произвольное множество может быть малым МБТС.

Шаблон:Рамка Теорема (Шкредов)

Если

• $\delta <\frac{1}{2}$

• $20\frac{1}{\sqrt{N}}<\alpha \le \frac{\delta }{2}$

• $|S|\le \frac{\delta }{2\alpha }$

• $S=-S$

то $\mathrm{\exists }A:|A|=\lfloor \delta N\rfloor$ и ${ℛ}_{\alpha }(A)=S$ Шаблон:Конец рамки

Основным ограничением здесь служит $|S|\le \frac{\delta }{2\alpha }$ — остальные обусловлены общей природой тригонометрических сумм.

Ограничение на размер может быть ослаблено до $|S|\le \frac{\delta }{\alpha }\log \frac{1}{\delta }$ если добавить условие на то, что $S$ обладает некоторым свойством, являющимся вариацией диссоциативностиШаблон:Sfn.

Связь между МБТС разных множеств

МБТС множеств размера $\lfloor \frac{N}{2}\rfloor$ (половина размера группы) в некотором смысле покрывают структуру всех остальных МБТС.

Шаблон:Рамка Теорема (Грин)

Если $\alpha \ge 80\frac{1}{\sqrt{N}}$, то для всякого $A\subset {\mathbb{Z}}_N$ существует $B\subset {\mathbb{Z}}_N$ такое, что $|B|=\lfloor \frac{N}{2}\rfloor$ и ${ℛ}_{\alpha }(A)\subset {ℛ}_{\frac{\alpha }{4}}(B)$ Шаблон:Конец рамки

Обобщения

МБТС могут изучаться не только для циклических, но и для любых групп если правильным образом обобщить понятие коэффициента ФурьеШаблон:Sfn.

Например, для любого $\alpha <\frac{1}{2}$ и множества $A\subset {\mathbb{Z}}_2^n$ его $\alpha$-МБТС содержит в себе подгруппу размера ${}^{\left(\frac{1}{{\alpha }^3}\right)}2$ (последнее выражение означает тетрацию)Шаблон:Sfn.

Приложения

Чанг применила оценки на аддитивную размерность МБТС к улучшению оценок в теореме ФрейманаШаблон:Sfn.

Литература

• Шаблон:Статья

• Шаблон:Статья

• Шаблон:Статья

• Шаблон:Статья

• Шаблон:Статья

• Шаблон:Статья

• Шаблон:Статья