Тензорное произведение

Шаблон:Значения Тензорное произведение — операция над векторными пространствами, а также над элементами (векторами, матрицами, операторами, тензорами и т. д.) перемножаемых пространств.

Тензорное произведение линейных пространств $A$ и $B$ есть линейное пространство, обозначаемое $A\otimes B$. Для элементов $a\in A$ и $b\in B$ их тензорное произведение $a\otimes b$ лежит в пространстве $A\otimes B$.

Обозначение тензорного произведения произошло по аналогии с обозначением для декартова произведения множеств.

Тензорное произведение линейных (векторных) пространств

Конечномерные пространства

Пусть $A$ и $B$ — конечномерные векторные пространства над полем $K$, $\{e_i{\}}_{i=1\dots n}$ — базис в $A$, $\{f_k{\}}_{k=1\dots m}$ — базис в $B$. Тензорным произведением $A\otimes B$ пространств $A$ и $B$ будем называть векторное пространство, порождённое элементами $e_i\otimes f_k$, называемыми тензорными произведениями базисных векторов. Тензорное произведение $a\otimes b$ произвольных векторов $a\in A,b\in B$ можно определить, полагая операцию $\otimes$ билинейной:

$(\lambda a_1+\mu a_2)\otimes b=\lambda a_1\otimes b+\mu a_2\otimes b,\lambda ,\mu \in K$

$a\otimes (\lambda b_1+\mu b_2)=\lambda a\otimes b_1+\mu a\otimes b_2,\lambda ,\mu \in K$

При этом тензорное произведение произвольных векторов $a$ и $b$ выражается как линейная комбинация базисных векторов $e_i\otimes f_k$. Элементы в $A\otimes B$, представимые в виде $a\otimes b$, называются разложимыми.

Хотя тензорное произведение пространств определяется через выбор базисов, его геометрические свойства не зависят от этого выбора.

Определение с помощью универсального свойства

Тензорное произведение — это в некотором смысле наиболее общее пространство, в которое можно билинейно отобразить исходные пространства. А именно, для любого другого пространства $C$ и билинейного отображения ${\otimes }^{\prime }:A\times B\to C$ существует единственное линейное отображение $f:A\otimes B\to C$ такое, что

${\otimes }^{\prime }=f\circ \otimes ,$

где $\circ$ обозначает композицию функций.

В частности, отсюда следует, что тензорное произведение не зависит от выбора базисов в $A$ и $B$, так как все удовлетворяющие универсальному свойству пространства $A\otimes B$ оказываются канонически изоморфны.

Таким образом, задание произвольного билинейного отображения $L^2\ni \phi :A\times B\to C$ эквивалентно заданию линейного отображения $L\ni \phi :A\otimes B\to C$: пространства $L^2(A\times B,C)$ и $L(A\otimes B,C)$ являются канонически изоморфными.

Произведение более чем двух пространств

Приведенное универсальное свойство может быть продолжено на произведения более чем двух пространств. Например, пусть $V_1$, $V_2$, и $V_3$ — три векторных пространства. Тензорное произведение $V_1\otimes V_2\otimes V_3$ вместе с трилинейным отображением из прямого произведения

$\phi :V_1\times V_2\times V_3\to V_1\otimes V_2\otimes V_3$

имеет такой вид, что любое трилинейное отображение $F$ из прямого произведения в векторное пространство $W$

$F:V_1\times V_2\times V_3\to W$

единственным образом пропускается через тензорное произведение:

$F=L\circ \phi$

где $L$ — линейное отображение. Тензорное произведение характеризуется этим свойством однозначно, с точностью до изоморфизма. Результат приведенной конструкции совпадает с повторением тензорного произведения двух пространств. Например, если $V_1$, $V_2$ и $V_3$ — три векторных пространства, то существует (естественный) изоморфизм

$V_1\otimes V_2\otimes V_3\cong V_1\otimes (V_2\otimes V_3)\cong (V_1\otimes V_2)\otimes V_3.$

В общем случае тензорное произведение произвольного индексированного семейства множеств $V_i$, $i\in I$ определяется как универсальный объект для полилинейных отображений из прямого произведения $\prod _{i\in I}{V}_i$.

Пусть $n$ — произвольное натуральное число. Тогда $n$-й тензорной степенью пространства $V$ называется тензорное произведение $n$ копий $V$:

$V^{\otimes n}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\underset{n}{\underbrace{V\otimes \cdots \otimes V}}.$

Функториальность

Тензорное произведение действует также на линейных отображениях. Пусть $A:U_1\to U_2$, $B:W_1\to W_2$ — линейные операторы. Тензорное произведение операторов $A\otimes B:U_1\otimes W_1\to U_2\otimes W_2$ определяется по правилу

$(A\otimes B)(u\otimes w)=(Au)\otimes (Bw),u\in U_1,w\in W_1$

После этого определения тензорное произведение становится бифунктором из категории векторных пространств в себя, ковариантным по обоим аргументам.

Если матрицы операторов A и B при некотором выборе базисов имеют вид

$\mathrm{A}=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{m1}& \cdots & a_{mn}\end{array}\right]$

$\mathrm{B}=\left[\begin{array}{ccc}{b}_{11}& \cdots & b_{1q}\\ ⋮& \ddots & ⋮\\ b_{p1}& \cdots & b_{pq}\end{array}\right]$

то матрица их тензорного произведения запишется в базисе, образованном тензорным произведением базисов, в виде блочной матрицы

$\mathrm{A}\otimes \mathrm{B}=\left[\begin{array}{ccc}{a}_{11}B& \cdots & a_{1n}B\\ ⋮& \ddots & ⋮\\ a_{m1}B& \cdots & a_{mn}B\end{array}\right]=$

$=\left[\begin{array}{cccccccccc}{a}_{11}{b}_{11}& a_{11}{b}_{12}& \cdots & a_{11}{b}_{1q}& \cdots & \cdots & a_{1n}{b}_{11}& a_{1n}{b}_{12}& \cdots & a_{1n}{b}_{1q}\\ a_{11}{b}_{21}& a_{11}{b}_{22}& \cdots & a_{11}{b}_{2q}& \cdots & \cdots & a_{1n}{b}_{21}& a_{1n}{b}_{22}& \cdots & a_{1n}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{11}{b}_{p1}& a_{11}{b}_{p2}& \cdots & a_{11}{b}_{pq}& \cdots & \cdots & a_{1n}{b}_{p1}& a_{1n}{b}_{p2}& \cdots & a_{1n}{b}_{pq}\\ ⋮& ⋮& & ⋮& \ddots & & ⋮& ⋮& & ⋮\\ ⋮& ⋮& & ⋮& & \ddots & ⋮& ⋮& & ⋮\\ a_{m1}{b}_{11}& a_{m1}{b}_{12}& \cdots & a_{m1}{b}_{1q}& \cdots & \cdots & a_{mn}{b}_{11}& a_{mn}{b}_{12}& \cdots & a_{mn}{b}_{1q}\\ a_{m1}{b}_{21}& a_{m1}{b}_{22}& \cdots & a_{m1}{b}_{2q}& \cdots & \cdots & a_{mn}{b}_{21}& a_{mn}{b}_{22}& \cdots & a_{mn}{b}_{2q}\\ ⋮& ⋮& \ddots & ⋮& & & ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{p1}& a_{m1}{b}_{p2}& \cdots & a_{m1}{b}_{pq}& \cdots & \cdots & a_{mn}{b}_{p1}& a_{mn}{b}_{p2}& \cdots & a_{mn}{b}_{pq}\end{array}\right]$

Соответствующая операция над матрицами называется кронекеровским произведением, по имени Леопольда Кронекера.

Частные случаи

Тензорное произведение двух векторов

(Матричное) умножение вектора-столбца справа на вектор-строку описывет их тензорное произведение:

$𝐚\otimes 𝐛\leftrightarrow \left[\begin{array}{c}{a}_1\\ a_2\\ a_3\\ a_4\end{array}\right]\left[\begin{array}{ccc}{b}_1& b_2& b_3\end{array}\right]=\left[\begin{array}{ccc}{a}_1{b}_1& a_1{b}_2& a_1{b}_3\\ a_2{b}_1& a_2{b}_2& a_2{b}_3\\ a_3{b}_1& a_3{b}_2& a_3{b}_3\\ a_4{b}_1& a_4{b}_2& a_4{b}_3\end{array}\right].$

Свойства

• $\dim A\otimes B=\dim A\cdot \dim B$

Следующие алгебраические свойства основаны на каноническом изоморфизме:

• Ассоциативность

$(A\otimes B)\otimes C\simeq A\otimes (B\otimes C)$

• Формально говоря, тензорное произведение не коммутативно, но существует естественный изоморфизм $A\otimes B\to B\otimes A$
• Линейность

$A\otimes (B\oplus C)\simeq (A\otimes B)\oplus (A\otimes C)$

$\oplus$ — внешняя сумма линейных пространств.

Тензорное произведение модулей

Пусть $A_1,A_2,\dots ,A_n$ — модули над некоторым коммутативным кольцом $R$. Тензорным произведением модулей называется модуль $B$ над $R$, данный вместе с полилинейным отображением $f:A_1\times \dots \times A_n\to B$ и обладающий свойством универсальности, то есть такой, что для всякого модуля $C$ над $R$ и любого полилинейного отображения $g:A_1\times \dots \times A_n\to C$ существует единственный гомоморфизм модулей $h:B\to C$ такой, что диаграмма

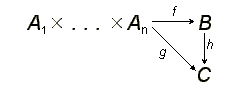
коммутативна. Тензорное произведение обозначается $A_1\otimes \dots \otimes A_n$. Из универсальности тензорного произведения следует, что оно определено однозначно с точностью до изоморфизма.

Для доказательства существования тензорного произведения любых модулей над коммутативным кольцом построим свободный модуль $M$, образующими которого будут n-ки элементов модулей $(x_1,\dots ,x_n)$ где $x_i\in A_i$. Пусть $N$ — подмодуль $M$, порождаемый следующими элементами:

1. $(x_1,\dots ,x_i+y_i,\dots ,x_n)-(x_1,\dots ,x_i,\dots ,x_n)-(x_1,\dots ,y_i,\dots ,x_n)$
2. $(x_1,\dots ,\lambda x_i,\dots ,x_n)-\lambda (x_1,\dots ,x_i,\dots ,x_n)$

Тензорное произведение определяется как фактормодуль $B=M/N$, класс $(x_1,\dots ,x_n)+N$ обозначается $x_1\otimes \dots \otimes x_n$, и называется тензорным произведением элементов $x_i$, a $f$ определяется как соответствующее индуцированное отображение.

Из 1) и 2) следует что отображение $f:A_1\times \dots \times A_n\to B$ полилинейно. Докажем, что для любого модуля $C$ и любого полилинейного отображения $g:A_1\times \dots \times A_n\to C$ существует единственный гомоморфизм модулей $h$, такой, что $g=h\circ f$.

В самом деле, так как $M$ свободен, то существует единственное отображение $h^{*}$, делающее диаграмму

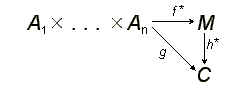
коммутативной, а в силу того, что $g$ полилинейно, то на $N$ $h^{*}(N)=0$, отсюда, переходя к индуцированному отображению, получаем, что $h:M/N\to C$, будет тем самым единственным гомоморфизмом, существование которого и требовалось доказать.

Элементы $A_1\otimes \dots \otimes A_n$, представимые в виде $x_1\otimes \dots \otimes x_n$, называются разложимыми.

Если $f_i:A_i\to B_i$ — изоморфизмы модулей, то индуцированный гомоморфизм, соответствующий билинейному отображению

$f_1\otimes \dots \otimes f_n:A_1\otimes \dots \otimes A_n\to B_1\otimes \dots \otimes B_n$

существующий по свойству универсальности, называется тензорным произведением гомоморфизмов $f_i$.

Особенно простой случай получается в случае свободных модулей. Пусть $e_{i1},\dots ,e_{in}$ — базис модуля $A_i$. Построим свободный модуль $F$ над нашим кольцом, имеющий в качестве базиса элементы, соответствующие n-кам $(e_{1m},e_{2p},\dots ,e_{ns})$, определив отображение $f(e_{1m},e_{2p},\dots ,e_{ns})\to (e_{1m},e_{2p},\dots ,e_{ns})$ и распространив его на $A_1\times \dots \times A_n$ по линейности. Тогда $F$ является тензорным произведением, где $(e_{1m},e_{2p},\dots ,e_{ns})$ является тензорным произведением элементов $e_{1m}\otimes e_{2p}\otimes \dots \otimes e_{ns}$. Если число модулей и все их базисы конечны, то

$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(A_1\otimes \dots \otimes A_n)=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}{A}_1\cdot \dots \cdot \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}{A}_n$.

Литература

• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга

См. также

• Свёртка тензора
• Тензор
• Тензорное поле
• Тензорная алгебра
• Тензорное произведение графов