Расслоённое произведение

Расслоённое произведение (рассло́енное произведение, послойное произведение, коамальгама, декартов квадрат, Шаблон:Lang-en) — теоретико-категорное понятие, определяемое как предел диаграммы, состоящей из двух морфизмов: $X\to Z\leftarrow Y$. Расслоённое произведение часто обозначают как $X{\times }_{Z}Y$.

Двойственное понятие — кодекартов квадрат.

Универсальное свойство

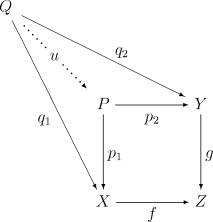
Для пары морфизмов $f:X\to Z$ и $g:Y\to Z$ в категории $C$ расслоённое произведение $X$ и $Y$ над $Z$ — это объект $P=X{\times }_{Z}Y$ вместе с морфизмами $p_1,p_2,$ для которых следующая диаграмма коммутативна:

Более того, расслоённое произведение должно быть универсальным объектом с таким свойством: для любого объекта $Q$ с парой морфизмов $q_1:Q\to X$ и $q_2:Q\to Y$, дополняющих пару $(f,g)$ до коммутативного квадрата, существует единственный морфизм $u:Q\to P$ такой, что коммутативна диаграмма:

Внутренний квадрат этой диаграммы, образованный морфизмами $f$, $g$, $p_1$, $p_2$ называется декартовым (или коуниверсальным) квадратом для пары морфизмов $f$ и $g$.

Как и другие объекты, определённые с помощью универсального свойства, расслоённое произведение не обязательно существует, но если существует, то определено с точностью до изоморфизма.

Примеры

В категории множеств расслоённое произведение множеств $X$ и $Y$ с отображениями $f:X\to Z$ и $g:Y\to Z$ — это множество:

$X{\times }_{Z}Y=\{(x,y)\in X\times Y|f(x)=g(y)\}$

вместе с естественными проекциями на компоненты.

Аналогичным образом определяется расслоённое произведение в категории коммутативных колец.

Также расслоённое произведение в $𝐒𝐞𝐭$ можно описывать двумя асимметричными способами:

$X{\times }_{Z}Y$

$\cong \underset{x\in X}{⨆}{g}^{-1}[\{f(x)\}]$

$\cong \underset{y\in Y}{⨆}{f}^{-1}[\{g(y)\}]$,

где $⨆$ — дизъюнктное объединение множеств.

См. также

• Индуцированное расслоение

Литература

• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга:Категории для работающего математика
• Шаблон:Книга
• Шаблон:Книга