Огибающая

Огибающая семейства прямых.

Кривая $\gamma$ называется огиба́ющей семейства кривых ${\gamma }_{\alpha }$, зависящих от параметра $\alpha$, если она в каждой своей точке касается хотя бы одной кривой семейства и каждым своим отрезком касается бесконечного множества этих кривых.

Определение

Пусть имеется семейство кривых ${\gamma }_{\alpha }$, зависящих от параметра $\alpha$ и задающихся уравнением: $F(\alpha ,x,y)=0$. Тогда огибающая семейства кривых определяется как геометрическое множество точек $(x,y)$, для которых существует значение $\alpha$, для которого выполнено оба равенства:

$F(\alpha ,x,y)=\frac{\partial F}{\partial \alpha }(\alpha ,x,y)=0,$

где $\frac{\partial F}{\partial \alpha }$ — частная производная функции $F$ по параметру $\alpha$.

Примеры

• Для семейства окружностей одинакового радиуса с центрами на прямой огибающая состоит из двух параллельных прямых.
• Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.
• Парабола является огибающей семейства срединных перпендикуляров для отрезков, соединяющих фиксированную точку (фокус параболы) и фиксированную прямую (директрису параболы).

Прямые Симсона (красным цветом) являются касательными к дельтоиде Штейнера (синим цветом).

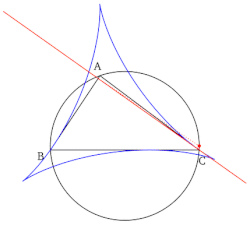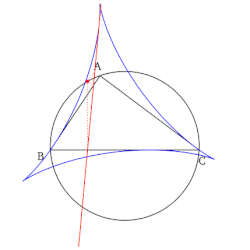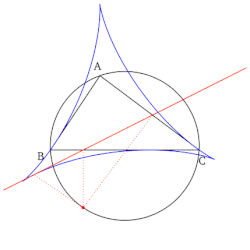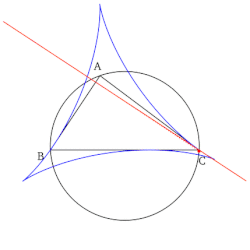
• Огибающая семейства прямых Симсона данного треугольника есть дельтоида — так называемая дельтоида Штейнера.

См. также

• Двойственная кривая
• Каустика
• Параллельная кривая

Литература

• Шаблон:Книга