Четверная группа Клейна

Шаблон:Не путать Четверна́я гру́ппа Кле́йна — нециклическая конечная коммутативная группа четвёртого порядка, играет важную роль в общей алгебре, комбинаторике и геометрии. Обычно обозначается $V$ или $V_4$ (от Шаблон:Lang-de — четверная группа). Впервые описана и исследована Феликсом Клейном в 1884 году.

• 
  Граф циклов четверной группы Клейна
• 
  Граф Кэли четверной группы Клейна

Бинарная операция между элементами $\{1,a,b,ab\}$ (единица — нейтральный элемент группы) задаётся следующей таблицей КэлиШаблон:Sfn:

$\begin{array}{ccccc}\cdot & 1& a& b& ab\\ 1& 1& a& b& ab\\ a& a& 1& ab& b\\ b& b& ab& 1& a\\ ab& ab& b& a& 1\end{array}$

Порядок каждого элемента, отличного от единицы, равен 2, поэтому группа не является циклической. Является прямым произведением циклических групп второго порядка $C_2\times C_2$; наименьшей по порядку нециклической группой.

Является простейшей группой диэдра $D_2$. Любая группа четвёртого порядка изоморфна либо циклической группе, либо четверной группе Клейна. Симметрическая группа $S_4$ имеет, кроме себя самой и единичной подгруппы, лишь две нормальные подгруппы — знакопеременную группу $A_4$ и четверную группу Клейна $V_4$, состоящую из подстановок $(),(12)(34),(13)(24),(14)(23)$.

Симметрии ромба

Встречается во многих разделах математики, примеры изоморфных ей групп:

• множество $\{0,1,2,3\}$ с операцией побитовое исключающее ИЛИ;
• приведённая система вычетов по модулю 8, состоящая из классов 1, 3, 5, 7 и по модулю 12, состоящая из классов 1, 5, 7, 11;
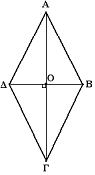
• группа симметрий ромба в трёхмерном пространстве, состоящая из 4 преобразований: тождественное, поворот на $180^{\circ }$ и два отражения относительно диагоналейШаблон:Sfn.
• группа поворотов тетраэдра на угол $\pi$ вокруг всех трёх рёберных медиан (вместе с тождественным поворотом)Шаблон:Sfn.

Литература

• Шаблон:Книга
• Шаблон:Книга