Полилогарифм

Материал из testwiki
Перейти к навигации Перейти к поиску

Полилогарифм — специальная функция, обозначаемая Lis(z) и определяемая как бесконечный степенной ряд

Lis(z)=∑k=1∞zkks,

где s и z — комплексные числа, причём |z|<1. Для иных z делается обобщение с помощью аналитического продолжения.

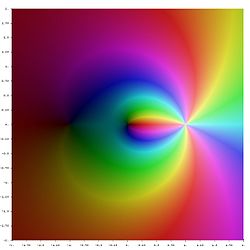
  • Карта высот полилогарифма на комплексной плоскости
  • Li−3(z)
    Li−3(z)
  • Li−2(z)
    Li−2(z)
  • Li−1(z)
    Li−1(z)
  • Li0(z)
    Li0(z)
  • Li1(z)
    Li1(z)
  • Li2(z)
    Li2(z)
  • Li3(z)
    Li3(z)

Частным случаем является s=1, при котором Li1(z)=−ln⁡(1−z). Функции Li2(z) и Li3(z) получили названия дилогарифма и трилогарифма соответственно. Для полилогарифмов различных порядков справедливо соотношение

Lis+1(z)=∫0zLis(t)tdt.

Альтернативными определениями полилогарифма являются интегралы Ферми — Дирака и Бозе — Эйнштейна.

Частные значения

Li1(12)=ln⁡2
Li2(12)=112π2−12(ln⁡2)2
Li3(12)=16(ln⁡2)3−112π2ln⁡2+78ζ(3) (где ζ(3) — постоянная Апери)
Li1(z)=−ln⁡(1−z)
Li0(z)=z1−z
Li−1(z)=z(1−z)2
Li−2(z)=z(1+z)(1−z)3
Li−3(z)=z(1+4z+z2)(1−z)4
Li−4(z)=z(1+z)(1+10z+z2)(1−z)5.

Литература

Ссылки

Шаблон:Rq

Источник — https://ru.wiki.beta.math.wmflabs.org/w/index.php?title=Полилогарифм&oldid=9777