Эвольвента

Две параллельные эвольвенты окружности — боковые части профиля в зубчатом колесе с эвольвентным зацеплением

Анимация построения эвольвенты окружности — эвольвента как разматывающаяся нить

Эвольве́нта (от Шаблон:Lang-la, родительный падеж evolventis «разворачивающий»Шаблон:SfnШаблон:Sfn), или инволю́таШаблон:Sfn, или развёрткаШаблон:Sfn, плоской кривой $L$ — это плоская кривая $L_{*}$, по отношению к которой $L$ является эволютойШаблон:SfnШаблон:SfnШаблон:Sfn.

То есть эвольвента — кривая, нормаль в каждой точке которой есть касательная к исходной кривой, иными словами, эвольвента — ортогональная траектория касательных к исходной кривойШаблон:Sfn.

Эвольвента плоской кривой также может быть определена следующим образом:

• эвольвента — траектория конца натянутой нити, которая либо наматывается на исходную кривую, либо разматывается с неё (этим объясняется другое название эвольвенты «развёртка»)Шаблон:Sfn.

Последнее определение эвольвенты проясняет следующие свойства эвольвентыШаблон:Sfn:

• касательная в произвольной точке исходной кривой есть нормаль в соответствующей точке эвольвенты;
• всякая ортогональная траектория касательных к исходной кривой есть эвольвента;
• разность радиусов кривизны в двух точках эвольвенты равна длине дуги между соответствующими точками исходной кривой.

У каждой кривой бесконечно много эвольвентШаблон:Sfn, которые параллельны друг другуШаблон:Sfn.

Уравнения эвольвенты

Если линия $L$ задана уравнением $\overline{r}=\overline{r}(s)$ (где $s$ — натуральный параметр), то уравнение её эвольвенты имеет вид

$\overline{\psi }=\overline{r}+(\alpha -s)\dot{\overline{r}}$,

где $\alpha$ — произвольный параметрШаблон:SfnШаблон:Sfn.

Для параметрически заданной кривой уравнение эвольвенты

$X=x-\frac{x^{\prime }\underset{a}{\overset{t}{\int }}\sqrt{x{\text{'}}^2+y{\text{'}}^2}dt}{\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$

$Y=y-\frac{y^{\prime }\underset{a}{\overset{t}{\int }}\sqrt{x{\text{'}}^2+y{\text{'}}^2}dt}{\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$

Примеры эвольвенты

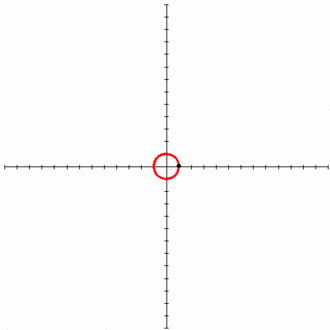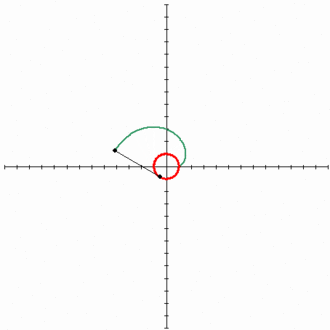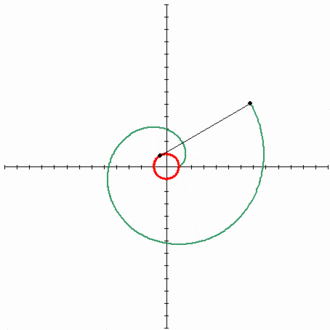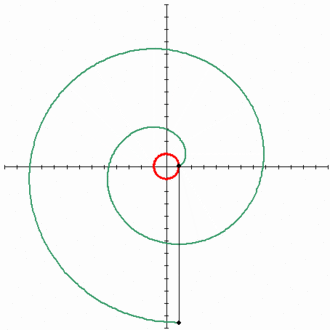
Эвольвентой окружности является спиралевидная кривая. Её параметрические уравнения имеют следующий вид:

$x=r(\cos (t)+t\sin (t)),$

$y=r(\sin (t)-t\cos (t)),$

на комплексной плоскости уравнения упрощаютсяШаблон:Sfn:

$z=r(1-it)e^{it},$

где $t$ — угол, a $r$ — радиус

Эвольвента цепной линии

Применения

• В технике эвольвенту окружности используют:
• как профиль зуба для колёс зубчатой передачи с эвольвентным зацеплением;
• в Шаблон:Iw.

См. также

• Каустика

Литература

• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H