Геометрия инцидентности

Материал из testwiki
Перейти к навигации Перейти к поиску

Геометрия инцидентности — раздел классической геометрии, изучающий структуры инцидентности, например принадлежность точки прямой.

В геометрии объекты, такие как евклидова плоскость, являются сложными объектами, использующими концепции длин, углов, непрерывности, отношения «лежит между» и инцидентности.

Структура инцидентности — это то, что остаётся, если отбросить все понятия, кроме данных о том, какие из изучаемых объектов (например, точки) лежат в других объектах (например, окружностях или прямых). Даже при таких ограничениях некоторые теоремы можно доказать и получить интересные факты относительно такой структуры. Такие фундаментальные результаты остаются верными, если добавить другие концепции для получения более богатой геометрии. Иногда авторы размывают различие между процессом изучения и объектом изучения, так что не удивительно, что некоторые авторы используют для структур инциденций название геометрии инциденций[1].

Структуры инциденций возникают естественным образом и изучались в различных областях математики. Соответственно, существует отличающаяся терминология для описания таких объектов. В теории графов они называются гиперграфами, а в теории комбинаторных схем они называются блок-схемами. Кроме разницы в терминологии, в каждой области подход к изучению объекта отличается, и вопросы к объектам ставятся соответственно дисциплине. Если используется язык геометрии, как это делается в геометрии инциденций, говорят о фигурах. Возможно, однако, перевести результаты с терминологии одной дисциплины на язык другой, но часто это приводит к неуклюжим и запутанным утверждениям, не выглядящим естественным образом для дисциплины. В примерах, приведённых в статье, мы используем только примеры, имеющие геометрическое содержание.

Специальный случай, вызывающий большой интерес, имеет дело с конечным набором точек на евклидовой плоскости и в этом случае речь идёт о числе и типах прямых, которые эти точки определяют. Некоторые результаты этого случая можно распространить на более общие случаи, поскольку здесь рассматриваются только свойства инцидентности.

Структуры инцидентности

Шаблон:Main

Структура инцидентности Шаблон:Math состоит из множества Шаблон:Math, элементы которого называются точками, множества Шаблон:Math , элементы которого называются прямыми, и отношения инцидентности Шаблон:Math между ними, то есть подмножества Шаблон:Math, элементы которого называются флагами [2]. Если Шаблон:Math — флаг, мы говорим, что Шаблон:Math инцидентна Шаблон:Math, или, что Шаблон:Math инцидентна Шаблон:Math (отношение симметрично), и пишем Шаблон:Math. Интуитивно ясно, что точка и прямая находятся в таком отношении тогда и только тогда, когда точка лежит на прямой. Если дана точка Шаблон:Math и прямая Шаблон:Math, которые не образуют флаг, то точка не лежит на прямой и пара Шаблон:Math называется антифлагом.

Расстояние в структуре инциденций

Нет естественного понятия расстояния (метрики) в структуре инциденций. Однако существует комбинаторная метрика в соответствующих графах инциденций (графах Леви), а именно, длина кратчайшего пути между двумя вершинами в этом двудольном графе. Расстояние между двумя объектами структуры инцидентности – двумя точками, двумя прямыми или точкой и прямой – может быть определено как расстояние между двумя соответствующими вершинами в графе инцидентности структуры инцидентности.

Другой путь определения расстояния опять использует понятия теории графов, на этот раз используется граф коллинеарности структуры инцидентности. Вершинами графа коллинеарности являются точки структуры инцидентности и две вершины соединены ребром, если существует прямая, инцидентная обоим точкам. Расстояние между двумя точками структуры инцидентности тогда можно определить как расстояние между ними в графе коллинеарности.

Если расстояние упоминается в контексте структуры инциденций, необходимо указывать, как расстояние определено.

Частично линейные пространства

Наиболее изучаемые структуры инциденций, это структуры, удовлетворяющие некоторым дополнительным свойствам (аксиомам), такие как проективные плоскости, аффинные плоскости, обобщённые многоугольники, частичные геометрии и почти многоугольники. Весьма общие структуры инциденций могут быть получены наложением «мягких» условий, таких как:

Шаблон:Не переведено 5 является структурой инциденций, для которой выполняются следующие аксиомыШаблон:Sfn:

  • Любая пара различных точек определяет максимум одну прямую.
  • Любая прямая содержит по меньшей мере две различные точки.

В частично линейном пространстве также верно, что любая пара различных прямых пересекаются максимум в одной точке. Это утверждение не включается в аксиомы, поскольку легко доказывается из первой аксиомы.

Дальнейшие ограничения задаются условиями регулярности:

RLk: Каждая прямая инцидентна одному и тому же числу точек. Если это число конечно, оно часто обозначается как Шаблон:Math.

RPr: Каждая точка инцидентна одному и тому же числу прямых. Если это число конечно, его часто обозначают как Шаблон:Math.

Из второй аксиомы частично линейного пространства следует, что Шаблон:Math. Ни одно из условий регулярности не вытекает из другого, так что следует принять Шаблон:Math.

Конечное частично линейное пространство, удовлетворяющее обоим условиям регулярности с Шаблон:Math, называется тактической конфигурациейШаблон:Sfn. Некоторые авторы называют такие конфигурации просто конфигурациямиШаблон:Sfn или проективными конфигурациямиШаблон:Sfn. Если тактическая конфигурация имеет Шаблон:Math точек и Шаблон:Math прямых, то, после двойного подсчёта флагов, получается соотношение Шаблон:Math. Обычно используется обозначение Шаблон:Math-конфигурация. В специальном случае, когда Шаблон:Math (а потому, Шаблон:Math), вместо обозначения Шаблон:Math часто пишут просто Шаблон:Math.

Простейшее нетривиальное линейное пространство

Линейное пространство является частично линейным пространством, таким, чтоШаблон:Sfn:

  • Любая пара различных точек определяет в точности одну прямую.

Некоторые авторы добавляют аксиому «невырожденности» (или «нетривиальности») к определению (частичного) линейного пространства, такую как:

  • Существуют по меньшей мере две различные прямые[3].

Аксиома невырожденности позволяет исключить некоторые очень маленькие примеры (в основном те, в которых множества Шаблон:Math или Шаблон:Math состоят менее чем из двух элементов), которые были бы исключениями в общих утверждениях о структурах инцидентности. Альтернативный подход — считать структуры инцидентности, не удовлетворяющие аксиоме невырожденности тривиальными, а удовлетворяющие — нетривиальными.

Любое нетривиальное линейное пространство содержит по меньшей мере три точки и три прямые, так что простейшее нетривиальное линейное пространство — треугольник.

Линейное пространство, имеющее по меньшей мере три точки на каждой прямой, является конфигурацией Сильвестера – Галлаи.

Фундаментальные геометрические примеры

Некоторые из базовых понятий и терминологии возникают из геометрических примеров, особенно из проективных плоскостей и аффинных плоскостей.

Проективные плоскости

Шаблон:Main Проективная плоскость — это линейное пространство, в котором:

  • Любая пара различных прямых пересекаются в точности в одной точке
  • Выполняется условие невырожденности — существует четыре точки, никакие три из которых не коллинеарны.

На проективных плоскостях существует биекция между Шаблон:Math и Шаблон:Math. Если Шаблон:Math является конечным множеством, о проективной плоскости говорят как о конечной проективной плоскости. Порядок конечной проективной плоскости равен Шаблон:Math, то есть на единицу меньше числа точек на прямой. Все известные проективные плоскости имеют порядки, равные степени простого числа. Проективная плоскость порядка Шаблон:Math является конфигурацией Шаблон:Math.

Наименьшая проективная плоскость имеет порядок два и известна как плоскость Фано.

Проективная плоскость порядка 2
плоскость Фано plane

Плоскость Фано

Шаблон:Main

Эта знаменитая геометрия инциденций была разработана итальянским математиком Джино Фано. В его работеШаблон:Sfn по доказательству независимости множества аксиом для проективного n-пространства, которую он разрабатывал [4], он создал конечное трёхмерное пространство с 15 точками, 35 прямыми и 15 плоскостями, в котором каждая прямая содержит только три точки [5]. Плоскости в этом пространстве состоят из семи точек и семи прямых, которые известны как плоскости Фано.

Плоскость Фано не может быть представлена на евклидовой плоскости с использованием только точек и отрезков (т.е. нереализуема). Это следует из теоремы Сильвестра.

Полный четырёхугольник состоит из четырёх точек, никакие три из которых не коллинеарны. На плоскости Фано три точки, не принадлежащие полному четырёхугольнику, являются диагональными точками четырёхугольника и коллинеарны. Это противоречит аксиоме Фано, часто используемой в аксиоматизации евклидовой плоскости, которая утверждает, что три диагональные точки полного четырёхугольника никогда не коллинеарны.

Аффинные плоскости

Шаблон:Main

Аффинная плоскость — это линейное пространство, удовлетворяющее:

О прямых Шаблон:Math и Шаблон:Math в утверждении аксиомы Плейфера говорят как о параллельных. Любая аффинная плоскость может быть единственным образом расширена до проективной плоскости. Порядок конечной аффинной плоскости равен Шаблон:Math, числу точек на прямой. Аффинная плоскость порядка Шаблон:Math является конфигурацией Шаблон:Math.

Аффинная плоскость порядка 3
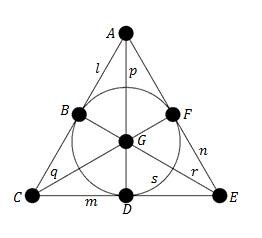
(Конфигурация Гессе)

Конфигурация Гессе

Шаблон:Main

Аффинная плоскость порядка три является конфигурацией Шаблон:Math. Если конфигурация вложена в некоторое объемлющее пространство, её называют конфигурацией Гессе. Конфигурация нереализуема на евклидовой плоскости, но реализуема на комплексной проективной плоскости как девять точек перегиба эллиптической кривой с 12 прямыми, инцидентными тройкам этих точек перегиба.

12 прямых могут быть разбиты на четыре класса, внутри которых прямые попарно не пересекаются. Эти классы называются классами параллельности прямых. Если добавить ещё четыре новые точки, по одной точке в каждый класс параллельности, и считать, что все прямые класса параллельности пересекаются в этой новой точке (таким образом, теперь все прямые теперь пересекаются), и добавить ещё одну прямую, содержащую все четыре новые точки, получим проективную плоскость порядка три, конфигурацию Шаблон:Math. В обратную сторону, начав с проективной плоскости порядка три (такая плоскость единственна) и удалив любую (одну) прямую и все лежащие на ней точки, получим аффинную плоскость порядка три (она тоже единственна).

Удаление одной точки и четырёх прямых, проходящих через неё (но не другие точки на этой прямой), получим конфигурацию Шаблон:Math Мёбиуса — Кантора.

Частичные геометрии

Частичная геометрия pg(2,2,1)

Шаблон:Main

Если задано целое число Шаблон:Math, тактическая конфигурация, удовлетворяющая аксиоме:

называется частичной геометрией. Если существует Шаблон:Math точек на прямой и Шаблон:Math прямых проходят через точку, обозначение этой частичной геометрии — Шаблон:Math.

Если Шаблон:Math, эти частичные геометрии являются обобщёнными четырёхугольниками.

Если Шаблон:Math, конфигурации называются системами Штейнера.

Обобщённые многоугольники

Шаблон:Main

Для Шаблон:Math [6], обобщённый Шаблон:Math-угольник — это частично линейное пространство, граф инцидентности которого Шаблон:Math имеет свойство:

Обобщённый 2-угольник — это структура инцидентности, которая не является частично линейным пространством, состоящая по меньшей мере из двух точек и двух прямых, в которой каждая точка инцидентна каждой прямой. Графом инцидентности обобщённого 2-угольника является полный двудольный граф.

Обобщённый Шаблон:Math-угольник не содержит никаких [[Многоугольник|простых Шаблон:Math-угольников]] для Шаблон:Math и для каждой пары объектов (две точки, две прямые или точка с прямой) существует обычный Шаблон:Math-угольник, содержащий оба объекта.

Обобщённые 3-угольники являются проективными плоскостями. Обобщённые 4-угольники называются обобщёнными четырёхугольниками. По теореме Фейта-Хигмана существует только конечное число обобщённых Шаблон:Math-угольников по меньшей мере с тремя точками на каждой прямой и тремя прямыми, проходящими через каждую прямую, и число Шаблон:Math равно 2, 3, 4, 6 или 8.

Почти многоугольники

Шаблон:Main Для неотрицательных целых Шаблон:Math почти Шаблон:Math-угольник — это структура инцидентности, такая, что:

Почти 0-угольник — это точка, а почти 2-угольник — прямая. Граф коллинеарности почти 2-угольника — полный граф. Почти 4-угольник — это обобщённый четырёхугольник (возможно, вырожденный). Любой конечный обобщённый многоугольник, за исключением проективных плоскостей, является тесным многоугольником. Любой связный двудольный граф является почти многоугольником и любой почти многоугольник, имеющий в точности две точки на каждой прямой, является связным двудольным графом. Также все Шаблон:Не переведено 5 являются почти многоугольниками.

Многие почти многоугольники связаны с Шаблон:Не переведено 5, подобными группам Матьё и группа Янко J2. Более того, обобщённые 2d-угольники, связанные с группами лиева типа, являются специальными случаями почти 2d-угольников.

Плоскости Мёбиуса

Шаблон:Main Абстрактная плоскость Мёбиуса (или инверсная плоскость) — это структура инцидентности, в которой, во избежание возможной путаницы с терминологией классического случая, прямые называют циклами или блоками.

Конкретно: плоскость Мёбиуса — это структура инцидентности точек и циклов, такая, что:

  • Любая тройка различных точек инцидентна в точности одному циклу.
  • Для любого флага Шаблон:Math и любой точки t Шаблон:Math, не инцидентной Шаблон:Math, существует единственный цикл Шаблон:Math с Шаблон:Math и Шаблон:Math}. (Говорят, что циклы касаются Шаблон:Math.)
  • Любой цикл имеет по меньшей мере три точки и существует по меньшей мере один цикл.

Структура инцидентности, полученная из любой точки Шаблон:Math плоскости Мёбиуса путём выбора в качестве точек всех точек, отличных от Шаблон:Math, а в качестве прямых выбора только тех циклов, которые содержат Шаблон:Math (с удалённой Шаблон:Math), является аффинной плоскостью. Эта структура называется остатком Шаблон:Math в теории схем.

Конечная плоскость Мёбиуса порядка Шаблон:Math — это тактическая конфигурация с Шаблон:Math точками в каждом цикле, которая является 3-дизайном, блок-схемой Шаблон:Math.

Теоремы инцидентности на евклидовой плоскости

Теорема Сильвестра

Шаблон:Main Вопрос, поставленный Д.Д. Сильвестером в 1893 и, наконец, доказанной Шаблон:Не переведено 5, касается инцидентности конечного числа точек в евклидовой плоскости.

Теорема (Сильвестр — Галлаи): Точки конечного множества точек на евклидовой плоскости либо коллинеарны, либо существует прямая, инцидентная в точности двум точкам.

Прямая, содержащая в точности две точки, называется в этом контексте обычной прямой. Сильвестр, возможно, пришёл к этому вопросу, когда обдумывал вложимость конфигурации Гессе.

Теорема де Брёйна — Эрдёша

Шаблон:Main Связанный результат — теорема де Брёйна — Эрдёша. Николас де Брёйн и Пал Эрдёш доказали результат в более общих условиях проективной плоскости, но результат остаётся верным на евклидовой плоскости. Теорема гласит:[7]

На проективной плоскости любое множество Шаблон:Math неколлинеарных точек определяет по меньшей мере Шаблон:Math различных прямых.

Как указали авторы, поскольку их доказательство было комбинаторным, результат выполняется в более сильных условиях, фактически в любой геометрии инцидентности. Они также упомянули, что версия для евклидовой плоскости может быть доказана из теоремы Сильвестера — Галлаи с помощью индукции.

Теорема Семереди – Троттера

Шаблон:Main

Граница числа флагов, определённая конечным множеством точек и прямых, задаётся теоремой:

Теорема (Семереди – Троттер): Если задано Шаблон:Math точек и Шаблон:Math прямых на плоскости, число флагов (пар инцидентности точка-прямая) равно:

O(n23m23+n+m),

И эта граница не может быть улучшена.

Этот результат можно использовать для доказательства теоремы Бека.

Теорема Бека

Шаблон:Main

Теорема Бека утверждает, что конечные наборы точек на плоскости распадаются на два крайних случая — в одних наборах все точки лежат на одной прямой, а в других нужно большое число прямых для соединения всех точек.

Теорема утверждает, что существуют положительные константы Шаблон:Math, такие, что, если заданы Шаблон:Math точек на плоскости, по меньшей мере одно из следующих утверждение верно:

  1. Существует прямая, содержащая по меньшей мере n/C точек.
  2. Существует по меньшей мере n2/K прямых, каждая из которых содержит по меньшей мере две точки.

В исходных доказательствах Бека Шаблон:Math равно 100, а Шаблон:Math является неопределённой константой. Оптимальные значения Шаблон:Math и Шаблон:Math неизвестны.

Дальнейшие примеры

См. также

Примечания

Шаблон:Примечания

Литература

Ссылки

Шаблон:Rq

  1. ↑ Так, например, делает Л. Сторме в главе о конечной геометрии в книге Шаблон:Harv
  2. ↑ Технически, это структура инцидентности ранга 2, где ранг относится к числу типов объектов рассмотрения (здесь — точки и прямые). Структуры более высоких рангов также изучаются, но некоторые авторы ограничивают себя рангом 2 и мы будем делать то же самое.
  3. ↑ Существует несколько альтернативных аксиом такой «нетривиальности». Аксиома может быть заменена на «существует три точки, не лежащие на одной прямой», как в книге Баттена и Бойтельшпахера Шаблон:Harv. Есть другие варианты, но во всех должно присутствовать утверждение существования, которое исключает слишком простые случаи.
  4. ↑ Шаблон:Harvnb
  5. ↑ Шаблон:Harvnb, Finite Geometries? an AMS Featured Column
  6. ↑ Использование Шаблон:Math в имени является стандартным и не следует путать это число с числом точек в конфигурации.
  7. ↑ Weisstein, Eric W. Шаблон:Wayback, "de Bruijn–Erdős Theorem" Шаблон:Wayback на MathWorld Шаблон:Архивировано
Источник — https://ru.wiki.beta.math.wmflabs.org/w/index.php?title=Геометрия_инцидентности&oldid=17684