Цилиндрическая система координат

Точка в цилиндрических координатах.

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой $z$), которая задаёт высоту точки над плоскостью.

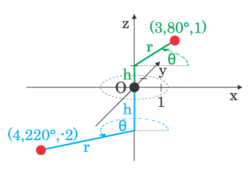
Точка $P$ даётся как $(\rho ,\phi ,z)$. В терминах прямоугольной системы координат:

• $\rho ⩾0$ — расстояние от $O$ до $P^{\prime }$, ортогональной проекции точки $P$ на плоскость $XY$. Или то же самое, что расстояние от $P$ до оси $Z$.
• $0⩽\phi <360^{\circ }$ — угол между осью $X$ и отрезком $O{P}^{\prime }$.
• $z$ равна аппликате точки $P$.

При использовании в физических науках и технике международный стандарт ISO 31-11 рекомендует использовать обозначения $(\rho ,\phi ,z)$.

Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось $Z$ взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр (цилиндрическая поверхность) в прямоугольных координатах имеет уравнение $x^2+y^2=c^2$, а в цилиндрических — очень простое уравнение $\rho =c$. Отсюда и идёт для данной системы координат имя «цилиндрическая».

Переход к другим системам координат

2 точки в цилиндрических координатах.

Поскольку цилиндрическая система координат — только одна из многих трёхмерных систем координат, существуют законы преобразования координат между цилиндрической системой координат и другими системами.

Декартова система координат

Шаблон:Main Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями:

$\{\begin{array}{c}{\overrightarrow{e}}_{\rho }=\cos \phi {\overrightarrow{e}}_x+\sin \phi {\overrightarrow{e}}_y,\\ {\overrightarrow{e}}_{\phi }=-\sin \phi {\overrightarrow{e}}_x+\cos \phi {\overrightarrow{e}}_y,\\ {\overrightarrow{e}}_z={\overrightarrow{e}}_z,\end{array}$

и образуют правую тройку:

$\{\begin{array}{c}{\overrightarrow{e}}_{\rho }\times {\overrightarrow{e}}_{\phi }={\overrightarrow{e}}_z,\\ {\overrightarrow{e}}_z\times {\overrightarrow{e}}_{\rho }={\overrightarrow{e}}_{\phi },\\ {\overrightarrow{e}}_{\phi }\times {\overrightarrow{e}}_z={\overrightarrow{e}}_{\rho }.\end{array}$

Обратные соотношения имеют вид:

$\{\begin{array}{c}{\overrightarrow{e}}_x=\cos \phi {\overrightarrow{e}}_{\rho }-\sin \phi {\overrightarrow{e}}_{\phi },\\ {\overrightarrow{e}}_y=\sin \phi {\overrightarrow{e}}_{\rho }+\cos \phi {\overrightarrow{e}}_{\phi },\\ {\overrightarrow{e}}_z={\overrightarrow{e}}_z.\end{array}$

Закон преобразования координат от цилиндрических к декартовым:

$\{\begin{array}{c}x=\rho \cos \phi ,\\ y=\rho \sin \phi ,\\ z=z.\end{array}$

Закон преобразования координат от декартовых к цилиндрическим:

$\{\begin{array}{c}\rho =\sqrt{x^2+y^2},\\ \phi =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{g}\left(\frac{y}{x}\right),\\ z=z.\end{array}$

Якобиан равен:

$J=\rho .$

Дифференциальные характеристики

Цилиндрические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

$g_{ij}=\left(\begin{array}{ccc}1& 0& 0\\ 0& {\rho }^2& 0\\ 0& 0& 1\end{array}\right),g^{ij}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1/{\rho }^2& 0\\ 0& 0& 1\end{array}\right).$

• Квадрат дифференциала длины кривой

$d{s}^2=d{\rho }^2+{\rho }^{2}d{\phi }^2+d{z}^2.$

• Коэффициенты Ламэ имеют вид:

$H_{\rho }=1,H_{\phi }=\rho ,H_z=1.$

• Символы Кристоффеля $\{\rho ,\phi ,z\}$:

${\mathrm{\Gamma }}_{22}^1=-\rho ,{\mathrm{\Gamma }}_{21}^2={\mathrm{\Gamma }}_{12}^2=\frac{1}{\rho }.$

Остальные равны нулю.

Дифференциальные операторы

Шаблон:Main Градиент в цилиндрической системе координат:

$\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\psi ={\overrightarrow{e}}_{\rho }\frac{\partial \psi }{\partial \rho }+{\overrightarrow{e}}_{\phi }\frac{1}{\rho }\frac{\partial \psi }{\partial \phi }+{\overrightarrow{e}}_z\frac{\partial \psi }{\partial z}.$

Лапласиан в цилиндрической системе координат:

$\mathrm{\Delta }\psi =\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial \psi }{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2\psi }{\partial {\phi }^2}+\frac{{\partial }^2\psi }{\partial z^2}.$

Дивергенция в цилиндрической системе координат:

$\mathrm{d}\mathrm{i}\mathrm{v}\overrightarrow{a}=\frac{1}{\rho }\frac{\partial \rho a_{\rho }}{\partial \rho }+\frac{1}{\rho }\frac{\partial a_{\phi }}{\partial \phi }+\frac{\partial a_z}{\partial z}.$

Ротор в цилиндрической системе координат:

$\mathrm{r}\mathrm{o}\mathrm{t}\overrightarrow{a}=\mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{ccc}\frac{1}{\rho }{\overrightarrow{e}}_{\rho }& {\overrightarrow{e}}_{\phi }& \frac{1}{\rho }{\overrightarrow{e}}_z\\ \frac{\partial }{\partial \rho }& \frac{\partial }{\partial \phi }& \frac{\partial }{\partial z}\\ a_{\rho }& \rho a_{\phi }& a_z\end{array}\right)={\overrightarrow{e}}_{\rho }(\frac{1}{\rho }\frac{\partial a_z}{\partial \phi }-\frac{\partial a_{\phi }}{\partial z})+{\overrightarrow{e}}_{\phi }(\frac{\partial a_{\rho }}{\partial z}-\frac{\partial a_z}{\partial \rho })+{\overrightarrow{e}}_z(\frac{1}{\rho }\frac{\partial \rho a_{\phi }}{\partial \rho }-\frac{1}{\rho }\frac{\partial a_{\rho }}{\partial \phi }).$

Выражения для радиус-вектора, скорости и ускорения в цилиндрических координатах

Шаблон:Проще $r(t)=\rho {\overrightarrow{e}}_{\rho }+z{\overrightarrow{e}}_z$

$\dot{r}(t)=\dot{\rho }{\overrightarrow{e}}_{\rho }+\rho \dot{\phi }{\overrightarrow{e}}_{\phi }+\dot{z}{\overrightarrow{e}}_z$

$\ddot{r}(t)=(\ddot{\rho }-\rho {\dot{\phi }}^2){\overrightarrow{e}}_{\rho }+(2\dot{\rho }\dot{\phi }+\ddot{\phi }\rho ){\overrightarrow{e}}_{\phi }+\ddot{z}{\overrightarrow{e}}_z$

См. также

• Углы Эйлера
• Цилиндрические шахматы

Литература

• Халилов В.Р., Чижов Г.А., Динамика классических систем: Учеб. пособие. — М.: Изд-во МГУ, 1993. — 352 с.