Улитка Паскаля

Семь форм улиток Паскаля как конхоиды чёрной окружности с полюсом (0, 0): $r(\phi )=2a\cos \phi +l.$ Из них красная — с параболической точкой распрямления, зелёная — кардиоида, синяя — трисектриса

Страница книги Дюрера 1525 года с линией паука (Spinnenlinie)

Ули́тка Паска́ля (Шаблон:Lang-enШаблон:SfnШаблон:Sfn, от лат. limax — улитка; Шаблон:Lang-enШаблон:SfnШаблон:Sfn; snail curveШаблон:Sfn) ― конхоида окружности с полюсом на этой окружностиШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn.

Синонимы: улиткаШаблон:SfnШаблон:Sfn (Шаблон:Lang-enШаблон:SfnШаблон:Sfn); конхоида кругаШаблон:Sfn.

Обычно представляется следующим уравнением конхоиды окружности в полярной системе координат при допуске отрицательных радиус-векторовШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn:

$r(\phi )=2a\cos \phi +l,$

где $a$ — радиус базовой окружности конхоиды; $l$ — приращение радиус-вектора окружности, проведённого из полюса конхоиды на окружности.

Относится к плоским алгебраически кривым 4-го порядкаШаблон:SfnШаблон:SfnШаблон:Sfn.

Улитка Паскаля — это кривая, обладающая следующими простыми свойствамиШаблон:Sfn:

• ограниченная и замкнутая;
• связная только для кардиоиды и улитки с петлёй, остальные кривые имеют изолированную точку;
• имеет одну особую точку — двойную: точку самопересечения, касп или изолированную в зависимости от параметров;
• имеет одну ось симметрии.

Названа по имени французского учёного Этьена Паскаля (отца Блеза Паскаля), рассмотревшего её в первой половине XVII векаШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn. Улитка Паскаля изучалась Альбрехтом Дюрером в 1525 году под названием арахна (линия паука) (Шаблон:Lang-en; Шаблон:Lang-deШаблон:Sfn; Шаблон:Lang-frШаблон:Sfn), Этьеном Паскалем в 1630 году и Жилем Робервалем, который и назвал кривую «улиткой Паскаля» в 1650 годуШаблон:SfnШаблон:SfnШаблон:Sfn.

Определения улитки Паскаля

Самые распространённые определение и уравнение

Ули́тка Паска́ля (Шаблон:Lang-en; snail curveШаблон:Sfn) ― конхоида окружности с полюсом на этой окружностиШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn, обычно задаваемая следующим уравнением в полярной системе координат при допуске отрицательных радиус-векторовШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn:

$r(\phi )=2a\cos \phi +l,$

где $a$ — радиус базовой окружности $r(\phi )=2a\cos \phi$ конхоиды; $l$ — приращение радиус-вектора окружности, проведённого из полюса конхоиды.

Базовая окружность $r(\phi )=2a\cos \phi$ улитки Паскаля называется также её директрисойШаблон:Sfn, а приращение $l$ радиус-вектора окружности — её модулемШаблон:Sfn.

Улитка Паскаля — это кривая, обладающая следующими основными свойствамиШаблон:Sfn:

• ограниченная и замкнутая;
• связная только для кардиоиды и улитки с петлёй, остальные кривые имеют изолированную точку;
• имеет одну особую точку — двойную: точку самопересечения, касп или изолированную в зависимости от параметров;
• имеет одну ось симметрии.

Обычное уравнение улитки Паскаля в полярой системе координат

$r=2a\cos \phi +l,$

может быть записано по-другому:

• в сокращённой формеШаблон:SfnШаблон:SfnШаблон:Sfn:

$r=d\cos \phi +l,$

где $d$ — диаметр базовой окружности конхоиды;

• в размерно-безразмерной формеШаблон:Sfn:

$r=l(e\cos \phi +1),$

где $le=2a$ — диаметр базовой окружности конхоиды; $e=\frac{2a}{l}$ — безразмерный параметр;

• в безразмерной формеШаблон:Sfn:

$\rho =2\cos \phi +ϵ,$

где $\rho =\frac{r}{a},$ $ϵ=\frac{l}{a}$ — безразмерные параметры.

Все уравнения, рассмотренные выше, имеют горизонтальную ось симметрии (совпадающую с осью абсцисс) и как полюс коноиды, так и особые точки, расположенные слева. Но особые точки можно расположить на графике и справа, записав уравнение улитки Паскаля в следующей форме:

$r=-2a\cos \phi +l,$

У всех уравнений, рассмотренные выше, ось симметрии совпадает с осью абсцисс. У следующих уравнений ось симметрии улитки Паскаля совпадает с осью ординатШаблон:Sfn:

• полюс коноиды и особые точки расположены вверху:

$r=-2a\sin \phi +l;$

• полюс коноиды и особые точки расположены внизу:

$r=2a\sin \phi +l.$

Вывод уравнения и геометрическое построение

Геометрическое построение красной точки улитки Паскаля (трисектрисы, $l=a$)

Детализируем определение улитки Паскаля, расшифровав понятие конхоиды:

ули́тка Паска́ля — геометрическое место концов радиус-векторов, проведённых из фиксированной точки на окружности радиуса $a$ ко всем точкам окружности, причём эти радиус-векторы увеличены (одна ветвь) или уменьшены (другая ветвь) на постоянную величину $l$Шаблон:Sfn.

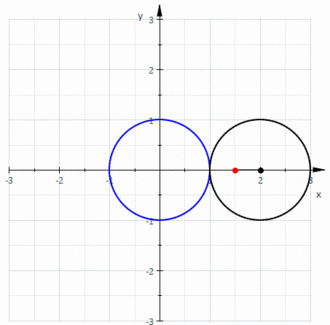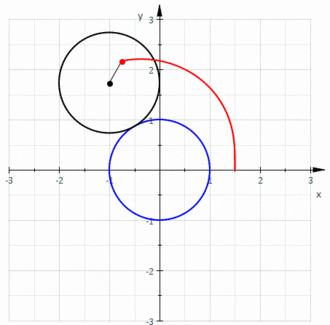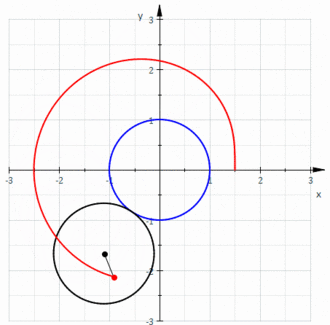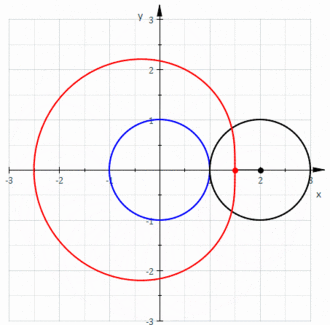
Получим уравнение улитки Паскаля в полярной системе координат. Для этого (см. рисунок справа)Шаблон:Sfn:

• поместим полюс конхоиды, расположенный на базовой окружности, в начало полярной системы координат;
• расположим диаметр базовой окружности на полярной оси справа от начала координат;
• радиус-вектор из определения равен

$r(\phi )=2a\cos \phi ;$

• увеличенный на $l$ радиус-вектор из определения равен

$r(\phi )=2a\cos \phi +l,$

и последнее уравнение есть уравнение первой ветви улитки Паскаля при $l>0$, второй ветви — при $l<0$Шаблон:Sfn.

Поскольку

$r(\phi )=2a\cos \phi +l=2a\cos (\pi +\phi )-l,$

то обе ветви улитки Паскаля образуют одну замкнутую непрерывную кривую, причём каждая из ветвей рисуется дважды, первый раз при $l>0$, второй раз при $l<0${Шаблон:Sfn.

При первом проходе при $l>0$ при повороте радиус-вектора от $0^{\circ }$ до $90^{\circ }$ конец увеличенного радиус-вектора описывает в первом квадранте верхнюю половину первой ветви улитки Паскаля, как показано на первом рисунке внизу на первом подрисунке слева. При дальнейшем повороте радиус-вектора от $90^{\circ }$ до $180^{\circ }$ получается первая половина второй ветви улитки Паскаля, при этом радиус-вектор отрицательный, но его увеличение откладывается от его конца всё равно в положительном направлении, как показано на первом рисунке внизу на втором подрисунке слева. Аналогично рисуется вторая половина улитки Паскаля, как показано на первом рисунке внизу на третьем и четвёртом подрисунках слева. Второй проход при $l<0$ происходит аналогично, как показано на втором рисунке внизуШаблон:Sfn{Шаблон:Sfn.

Конхоидное преобразование улитки Паскаля (не окружности)

$r(\phi )=2a\cos \phi +l$

с полюсом этой же улитки и с модулем $l^{\prime }$ есть снова улитка Паскаля

$r(\phi )=2a\cos \phi +l\pm l^{\prime }$,

но в этом случае ветви всегда будут разные, причём если $l^{\prime }=l$, то вторая ветвь будет окружностью.

• Ветви улитки Паскаля (трисектрисы) при положительном модуле для квадрантов плоскости
• 
  Первая ветвь. $0^{\circ }⩽\phi ⩽90^{\circ }$
• 
  Вторая ветвь. $90^{\circ }⩽\phi ⩽180^{\circ }$
• 
  Вторая ветвь. $180^{\circ }⩽\phi ⩽270^{\circ }$
• 
  Первая ветвь. $270^{\circ }⩽\phi ⩽360^{\circ }$

• Ветви улитки Паскаля (трисектрисы) при отрицательном модуле для квадрантов плоскости
• 
  Вторая ветвь. $0^{\circ }⩽\phi ⩽90^{\circ }$
• 
  Первая ветвь. $90^{\circ }⩽\phi ⩽180^{\circ }$
• 
  Первая ветвь. $180^{\circ }⩽\phi ⩽270^{\circ }$
• 
  Вторая ветвь. $270^{\circ }⩽\phi ⩽360^{\circ }$

Уравнение в других координатных системах

Для перевода уравнения кривой из полярной системы координат $(r,\phi )$ в декартовую $(x,y)$ (и обратно) используют соотношения

$x=r\cos \phi ,$ $y=r\sin \phi ,$ $x^2+y^2=r^2,$

поэтому декартовое уравнение улитки Паскаля будет следующимШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn:

$r(\phi )=2a\cos \phi +l,$

$x^2+y^2=2ax+l\sqrt{x^2+y^2},$

$(x^2+y^2-2ax{)}^2=l^2(x^2+y^2).$

Используя те же формулы

$x=r\cos \phi ,$ $y=r\sin \phi ,$

параметрические декартовые уравнения улитки Паскаля можно также получить из полярного уравненияШаблон:SfnШаблон:Sfn:

$r(\phi )=2a\cos \phi +l,$

$x=2a{\cos }^{2}t+l\cos t=a\cos 2t+l\cos t+a,$

$y=2a\cos t\sin t+l\sin t=a\sin 2t+l\sin t.$

Декартовы параметрические уравнения улитки Паскаля могут быть и следующиеШаблон:Sfn:

$x=\frac{(1-t^2)(l+2a+(l-2a)t^2)}{(1+t^2{)}^2},$

$y=\frac{2t(l+2a+(l-2a)t^2)}{(1+t^2{)}^2}.$

Комплексное параметрическое уравнение улитки Паскаля так же получается из полярного уравнения с использованием соотношений

$z(\phi )=r(\phi )e^{i\phi },\cos \phi =\frac{1}{2}(e^{i\phi }+e^{-i\phi })$

и имеет следующий видШаблон:SfnШаблон:Sfn:

$r(\phi )=2a\cos \phi +l,$

$r{e}^{it}=(2a\cos \phi +l)e^{it},$

$z=a(1+e^{2it})+l{e}^{it}.$

В случае $l=a$ улитка Паскаля также называется трисектри́са. Такое название она получила из-за того, что если на плоскости задана эта улитка Паскаля, то трисекцию угла можно построить с помощью циркуля и линейкиШаблон:Sfn. Уравнение трисектрисыШаблон:Sfn:

$z=a(1+e^{it}+e^{2it})=a+a{e}^{\frac{3it}{2}}(e^{\frac{it}{2}}+e^{\frac{-it}{2}})=a+2a{e}^{\frac{3it}{2}}\cos \frac{t}{2},$

в полярных координатах:

$r=2a\cos \frac{\phi }{3}.$

Виды улиток Паскаля

Примечательные точки улитки Паскаля

Существуют три вида улиток Паскаля: гиперболические, параболические (кардиоиды) и эллиптическиеШаблон:Sfn. Будем использовать уравнение улитки Паскаля

$r(\phi )=2a\cos \phi +l.$

Гиперболические улитки Паскаля $r(\phi )=2a\cos \phi +l,$ $l<2a$ с примечательными точками и касателными в точках самопересечения

Две касательные прямые всех улиток Паскаля в особой точке — полюсе конхоиды, он же начало координат $r=0,$ — имеют следующее уравнениеШаблон:Sfn:

$4a^2{\cos }^2\phi -l^2=0,$

поэтому (см. рисунки справа):

• если $l<2a,$ то касательные действительные, и особая точка — точка самопересечения параболической улитки Паскаля;
• если $l=2a,$ то касательные совпадают с осью абсцисс, и особая точка — касп кардиоиды;
• если $l>2a,$ то касательные мнимые, и особая точка — изолированная эллиптической улитки Паскаля.

Вершины всех видов улиток Паскаля, если они есть, удовлетворяют следующему уравнению, полученному приравниванием нулю производной

${\kappa }^{\prime }(\phi )=\frac{12a^{2}l\sin \phi (l\cos \phi +2a)}{(\sqrt{4al\cos \phi +4a^2+l^2}{)}^5}$

кривизныШаблон:Sfn

$\kappa (\phi )=\frac{6al\cos \phi +8a^2+l^2}{(\sqrt{4al\cos \phi +4a^2+l^2}{)}^3},$

то есть это необходимое условие быть вершиной (но не достаточное)Шаблон:Sfn:

$\sin \phi (l\cos \phi +2a)=0.$

Эллиптические улитки Паскаля $r(\phi )=2a\cos \phi +l,$ $l>2a$ с примечательными точками

Последнее уравнение есть совокупность уравнений

$[\begin{array}{c}\sin \phi =0,\\ l\cos \phi +2a=0,\end{array}$

откуда вершины, если они есть, имеют координаты (см. рисунки справа)

$[\begin{array}{c}\sin \phi =0,r=l\pm 2a,\\ \cos \phi =-\frac{2a}{l},r=l-\frac{4a^2}{l}\end{array}$

и лежат на прямой и циссоиде Диокла (см. рисунок справа)

$[\begin{array}{c}\sin \phi =0,\\ r=2a(\cos \phi -\frac{1}{\cos \phi })=-\frac{2a{\sin }^2\phi }{\cos \phi }.\end{array}$

Грушевидная квартика, составленная из точек перегиба эллиптических улиток Паскаля $r(\phi )=2a\cos \phi +l,$ $l>2a$

Точки перегиба эллиптических улиток Паскаля, если они есть, удовлетворяют следующему уравнению, полученному приравниванием нулю кривизны, то есть это необходимое условие быть точкой перегиба (но не достаточное)Шаблон:Sfn:

$6al\cos \phi +l^2+8a^2=0,$

откуда точки перегиба, если они есть, имеют координаты (см. рисунки справа)

$\cos \phi =-\frac{l^2+8a^2}{6al},$

$r=l-\frac{l^2+8a^2}{3l}=\frac{2l^2-8a^2}{3l}.$

и лежат на обобщённой грушевидной квартикеШаблон:Sfn (см. рисунок справа)

$r^2+2ar\cos \phi -8a^2{\cos }^2\phi +8a^2=0,$

или

$r^2+2ar\cos \phi +8a^2{\sin }^2\phi =0,$

или

$(r+a\cos \phi {)}^2+a^2(8{\sin }^2\phi -{\cos }^2\phi )=0.$

Гиперболическая улитка Паскаля

Трисектриса $r(\phi )=a(2\cos \phi +1),$ $a=2$ с точкой самопересечения и двумя вершинами

Гиперболическая улитка (Шаблон:Lang-en) — улитка Паскаля, у которой параметры отвечают следующему неравенствуШаблон:Sfn:

$l<2a.$

Синоним:

• улитка с петлёй (Шаблон:Lang-en)Шаблон:Sfn.

Частные случаиШаблон:Sfn:

• улитка Паскаля вырождается в окружность радиуса $a$ при

$l=0,$

то есть уравнение окружности

$r(\phi )=2a\cos \phi ;$

• улитка Паскаля есть трисектриса (Шаблон:Lang-en; Шаблон:Lang-enШаблон:SfnШаблон:SfnШаблон:Sfn) при

$l=a,$

то есть её уравнение

$r(\phi )=a(2\cos \phi +1).$

Перечислим примечательные точки трисектрисы как типичного представителя улитки с петлёй (см. рисунок справа)Шаблон:Sfn:

• трисектриса имеет точку самопересечения в начале координат $r=0;$
• радиальные координаты кандидатов в точки перегиба

$\cos \phi =-\frac{3}{2}<-1,$ $r=\frac{2l^2-8a^2}{3l}=-2a,$

поэтому точек перегиба нет;

• из вершин попадают на кардиоиду и не попадают на точку самопересечения только две точки

$\phi =0,r=3a$ и $\phi =\pi ,r=-a.$

Параболическая улитка Паскаля

Кардиоида $r(\phi )=2a(\cos \phi +1),$ $a=2$ с каспом и вершиной

Параболическая улитка (Шаблон:Lang-en) — улитка Паскаля, у которой параметры отвечают следующему равенствуШаблон:Sfn:

$l=2a,$

то есть её уравнение

$r(\phi )=2a(\cos \phi +1).$

Синонимы:

• улитка с каспом (Шаблон:Lang-en)Шаблон:Sfn,
• кардиоида (Шаблон:Lang-en)Шаблон:Sfn,

Перечислим примечательные точки кардиоиды (см. рисунок справа)Шаблон:Sfn:

• кардиоида имеет касп в начале координат $r=0;$
• радиальная координата кандидата в точки перегиба

$r=\frac{2l^2-8a^2}{3l}=0,$

поэтому точек перегиба нет, точка $r=0$ — это касп;

• из вершин попадает на кардиоиду и не попадает на касп только точка

$\phi =0,r=4a.$

Эллиптическая улитка Паскаля

Эллиптическая улитка (Шаблон:Lang-en) — улитка Паскаля, у которой параметры отвечают следующему неравенствуШаблон:Sfn:

$l>2a.$

Синонимы:

• улитка с изолированной точкой (Шаблон:Lang-en)Шаблон:Sfn;
• обычная улитка (Шаблон:Lang-en)Шаблон:Sfn.

Частные случаиШаблон:Sfn:

• улитка в форме фасолины (Шаблон:Lang-en) при

$2a<l<4a;$

• улитка с параболической точкой распрямления (Шаблон:Lang-en) при

$l=4a;$

• выпуклая улитка (Шаблон:Lang-en) при

$4a<l<\mathrm{\infty };$

• улитка Паскаля вырождается в окружность бесконечного радиуса при

$l\to \mathrm{\infty }.$

Перечислим примечательные точки представителя улитки в форме фасолины с $l=4a$ (см. рисунок ниже)Шаблон:Sfn:

• улитка в форме фасолины имеет изолированную точку в начале координат $r=0;$
• из точек перегиба присутствуют все две точки

$\cos \phi =-\frac{17}{18},$ $r=\frac{10}{9}a;$

• из вершин попадают на улитку в форме фасолины все четыре точки

$[\begin{array}{c}\phi =0,r=5a\text{и}\phi =\pi ,r=a,\\ \cos \phi =-\frac{2}{3},r=\frac{5}{3}a.\end{array}$

Перечислим примечательные точки представителя улитки с параболической точкой распрямления с $l=3a$ (см. рисунок ниже)Шаблон:Sfn:

• улитка с параболической точкой распрямления имеет изолированную точку в начале координат $r=0;$
• две точки перегиба сливаются в одну параболическую точку распрямления (слияние и исчезновение точек перегиба и вершин типично для кривых, при слиянии «качество» точки меняется в более «сильную» сторону)

$\cos \phi =-1,$ $r=2a;$

• из вершин попадают на улитку с параболической точкой распрямления все четыре точки, но одна попадает на параболическую точку распрямления

$[\begin{array}{c}\phi =0,r=6a\text{и}\phi =\pi ,r=2a,\\ \cos \phi =-\frac{1}{2},r=3a.\end{array}$

Перечислим примечательные точки представителя выпуклой улитки с $l=5a$ (см. рисунок ниже)Шаблон:Sfn:

• выпуклая улитка имеет изолированную точку в начале координат $r=0;$
• радиальные координаты кандидатов в точки перегиба

$\cos \phi =-\frac{11}{10}<-1,$ $r=\frac{42}{15}a,$

поэтому точек перегиба нет;

• из вершин попадают на выпуклую улитку все четыре точки

$[\begin{array}{c}\phi =0,r=7a\text{и}\phi =\pi ,r=3a,\\ \cos \phi =-\frac{2}{5},r=\frac{21}{5}a.\end{array}$

• Формы эллиптической улитки Паскаля
• 
  Улитка в форме фасолины $r(\phi )=a(2\cos \phi +3),$ $a=2$ с изолированной точкой, двумя точками перегиба и четырьмя вершинами
• 
  Улитка с параболической точкой распрямления $r(\phi )=2a(\cos \phi +2),$ $a=2$ с изолированной точкой, параболической точкой распрямления и тремя вершинами
• 
  Выпуклая улитка $r(\phi )=a(2\cos \phi +5),$ $a=2$ с изолированной точкой и четырьмя вершинами

Свойства

Анимация подеры окружности — улитки Паскаля

Анимация эпитрохоиды окружности — улитки Паскаля

• Улитка Паскаля является подерой окружности относительно любой точки, кроме центра окружности.
• Улитка Паскаля является частным случаем Декартова овала.
• Улитка Паскаля является частным случаем эпитрохоиды.
• Улитка Паскаля является примером эквихордной кривой.
• Длина дуги выражается эллиптическим интегралом 2-го рода.
• Площадь, ограниченная улиткой Паскаля:

  $S=\frac{\pi a^2}{2}+\pi {\ell }^2.$

При $a>\ell$ площадь внутренней петли при вычислении по этой формуле считается дважды.

Применение в технике

Эксцентрик в виде эллиптической улитки Паскаля

Стержень, скользящий по эксцентрику с профилем эллиптической улитки Паскаля, совершает гармонические колебания. В самом деле, пусть $S$ — это поступательное движение точки $M$соприкосновения стрежня и эксцентрика (см. рисунок справа), тогда

$S=\rho =2r\cos \omega t+l,$

где $\omega$ — угловая скорость эксцентрика, а

$v=S^{\prime }=-2r\omega \sin \omega t$ —

скорость возвратно-поступательного движения стержня, которая изменяется без скачков, совершая гармонические колебанияШаблон:Sfn.

Такие изменения без скачков скорости движения стержня по эксцентрику, очерченному по улитке Паскаля, существенно выгоднее, чем движение стержня по эксцентрику, очерченному по спирали Архимеда. Последнее по причине своей постоянной скорости $v$ в конце каждого хода испытывает удары, при которых скорость скачком меняется с $v$ на $-v$. Такие удары влекут быстрое изнашивание этого механизмаШаблон:Sfn.

В семафоре на железной дороге одна из частей механизма очерчена по улитке Паскаля. По этой причине скорость поднятия или опускания крыла семафораШаблон:Sfn:

• минимальна в начале поднятия или опускания;
• достигает максимального значения в середине хода.

Такое поведение скорости движения крыла семафораШаблон:Sfn:

• обеспечивает её плавность с незначительными начальными и конечными толчками;
• способствует преодолению сил инерции и трения, особенно сильных в начале работы привода крыла.

Источники

• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H
• Шаблон:H

Литература

• Limacon of Pascal at The MacTutor History of Mathematics
• Limacon of Pascal at Visual Dictionary of Special Plane Curves
• A red limaçon of Pascal - построение в Sage Math с использованием библиотеки Matplotlib