Подера
Поде́ра (Шаблон:Lang-fr, от др.-греч. πούς, род. пад. ποδός — ногаШаблон:SfnШаблон:Sfn, то есть стопа перпендикуляра; Шаблон:Lang-en) кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривойШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn.
Устаревший термин подэ́раШаблон:SfnШаблон:SfnШаблон:Sfn, или подэ́рная крива́яШаблон:Sfn.
В некоторых математических текстах вместо русского термина «подера» используется калька с английского «педаль»Шаблон:SfnШаблон:Sfn.
Например, подера окружности относительно точки, лежащей не в центре окружности, — это улитка ПаскаляШаблон:SfnШаблон:Sfn.
Подера кривой есть инверсия полярного преобразования кривой, полюсы которых совпадают с полюсом подерыШаблон:Sfn.
Впервые подера рассмотрена 30 июня 1718 года Колином Маклореном (Шаблон:Lang-en), профессором математики из Абердина, в журнале Философские труды Королевского общества (Шаблон:Lang-en) в статье на латинском языке «III. Трактат о построении и измерении кривых, где большинство бесконечных серий кривых сводятся либо к прямым линиям, либо к более простым кривым. Автор Колин Маклорен, профессор математики в Шаблон:Iw Шаблон:Iw» (Шаблон:Lang-la)Шаблон:SfnШаблон:SfnШаблон:Sfn.
Определения
Определения подеры и антиподеры на плоскости
Поде́ра, или (первая) позитивная подераШаблон:SfnШаблон:Sfn, или подошвенная криваяШаблон:Sfn (Шаблон:Lang-en), кривой — некоторая кривая, составленная из оснований перпендикуляров, опущенных из фиксированной точки, которая называется полюсомШаблон:SfnШаблон:SfnШаблон:Sfn, или центромШаблон:Sfn, или точкой подерыШаблон:SfnШаблон:Sfn, на касательные к исходной кривойШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:SfnШаблон:Sfn. Подера кривой порядка , , имеет порядок Шаблон:Sfn.
Устаревший термин подэ́раШаблон:SfnШаблон:SfnШаблон:Sfn, или подэ́рная крива́яШаблон:Sfn.
В некоторых математических текстах вместо русского термина «подера» используется калька с английского «педаль»Шаблон:SfnШаблон:Sfn.

Антиподе́ра, или (первая) негативная подераШаблон:SfnШаблон:SfnШаблон:Sfn (Шаблон:Lang-en), кривой относительно точки — кривая, подера которой относительно той же точки есть исходная криваяШаблон:SfnШаблон:SfnШаблон:Sfn. Другими словами, антиподера — огибающая кривая перпендикуляров, проведённых через точки исходной кривой к прямым, соединяющим точки исходной кривой с фиксированной точкой — полюсомШаблон:Sfn.
Например, парабола есть антиподера прямой, если полюс антиподеры совпадает с фокусом параболыШаблон:SfnШаблон:Sfn, как показано на рисунке справа.
Построение антиподеры исходя из уже построенной её подеры называется построением с помощью подерыШаблон:Sfn.
Например, всегда получится коническое сечение, если осуществить построение с помощью подеры из окружности или прямойШаблон:SfnШаблон:Sfn.
Поде́ры степене́й вы́ше пе́рвой обеих разновидностей определяются как подеры подер предыдущей степени с одним и тем же полюсомШаблон:Sfn.
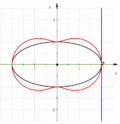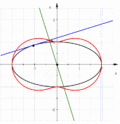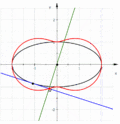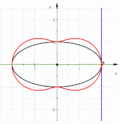
- Подеры кубики Чирнгауза и антиподеры секстики Кэли шести степеней
-
Прямая — 2-я подера кубики Чирнгауза, парабола — 5-я антиподера секстики Кэли
-
Точка — 3-я подера кубики Чирнгауза, прямая — 4-я антиподера секстики Кэли
-
Окружность — 4-я подера кубики Чирнгауза, точка — 3-я антиподера секстики Кэли
-
Кардиоида — 5-я подера кубики Чирнгауза, окружность — 2-я антиподера секстики Кэли
-
Секстика Кэли — 6-я подера кубики Чирнгауза, кардиоида — 1-я антиподера секстики Кэли
Определение подеры через инверсию и полярное преобразование

Имеет место схема преобразований кривых для подеры, инверсии и полярного преобразования кривой, показанная на рисунке справа, из которой вытекает следующее утверждениеШаблон:Sfn:
- подера кривой есть инверсия полярного преобразования кривой, окружности преобразования которых совпадают, а полюсы совпадают с полюсом подеры.
Другие связанные определения
Шаблон:Основная статья Поде́рное преобразова́ние — преобразование плоскости, отображающее точки каждой кривой в соответствующие точки её подеры. Это преобразование неточечное, то есть оно не сохраняет точки, прямые и окружностиШаблон:Sfn. Подерное преобразование есть касательное преобразование (преобразование Ли)Шаблон:Sfn.
Шаблон:Основная статья Поде́рная систе́ма координа́т — система координат, основанная на подерном преобразовании и состоящие из двух величин: расстояний от полюса до точки кривой и до соответствующей точки её подерыШаблон:SfnШаблон:Sfn.
Поде́ра пове́рхности, или подерная поверхностьШаблон:Sfn — некоторая поверхность, составленная из оснований перпендикуляров, опущенных из постоянной точки на касательные плоскости данной поверхностиШаблон:SfnШаблон:Sfn.
Подо́ида, или втори́чная ка́устика (Шаблон:Lang-en), кривой относительно данного полюса — кривая, получающаяся из подеры растяжением в два раза относительно полюсаШаблон:SfnШаблон:Sfn. Другими словами, подоида — некоторая кривая, составленная из точек, симметричных полюсу относительно касательных данной кривойШаблон:SfnШаблон:SfnШаблон:Sfn. Эволюта ортотомики есть каустикаШаблон:Sfn.
В некоторых математических текстах вместо русского термина «подоида» используется калька с английского «ортото́мика»Шаблон:Sfn.
Например, подоида конического сечения относительно его фокуса естьШаблон:Sfn:
- окружность с центром в другом фокусе эллипса или гиперболы;
- директриса параболы.
Антиподо́ида кривой относительно полюса — кривая, подоида которой относительно полюса есть исходная криваяШаблон:Sfn. Другими словами, антиподоида — огибающая кривая перпендикуляров, проведённых через середины отрезков, соединяющих точки исходной кривой с полюсомШаблон:Sfn.
Контраподе́раШаблон:SfnШаблон:Sfn, или норма́льная поде́ра, или норма́льная поде́рная кри́вая (Шаблон:Lang-en), кривой относительно полюса — подера эволюты этой кривой относительно того же полюса. Другими словами, котраподера — некоторая кривая, составленная из оснований перпендикуляров, опущенных из полюса на нормали данной кривойШаблон:SfnШаблон:SfnШаблон:Sfn. Соответственно, подера кривой относительно полюса — это контраподера эвольвенты этой кривой относительно того же полюсаШаблон:Sfn
Уравнения подеры
Параметрические уравнения подеры
Параметрические уравнения подеры на вещественной плоскости
В общем случае, для параметрически заданной кривой , имеющей производную , подера
относительно точки задаётся следующими уравнениямиШаблон:SfnШаблон:Sfn:
Эти основные уравненияШаблон:Sfn можно принять за определение подерыШаблон:Sfn.
Иногда основные уравнения записывают в более сложном видеШаблон:Sfn:
В частном случае, относительно полюса в начале координат, основные уравнения будут такимиШаблон:SfnШаблон:Sfn:
Параметрические уравнения подеры в двумерном векторном пространстве
В векторном виде основное уравнение будет прощеШаблон:Sfn:
или в более сложном видеШаблон:Sfn:
где — вектор нормали, перпендикулярный касательнойШаблон:Sfn.
Относительно полюса Шаблон:SfnШаблон:SfnШаблон:Sfn:
или в более сложном видеШаблон:SfnШаблон:SfnШаблон:Sfn:
Параметрические уравнения подеры на комплексной плоскости
В комплексных числах для параметрически заданной кривой , имеющей производную , основное уравнение подеры
относительно точки будут ещё прощеШаблон:SfnШаблон:Sfn:
В частном случае, относительно полюса , основное уравнение будет такимШаблон:SfnШаблон:Sfn:
Параметрические уравнения подеры в вещественном пространстве
Для параметрически заданной пространственной кривой , имеющей производную , подера относительно точки задаётся следующими уравнениямиШаблон:Sfn:
Прямоугольная система координат
Для кривой с неявным уравнением , имеющей частные производные и подера относительно точки задаётся следующими параметрическими уравнениямиШаблон:Sfn:
Для поверхности с неявным уравнением , имеющей частные производные , и , подера относительно точки задаётся следующими параметрическими уравнениямиШаблон:Sfn:
Подерная система координат
Самое простое уравнение подеры получается в подерной системе координат. Для кривой, имеющей подерное уравнение
- или
относительно некоторого полюса, подерное уравнение её подеры
- или
относительно того же полюсаШаблон:Sfn
Примеры подеры
Подера окружности
Шаблон:Основная статья Подера окружности с полюсом в центре есть та же самая окружность. Подера окружности с полюсом вне центра есть улитка Паскаля, в частности, если полюс подеры лежит на самой окружности, то подера — кардиоидаШаблон:Sfn.
- Подеры окружности
-
Гиперболическая улитка Паскаля — полюс подеры вне окружности
-
Кардиоида — полюс подеры на окружности
-
Эллиптическая улитка Паскаля — полюс подеры внутри окружности, но не в её центре
Найдём уравнение подеры окружности. Уравнение окружности в комплексном параметрическом виде
где — постоянный комплексный центр окружности; — постоянный вещественный радиус окружности; — вещественный параметр. Получаем:
и уравнение подеры окружности с полюсом , то есть улитки ПаскаляШаблон:Sfn:
Уравнение улитки Паскаля упростится, если прямая параллельна вещественной оси комплексной плоскости, то есть или
Рассмотрим два частных случая подерыШаблон:Sfn:
- если и совпадают, то есть подера окружности есть сама окружность с центром в начале координат — полюсе подеры:
- если лежит на окружности, то есть имеем уравнение кардиоиды с центром в каспе — полюсе подеры:
- если при этом прямая параллельна вещественной оси комплексной плоскости, то есть или то уравнение кардиоиды
- а если при этом окружность имеет радиус и слева от , то самое простое уравнение кардиоиды
Подера параболы
Любая парабола имеет подеру — циркулярную кривую 3-го порядка на комплексной проективной плоскостиШаблон:Sfn.
Не умаляя общности, уравнение произвольной параболы можно записать в следующем видеШаблон:Sfn:
- или
где — расстояние от фокуса параболы до её вершины и от вершины до директрисы.
Тогда подера произвольной параболы относительно произвольного полюса есть дефективная гипербола с двойной точкой , асимптотой и следующим уравнениемШаблон:Sfn:
Подера эллипса
Подера эллипса
- относительно его фокуса — окружность,
- относительно центра эллипса — лемниската Бута.
- Подеры эллипса
-
Окружность — полюс подеры в фокусе эллипса
-
Лемниската Бута — полюс подеры в центре эллипса. Здесь a=2 b=1, уравнение 4x2+y2=(x2+y2)2