Дифференцирование тригонометрических функций

Функция синуса и косинуса в единичном круге

Функция	Производная
$\sin (x)$	$\cos (x)$
$\cos (x)$	$-\sin (x)$
$\tan (x)$	${\sec }^2(x)$
$\cot (x)$	$-{\csc }^2(x)$
$\sec (x)$	$\sec (x)\tan (x)$
$\csc (x)$	$-\csc (x)\cot (x)$
$\arcsin (x)$	$\frac{1}{\sqrt{1-x^2}}$
$\arccos (x)$	$-\frac{1}{\sqrt{1-x^2}}$
$\arctan (x)$	$\frac{1}{x^2+1}$
$\mathrm{arccot}(x)$	$-\frac{1}{x^2+1}$
$\mathrm{arcsec}(x)$	$\frac{1}{|x|\sqrt{x^2-1}}$
$\mathrm{arccsc}(x)$	$-\frac{1}{|x|\sqrt{x^2-1}}$

Дифференцирование тригонометрических функций — математический процесс нахождения производной тригонометрической функции или скорости её изменения по отношению к переменной. Например, производная функции синуса записывается как sin′(a) = cos(a), что означает, что скорость изменения sin(x) под определённым углом x = a задаётся косинусом этого угла.

Все производные круговых тригонометрических функций могут быть найдены из производных sin(x) и cos(x) с помощью Шаблон:Нп5, применяемого к таким функциям, как tan(x) = sin(x)/cos(x). Зная эти производные, можно производные от обратных тригонометрических функций найти с помощью неявного дифференцирования.

Все указанные функции непрерывны и дифференцируемы в своей области определения.

Доказательства производных тригонометрических функций

Предел sin(θ)/θ при стремлении θ к 0

Круг с центром O и радиусом r
(r = OK = OA)

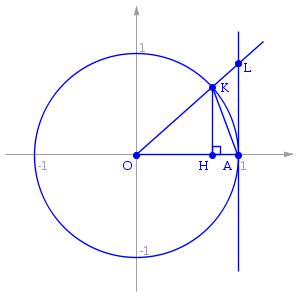
На диаграмме справа показан круг с центром O и радиусом r = 1. Пусть два радиуса OA и OK образуют дугу в θ радиан. Поскольку мы рассматриваем предел, когда θ стремится к нулю, мы можем предположить, что θ — это небольшое положительное число, скажем, 0 < θ < ½ π в первом квадранте.

На схеме пусть R₁ будет треугольником OAK, R₂ — круговым сектором KOA и R₃ — треугольником OAL. Тогда площадь треугольника OAK:

$\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}(R_1)=\frac{1}{2}|OA||OK|\sin \theta =\frac{1}{2}\sin \theta .$

Площадь кругового сектора OAK — это $\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}(R_2)=\frac{1}{2}\theta$, а площадь треугольника OAL определяется как

$\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}(R_3)=\frac{1}{2}|OA||AL|=\frac{1}{2}|AL|=\frac{1}{2}\tan \theta .$

Поскольку каждый объект содержится в следующем, мы имеем:

$\text{Area}(R_1)<\text{Area}(R_2)<\text{Area}(R_3)⟺\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta .$

Более того, поскольку Шаблон:Nowrap в первом квадранте, мы можем разделить на ½ Шаблон:Nowrap, получив:

$1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }⟹1>\frac{\sin \theta }{\theta }>\cos \theta .$

На последнем этапе мы взяли обратно три положительных члена, изменив неравенство.

Мы пришли к выводу, что для 0 < θ < ½ π выражение Шаблон:Ы будет всегда меньше 1 и всегда больше cos(θ). Таким образом, чем ближе θ к 0, тем сильнее Шаблон:Ы становится "сжатым" между потолком на высоте 1 и полом на высоте Шаблон:Ы, который стремится к 1; следовательно, sin(θ)/θ стремится к 1, когда θ стремится к 0 с положительной стороны:

$\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1.$

Для случая, когда θ — это небольшое отрицательное число -½ π <θ <0, мы используем тот факт, что синус — это нечётная функция:

$\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{\sin (-\theta )}{-\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{-\sin \theta }{-\theta }=\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1.$

Предел (cos(θ)-1)/θ при стремлении θ к 0

Последний раздел позволяет нам относительно легко рассчитать этот новый предел. Это делается простым трюком. В этом расчёте знак θ неважен.

$\underset{\theta \to 0}{\lim }\frac{\cos \theta -1}{\theta }=\underset{\theta \to 0}{\lim }\left(\frac{\cos \theta -1}{\theta }\right)\left(\frac{\cos \theta +1}{\cos \theta +1}\right)=\underset{\theta \to 0}{\lim }\frac{{\cos }^2\theta -1}{\theta (\cos \theta +1)}.$

С использованием Шаблон:Ы факт, что предел произведения является произведением пределов, а предельный результат из предыдущего раздела, мы находим, что:

$\underset{\theta \to 0}{\lim }\frac{\cos \theta -1}{\theta }=\underset{\theta \to 0}{\lim }\frac{-{\sin }^2\theta }{\theta (\cos \theta +1)}=(-\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta })\left(\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\cos \theta +1}\right)=(-1)\left(\frac{0}{2}\right)=0.$

Предел tan(θ)/θ при стремлении θ к 0

Используя предел для функции синуса и то, что функция тангенс нечётна и предел произведения является произведением пределов, мы находим:

$\underset{\theta \to 0}{\lim }\frac{\tan \theta }{\theta }=\left(\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta }\right)\left(\underset{\theta \to 0}{\lim }\frac{1}{\cos \theta }\right)=(1)(1)=1.$

Производная функции синуса

Из определения производной

Мы рассчитываем производную функции синуса из определения предела:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =\underset{\delta \to 0}{\lim }\frac{\sin (\theta +\delta )-\sin \theta }{\delta }.$

Используя формулы сложения углов Шаблон:Ы, мы имеем:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =\underset{\delta \to 0}{\lim }\frac{\sin \theta \cos \delta +\sin \delta \cos \theta -\sin \theta }{\delta }=\underset{\delta \to 0}{\lim }(\frac{\sin \delta }{\delta }\cos \theta +\frac{\cos \delta -1}{\delta }\sin \theta ).$

Использование пределов для функций синуса и косинуса:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =(1)\cos \theta +(0)\sin \theta =\cos \theta .$

Из производной гиперболических функций

Если использовать гиперболические функции, то формально можно получить, что:

$\frac{d}{dx}\sin (x)=-\frac{d}{dx}i\mathrm{sh}(ix)=\mathrm{ch}(ix)=\cos (x)$,

т.к.

$\sin (x)=\frac{\exp (ix)-\exp (-ix)}{2i}=\frac{\mathrm{sh}(ix)}{i}=-i\mathrm{sh}(ix);$

$\cos (x)=\frac{\exp (ix)+\exp (-ix)}{2}=\mathrm{ch}(ix)$

Производная функции косинуса

Из определения производной

Мы снова вычисляем производную функции косинуса из определения предела:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =\underset{\delta \to 0}{\lim }\frac{\cos (\theta +\delta )-\cos \theta }{\delta }.$

Используя формулу сложения углов Шаблон:Ы, мы имеем:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =\underset{\delta \to 0}{\lim }\frac{\cos \theta \cos \delta -\sin \theta \sin \delta -\cos \theta }{\delta }=\underset{\delta \to 0}{\lim }(\frac{\cos \delta -1}{\delta }\cos \theta -\frac{\sin \delta }{\delta }\sin \theta ).$

Использование пределов для функций синуса и косинуса:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =(0)\cos \theta -(1)\sin \theta =-\sin \theta .$

Из производной гиперболических функций

Если использовать гиперболические функции, то формально можно получить, что:

$\frac{d}{dx}\cos (x)=\frac{d}{dx}i\mathrm{ch}(ix)=i\mathrm{sh}(ix)=-\sin (x)$

Из цепного правила

Чтобы вычислить производную функции косинуса из цепного правила, сначала обратите внимание на три следующих факта:

$\cos \theta =\sin (\frac{\pi }{2}-\theta )$

$\sin \theta =\cos (\frac{\pi }{2}-\theta )$

$\frac{\mathrm{d}}{\mathrm{d}\theta }\sin \theta =\cos \theta$

Первое и второе — это тригонометрические тождества, а третье доказано выше. Используя эти три факта, мы можем написать следующее:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =\frac{\mathrm{d}}{\mathrm{d}\theta }\sin (\frac{\pi }{2}-\theta )$

Мы можем дифференцировать это, используя цепное правило. Положив $f(x)=\sin x,g(\theta )=\frac{\pi }{2}-\theta$, мы имеем:

$\frac{\mathrm{d}}{\mathrm{d}\theta }f\left(g\left(\theta \right)\right)=f^{\prime }\left(g\left(\theta \right)\right)\cdot g^{\prime }\left(\theta \right)=\cos (\frac{\pi }{2}-\theta )\cdot (0-1)=-\sin \theta$.

Таким образом, мы доказали, что

$\frac{\mathrm{d}}{\mathrm{d}\theta }\cos \theta =-\sin \theta$.

Производная функции тангенса

Из определения производной

Чтобы вычислить производную функции тангенса tan θ, мы используем первые принципы. По определению:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =\underset{\delta \to 0}{\lim }\left(\frac{\tan (\theta +\delta )-\tan \theta }{\delta }\right).$

Используя известную формулу угла Шаблон:Ы, мы имеем:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =\underset{\delta \to 0}{\lim }\left[\frac{\frac{\tan \theta +\tan \delta }{1-\tan \theta \tan \delta }-\tan \theta }{\delta }\right]=\underset{\delta \to 0}{\lim }\left[\frac{\tan \theta +\tan \delta -\tan \theta +{\tan }^2\theta \tan \delta }{\delta (1-\tan \theta \tan \delta )}\right].$

Используя тот факт, что предел произведения является произведением пределов:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =\underset{\delta \to 0}{\lim }\frac{\tan \delta }{\delta }\times \underset{\delta \to 0}{\lim }\left(\frac{1+{\tan }^2\theta }{1-\tan \theta \tan \delta }\right).$

Используя предел для функции тангенса и тот факт, что tan δ стремится к 0, поскольку δ стремится к 0:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =1\times \frac{1+{\tan }^2\theta }{1-0}=1+{\tan }^2\theta .$

Сразу видим, что:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =1+\frac{{\sin }^2\theta }{{\cos }^2\theta }=\frac{{\cos }^2\theta +{\sin }^2\theta }{{\cos }^2\theta }=\frac{1}{{\cos }^2\theta }={\sec }^2\theta .$

Из производной гиперболических функций

$\frac{d}{dx}\tan (x)=-i\frac{d}{dx}\mathrm{th}(ix)=-i\frac{i}{{\mathrm{ch}}^2(ix)}=\frac{1}{{\mathrm{ch}}^2(ix)}=\frac{1}{{\cos }^2(x)}$

Из правила частного

Также можно вычислить производную функции тангенса, используя правило частного:

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta =\frac{\mathrm{d}}{\mathrm{d}\theta }\frac{\sin \theta }{\cos \theta }=\frac{{(\sin \theta )}^{\prime }\cdot \cos \theta -\sin \theta \cdot {(\cos \theta )}^{\prime }}{{\cos }^2\theta }=\frac{{\cos }^2\theta +{\sin }^2\theta }{{\cos }^2\theta }$

Числитель можно упростить до 1 с помощью пифагорового тождества, что даёт нам:

$\frac{1}{{\cos }^2\theta }={\sec }^2\theta$

Следовательно,

$\frac{\mathrm{d}}{\mathrm{d}\theta }\tan \theta ={\sec }^2\theta$

Доказательства производных обратных тригонометрических функций

Следующие производные можно найти, установив переменную y равной обратной тригонометрической функции, от которой мы хотим взять производную. Используя неявное дифференцирование и затем решая для dy/dx, производная обратной функции будет найдена в терминах y. Чтобы преобразовать dy/dx обратно в термины x, мы можем нарисовать эталонный треугольник на единичной окружности, положив θ равным y. Используя теорему Пифагора и определение обычных тригонометрических функций, мы наконец можем выразить dy/dx через x.

Дифференцирование функции арксинуса

Пусть

$y=\arcsin x,$

где

$-\frac{\pi }{2}\le y\le \frac{\pi }{2}.$

Тогда

$\sin y=x.$

Взяв производную по $x$ с обеих сторон и решив для $dy/dx$, имеем:

$\frac{d}{dx}\sin y=\frac{d}{dx}x,$

$\cos y\cdot \frac{dy}{dx}=1.$

Подставляя сверху $\cos y=\sqrt{1-{\sin }^{2}y}$, имеем:

$\sqrt{1-{\sin }^{2}y}\cdot \frac{dy}{dx}=1$

Подставляя сверху $x=\sin y$, имеем:

$\sqrt{1-x^2}\cdot \frac{dy}{dx}=1$

$\frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}}$

Из производной обратной гиперболической функции

$\frac{d}{dx}\arcsin (x)=-i\frac{d}{dx}\mathrm{arsh}(ix)=-i\frac{i}{\sqrt{1+i^2{x}^2}}=\frac{1}{\sqrt{1-x^2}}$

Дифференцирование функции арккосинуса

Пусть

$y=\arccos x$

где

$0\le y\le \pi$

Тогда

$\cos y=x$

Взяв производную по $x$ с обеих сторон и решив для $dy/dx$, имеем:

$\frac{d}{dx}\cos y=\frac{d}{dx}x$

$-\sin y\cdot \frac{dy}{dx}=1$

Подставляя сверху $\sin y=\sqrt{1-{\cos }^{2}y}$, получаем:

$-\sqrt{1-{\cos }^{2}y}\cdot \frac{dy}{dx}=1$

Подставляя сверху $x=\cos y$, получаем:

$-\sqrt{1-x^2}\cdot \frac{dy}{dx}=1$

$\frac{dy}{dx}=-\frac{1}{\sqrt{1-x^2}}$

В качестве альтернативы, как только производная от $\arcsin x$ установлена, производная от $\arccos x$ сразу следует путём дифференцирования тождества $\arcsin x+\arccos x=\pi /2$ так, что $(\arccos x{)}^{\prime }=-(\arcsin x{)}^{\prime }$.

Из производной обратной гиперболической функции

$\frac{d}{dx}\arccos (x)=-i\frac{d}{dx}\mathrm{arch}(ix)=-i\frac{i}{\sqrt{i^2{x}^2-1}}=-\frac{1}{\sqrt{1-x^2}}$

Дифференцирование функции арктангенса

Пусть

$y=\arctan x$

где

$-\frac{\pi }{2}<y<\frac{\pi }{2}$

Тогда

$\tan y=x$

Взяв производную по $x$ с обеих сторон и решив для $dy/dx$, имеем:

$\frac{d}{dx}\tan y=\frac{d}{dx}x$

Левая сторона:

$\frac{d}{dx}\tan y={\sec }^{2}y\cdot \frac{dy}{dx}=(1+{\tan }^{2}y)\frac{dy}{dx}$, используя пифагорово тождество

Правая сторона:

$\frac{d}{dx}x=1$

Следовательно,

$(1+{\tan }^{2}y)\frac{dy}{dx}=1$

Подставляя сверху $x=\tan y$, получаем:

$(1+x^2)\frac{dy}{dx}=1$

$\frac{dy}{dx}=\frac{1}{1+x^2}$

Из производной обратной гиперболической функции

$\frac{d}{dx}\arctan (x)=-i\frac{d}{dx}\mathrm{arth}(ix)=-i\frac{i}{1-i^2{x}^2}=\frac{1}{1+x^2}$

Дифференцирование функции арккотангенса

Пусть

$y=\mathrm{arccot}x$

где $0<y<\pi$ Тогда

$\cot y=x$

Взяв производную по $x$ с обеих сторон и решив для $dy/dx$, имеем:

$\frac{d}{dx}\cot y=\frac{d}{dx}x$

Левая сторона:

$\frac{d}{dx}\cot y=-{\csc }^{2}y\cdot \frac{dy}{dx}=-(1+{\cot }^{2}y)\frac{dy}{dx}$, используя пифагорово тождество

Правая сторона:

$\frac{d}{dx}x=1$

Следовательно,

$-(1+{\cot }^{2}y)\frac{dy}{dx}=1$

Подставляя $x=\cot y$, получаем:

$-(1+x^2)\frac{dy}{dx}=1$

$\frac{dy}{dx}=-\frac{1}{1+x^2}$

Из производной обратной гиперболической функции

$\frac{d}{dx}\mathrm{arccot}(x)=i\frac{d}{dx}\mathrm{arcth}(ix)=i\frac{i}{1-i^2{x}^2}=-\frac{1}{1+x^2}$

Дифференцирование функции арксеканса

Использование неявного дифференцирования

Пусть

$y=\mathrm{arcsec}x|x|\ge 1$

Тогда

$x=\sec yy\in [0,\frac{\pi }{2})\cup (\frac{\pi }{2},\pi ]$

$\frac{dx}{dy}=\sec y\tan y=|x|\sqrt{x^2-1}$

(Абсолютное значение в выражении необходимо, поскольку произведение секанса и тангенса в интервале y всегда неотрицательно, а радикал $\sqrt{x^2-1}$ всегда неотрицателен по определению главного квадратного корня, поэтому оставшийся множитель также должен быть неотрицательным, что достигается за счёт использования абсолютного значения x.)

$\frac{dy}{dx}=\frac{1}{|x|\sqrt{x^2-1}}$

Использование цепного правила

В качестве альтернативы, производная арксеканса может быть получена из производной арккосинуса с использованием цепного правила.

Пусть

$y=\mathrm{arcsec}x=\arccos \left(\frac{1}{x}\right)$

где

$|x|\ge 1$ and $y\in [0,\frac{\pi }{2})\cup (\frac{\pi }{2},\pi ]$

Тогда, применяя цепное правило к $\arccos \left(\frac{1}{x}\right)$, имеем:

$\frac{dy}{dx}=-\frac{1}{\sqrt{1-(\frac{1}{x}{)}^2}}\cdot (-\frac{1}{x^2})=\frac{1}{x^2\sqrt{1-\frac{1}{x^2}}}=\frac{1}{x^2\frac{\sqrt{x^2-1}}{\sqrt{x^2}}}=\frac{1}{\sqrt{x^2}\sqrt{x^2-1}}=\frac{1}{|x|\sqrt{x^2-1}}$

Дифференцирование функции арккосеканса

Использование неявного дифференцирования

Пусть

$y=\mathrm{arccsc}x|x|\ge 1$

Тогда

$x=\csc yy\in [-\frac{\pi }{2},0)\cup (0,\frac{\pi }{2}]$

$\frac{dx}{dy}=-\csc y\cot y=-|x|\sqrt{x^2-1}$

(Абсолютное значение в выражении необходимо, поскольку произведение косеканса и котангенса в интервале y всегда неотрицательно, а радикал $\sqrt{x^2-1}$ всегда неотрицателен по определению главного квадратного корня, поэтому оставшийся множитель также должен быть неотрицательным, что достигается за счёт использования абсолютного значения x.)

$\frac{dy}{dx}=\frac{-1}{|x|\sqrt{x^2-1}}$

Использование цепного правила

В качестве альтернативы, производная арккосеканса может быть получена из производной арксинуса с использованием цепного правила.

Пусть

$y=\mathrm{arccsc}x=\arcsin \left(\frac{1}{x}\right)$

где

$|x|\ge 1$ and $y\in [-\frac{\pi }{2},0)\cup (0,\frac{\pi }{2}]$

Тогда, применяя цепное правило к $\arcsin \left(\frac{1}{x}\right)$, имеем:

$\frac{dy}{dx}=\frac{1}{\sqrt{1-(\frac{1}{x}{)}^2}}\cdot (-\frac{1}{x^2})=-\frac{1}{x^2\sqrt{1-\frac{1}{x^2}}}=-\frac{1}{x^2\frac{\sqrt{x^2-1}}{\sqrt{x^2}}}=-\frac{1}{\sqrt{x^2}\sqrt{x^2-1}}=-\frac{1}{|x|\sqrt{x^2-1}}$

См. также

• Тригонометрия
• Математический анализ
• Производная функции
• Таблица производных

Литература

• Шаблон:Нп5, Под редакцией Абрамовица и Стегуна, Национальное бюро стандартов, Серия по прикладной математике, 55 (1964)
• Шаблон:Книга