Усечение (геометрия)

Шаблон:Значения

Усечённый квадрат является правильным восьмиугольником: t{4} = {8} Шаблон:CDD = Шаблон:CDD	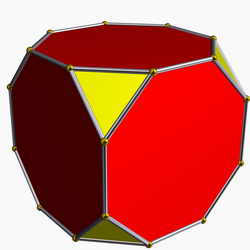Усечённый куб t{4,3} или Шаблон:CDD	Шаблон:Не переведено 5 t{4,3,4} или Шаблон:CDD

Усечение — операция в пространстве любой размерности, которая отсекает вершины многогранника и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.

Однородное отсечение

В общем случае любой многогранник может быть усечён с некоторой степенью свободы выбора глубины усечения, что показано в статье Нотация Конвея для многогранников.

Обычно применяемый вид усечения — однородное усечение, при котором операция усечения применяется к правильному многограннику и результатом которого получается однородный многогранник с равными длинами рёбер. В этом случае нет свободы выбора и в результате получаем вполне определённые геометрические тела, похожие на правильные многогранники.

В общем случае все однородные многогранники с одним обведённым узлом (в диаграмме Коксетера — Дынкина) имеют однородное усечение. Например, икосододекаэдр, представленный символами Шлефли r{5,3} или ${\begin{matrix} 5 \\ 3 \end{matrix}}$ и имеющий диаграммы Коксетера — Дынкина Шаблон:CDD или Шаблон:CDD, имеет однородное усечение — ромбоусечённый икосододекаэдр с нотациями tr{5,3} или $t {\begin{matrix} 5 \\ 3 \end{matrix}}$ , Шаблон:CDD. В диаграмме Коксетера — Дынкина эффект усечения проявляется в том, что у всех узлов, смежных с обведённым, появляются кружки.

Усечение многоугольников

Усечённый n-сторонний многоугольник будет иметь 2n сторон. Однородно усечённый правильный многоугольник становится другим правильным многоугольником: t{n} = {2n}. Полное усечение, r{3}, является другим правильным многоугольником, Шаблон:Не переведено 5 исходному.

Правильные многоугольники можно также представить диаграммой Коксетера — Дынкина, Шаблон:CDD, и его однородное усечение будет иметь диаграмму Шаблон:CDD, а его полное усечение — диаграмму Шаблон:CDD. Граф Шаблон:CDD представляет группу Коксетера I₂(n), в которой каждый узел является зеркалом, а каждое ребро представляет угол π/n между зеркалами, кружки же вокруг одного или двух зеркал показывают, какие из них активны.

Параметрическое усечение треугольника
{3} Шаблон:CDD		t{3} = {6} Шаблон:CDD		r{3} = {3} Шаблон:CDD

Звёздчатые многоугольники могут быть тоже усечены. Усечённая пентаграмма {5/2} будет выглядеть как пятиугольник, но, в действительности, является дважды накрытым (вырожденным) десятиугольником ({10/2}) с двумя множествами наложенных друг на друга вершин и сторон. Усечённая большая гептаграмма (семиугольная звезда) {7/3} даёт четырнадцатиугольную звезду {14/3}.

Однородное усечение правильных многогранников и мозаик

Когда речь идёт об усечении правильных многогранников или Шаблон:Не переведено 5, обычно использыется «однородное усечение», что предполагает усечение до состояния, когда исходные грани становятся правильными многоугольниками с удвоенным числом сторон.

Файл:Cube truncation sequence(ru).svg

Последовательность на рисунке показывает пример усечения куба, где показаны четыре шага из непрерывного процесса усечения от полного куба до полного усечения куба. Конечное тело — кубооктаэдр.

Среднее изображение является однородным усечённым кубом. Он представлен символом Шлефли t{p,q,…}.

Шаблон:Не переведено 5 — это более сильное усечение, удаляющее все исходные рёбра, но оставляющие внутренние части исходных граней. Например, усечённый октаэдр является глубоко усечённым кубом: 2t{4,3}.

Полное глубокое усечение называется биректификацией и оно сводит исходные грани к точкам. Многогранник при этом превращается в двойственный многогранник. Например, октаэдр является полным глубоким усечением куба: {3,4} = 2r{4,3}.

Ещё один тип усечения — всестороннее усечение, при котором отсекаются рёбра и вершины, что даёт прямоугольники вместо рёбер.

Многогранники в более высоких размерностях имеют другие уровни усечений — Шаблон:Не переведено 5, при которой отсекаются грани, рёбра и вершины. В размерностях выше 5 существует Шаблон:Не переведено 5, при которой отсекаются грани, рёбра и вершины, а также трёхмерные грани.

Усечение рёбер

Усечение рёбер — это снятие фаски с многогранника, как в случае всестороннего усечения, но вершины при этом остаются, а рёбра заменяются шестиугольниками. В 4-мерном многограннике рёбра заменяются на Шаблон:Не переведено 5.

Альтернации или частичные усечения

Альтернация или частичное усечение удаляет только некоторые из исходных вершин.

При частичном усечении или Шаблон:Не переведено 5 половина вершин и рёбер полностью удаляется. Операция применима к многогранникам, грани которого имеют чётное число сторон. Грани сокращают число сторон вдвое, а квадратные грани переходят рёбра. Например, тетраэдр является альтернацией куба, h{4,3}.

Шаблон:Не переведено 5 — более общий термин, использующийся для многогранников Джонсона, предполагает удаление одной или более вершин, рёбер или граней не трогая оставшиеся вершины. Например, Шаблон:Не переведено 5 получается из правильного икосаэдра путём удаления трёх вершин.

Другие частичные усечения основываются на симметрии. Например, Шаблон:Не переведено 5.

Обобщённые усечения

Файл:Types of truncation on edge(ru).svg

Типы усечения показаны для ребра, принадлежащего многоугольнику или многограннику с голубыми и красными вершинами. Ребро меняет ориентацию после полного усечения.

Процесс линейного усечения может быть обобщён путём разрешения параметра усечения быть отрицательным или разрешения проходить через середину ребра, что даёт самопересекающиеся звёздчатые многогранники. Такие многогранники могут быть связаны с некоторыми Шаблон:Не переведено 5 и однородными звёздчатыми многогранниками.

Мелкое усечение — рёбра уменьшаются в размерах, грани удваивают число сторон, на месте бывших вершин образуются новые грани.
Однородное усечение — специальный случай, при котором все полученные рёбра имеют одинаковую длину. В усечённом кубе, t{4,3}, квадратные грани превращаются в восьмиугольники, а вместо вершин образуются треугольники.
Антиусечение обратно мелкому усечению. В результате получается многогранник, который похож на исходный, но имеет части, висящие на углах, вместо отрезания углов.
Полное усечение — предельное мелкое усечение, где рёбра сводятся к точкам. Примером служит Кубооктаэдр, r{4,3}.
Гиперусечение является видом усечения, которое идёт далее полного усечения, обращая исходные рёбра, что приводит к самопересечениям.
Квазиусечение является видом усечения, идущего далее гиперусечения, где обращённые рёбра становятся длиннее исходных. Это усечение можно получить из исходного многогранника путём отступления граней от рёбер, то есть движению в обратную сторону от вершины. Например, квазиусечение квадрата даёт правильную октаграмму (t{4,3}={8/3}), а квазиусечение куба даёт однородный Шаблон:Не переведено 5, t{4/3,3}.

Усечения квадрата
Типы усечения квадрата, {4}. Исходные рёбра показаны красным цветом, а новые рёбра, полученные в результате усечения — голубым. Однородное усечение является правильным восьмиугольником, t{4}={8}. Полное усечение квадрата становится опять квадратом с диагональной ориентацией сторон. Вершины пронумерованы против часовой стрелки цифрами от 1 до 4, полученные в результате усечения пары отмечены буквами a и b.

Усечения куба
⇨	Куб {4,3}	⇨	Усечение t{4,3}	⇨	Полное усечение r{4,3}	⇩
Антиусечение						Гиперусечение
⇧	Полное квазиусечение	⇦	Квазиусечение Шаблон:Не переведено 5	⇦	Полное гиперусечение	⇦