Гармонический ряд

Гармони́ческий ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{k}+\cdots$.

Ряд назван гармоническим, так как складывается из «гармоник»: $k$-я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной $\frac{1}{k}$ от длины исходной струны. Кроме того, каждый член ряда, начиная со второго, представляет собой среднее гармоническое двух соседних членов.

Суммы первых n членов ряда (частичные суммы)

Отдельные члены ряда стремятся к нулю, но его сумма бесконечна (ряд расходится). Частичная сумма Шаблон:Math первых членов гармонического ряда называется Шаблон:Math-м гармоническим числом:

$H_n=\sum _{k=1}^n\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{n}$

Разность между $n$-м гармоническим числом и натуральным логарифмом $n$ сходится к постоянной Эйлера — Маскерони $\gamma =0,5772...$.

Разность между различными гармоническими числами никогда не равна целому числу и никакое гармоническое число, кроме $H_1=1$, не является целым: $\mathrm{\forall }n>1\sum _{k=1}^n\frac{1}{k}\notin \mathbb{N}$.

Некоторые значения частичных сумм

$n$	Гармонический ряд		Приближение ${\displaystyle }$
	$H_n$ (дробь)	$H_n$ (десятичная запись)	$\ln n$	$\ln n+\gamma$
1	$1$	$1$	$0$	$0,57721...$
2	$\frac{3}{2}$	$1,5$	$\approx 0,69315$	$\approx 1,27036$
3	$\frac{11}{6}$	$\approx 1,83333$	$\approx 1,09861$	$\approx 1,67583$
4	$\frac{25}{12}$	$\approx 2,08333$	$\approx 1,38629$	$\approx 1,96351$
5	$\frac{137}{60}$	$\approx 2,28333$	$\approx 1,60944$	$\approx 2,18665$
6	$\frac{49}{20}$	$2,45$	$\approx 1,79176$	$\approx 2,36898$
7	$\frac{363}{140}$	$\approx 2,59285$	$\approx 1,94591$	$\approx 2,52313$
8	$\frac{761}{280}$	$\approx 2,71786$	$\approx 2,07944$	$\approx 2,65666$
9	$\frac{7129}{2520}$	$\approx 2,82897$	$\approx 2,19722$	$\approx 2,77444$
10	$\frac{7381}{2520}$	$\approx 2,92897$	$\approx 2,30258$	$\approx 2,8798$
100		$\approx 5,18737$	$\approx 4,60517$	$\approx 5,18238$
10$3^{}$		$\approx 7.48547$	$\approx 6,90776$	$\approx 7,48497$
10$6^{}$		$\approx 14,39273$	$\approx 13,81551$	$\approx 14,39273$

Формула Эйлера

В 1740 году Эйлером было получено асимптотическое выражение для суммы первых $n$ членов ряда:

$H_n=\ln n+\gamma +{\epsilon }_n$,

где $\gamma =0,5772...$ — постоянная Эйлера — Маскерони, а $\ln$ — натуральный логарифм.

При $n\to \mathrm{\infty }$ значение ${\epsilon }_n\to 0,$ следовательно, для больших $n$

$H_n\approx \ln n+\gamma$ — формула Эйлера для суммы первых $n$ членов гармонического ряда.

Пример использования формулы Эйлера

$n$	$H_n=\sum _{k=1}^n\frac{1}{k}$	$\ln n+\gamma$	${\epsilon }_n$, (%)
10	2,93	2,88	1,7
25	3,82	3,80	0,5

Более точная асимптотическая формула для частичной суммы гармонического ряда:

$H_n\asymp \ln n+\gamma +\frac{1}{2n}-\frac{1}{12n^2}+\frac{1}{120n^4}-\frac{1}{252n^6}\dots =\ln n+\gamma +\frac{1}{2n}-\sum _{k=1}^{\mathrm{\infty }}\frac{B_{2k}}{2k{n}^{2k}},$ где $B_{2k}$ — числа Бернулли.

Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного членаШаблон:Нет АИ.

Расходимость ряда

Гармонический ряд расходится: $s_n\to \mathrm{\infty }$ при $n\to \mathrm{\infty },$ однако очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 1.5*10⁴³ элементов ряда).

Расходимость гармонического ряда можно продемонстрировать, сравнив его со следующим телескопическим рядом, который получается из логарифмирования ${(1+\frac{1}{n})}^n<e$:

$v_n=\ln (n+1)-\ln n=\ln (1+\frac{1}{n})<\frac{1}{n}.$

Частичная сумма этого ряда, очевидно, равна $\sum _{i=1}^n{v}_i=\ln (n+1).$ Последовательность таких частичных сумм расходится; следовательно, по определению телескопический ряд расходится, но тогда из признака сравнения рядов следует, что гармонический ряд тоже расходится.

Доказательство через предел последовательности частичных сумм

Рассмотрим последовательность $H_n=\sum _{k=1}^n\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots +\frac{1}{n}.$ Покажем, что эта последовательность не является фундаментальной, то есть, что $\mathrm{\exists }\epsilon >0:\mathrm{\forall }k\in \mathbb{N}\mathrm{\exists }n>k,\mathrm{\exists }p\in \mathbb{N}:|H_{n+p}-H_n|\ge \epsilon .$ Оценим разность $|H_{n+p}-H_n|=\frac{1}{n+1}+\cdots +\frac{1}{n+p}\ge \frac{1}{n+p}+\cdots +\frac{1}{n+p}=\frac{p}{n+p}.$ Пусть $p\doteq n.$ Тогда $\mathrm{\forall }n\in \mathbb{N}:|H_{2n}-H_n|\ge \frac{1}{2}.$ Следовательно, данная последовательность не является фундаментальной и по критерию Коши расходится. Тогда по определению ряд также расходится.

Доказательство Орема

Доказательство расходимости можно построить, если сравнить гармонический ряд с другим расходящимся рядом, в котором знаменатели дополнены до степени двойки. Этот ряд группируется, и получается третий ряд, который расходится:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}& =1+\left[\frac{1}{2}\right]+[\frac{1}{3}+\frac{1}{4}]+[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}]+[\frac{1}{9}+\cdots ]+\cdots \\ & >1+\left[\frac{1}{2}\right]+[\frac{1}{4}+\frac{1}{4}]+[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}]+[\frac{1}{16}+\cdots ]+\cdots \\ & =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots .\end{array}$

(Группировка сходящихся рядов всегда дает сходящийся ряд, а значит если после группировки получился ряд расходящийся, то и исходный тоже расходится.)

Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).

Связанные ряды

Обобщённый гармонический ряд

Обобщённым гармоническим рядом (частный случай ряда Дирихле) называют ряд

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^{\alpha }}=1+\frac{1}{2^{\alpha }}+\frac{1}{3^{\alpha }}+\frac{1}{4^{\alpha }}+\cdots +\frac{1}{k^{\alpha }}+\cdots$.

Этот ряд расходится при $\alpha ⩽1$ и сходится при $\alpha >1$.

Сумма обобщённого гармонического ряда порядка $\alpha$ равна значению дзета-функции Римана:

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k^{\alpha }}=\zeta (\alpha )$

Для целых чётных показателей это значение явно выражается через число пи — например, сумма ряда обратных квадратов $\zeta (2)=\frac{{\pi }^2}{6}$. Но уже для Шаблон:Math=3 его значение (константа Апери) аналитически неизвестно.

Другой иллюстрацией расходимости гармонического ряда может служить соотношение $\zeta (1+\frac{1}{n})\sim n.$

Знакопеременный ряд

Первые 14 частичных сумм знакочередующегося гармонического ряда (чёрные отрезки), показывающие сходимость к натуральному логарифму от 2 (красная линия)

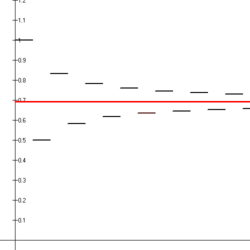
В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots$

сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью. Его сумма равна натуральному логарифму 2:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots =\ln 2.$

Эта формула — частный случай ряда Меркатора, то есть ряда Тейлора для натурального логарифма.

Похожий ряд может быть получен из ряда Тейлора для арктангенса:

$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\frac{\pi }{4}.$

Это соотношение известно как ряд Лейбница.

Случайный гармонический ряд

В 2003 году изучены свойства случайного ряда

$\sum _{n=1}^{\mathrm{\infty }}\frac{s_n}{n},$

где $s_n$ — независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что этот ряд сходится с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2, имеет значение:

Шаблон:Num…,

отличаясь от ⅛ на менее чем 10⁻⁴².

«Истончённый» гармонический ряд

См. Шаблон:Нп5

Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшийся ряд сходится, и его сумма меньше 80. Позже была найдена более точная оценка, ряд Кемпнера сходится к $22,92067661926415034816$ (Шаблон:OEIS). Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться. Из этого можно сделать ошибочное заключение о сходимости исходного гармонического ряда, что не верно, поскольку с ростом разрядов в числе $n$ всё меньше слагаемых берётся для суммы «истончённого» ряда. То есть, в конечном счёте отбрасывается подавляющее большинство членов, образующих сумму гармонического ряда, чтобы не превзойти ограничивающую сверху геометрическую прогрессию.