Температурные функции Грина

Температурные функции Грина являются некоторой модификацией функций Грина для квантовомеханических систем с температурой отличной от нуля. Они удобны для вычисления термодинамических свойств системы, а также содержат информацию о спектре квазичастиц и о слабонеравновесных кинетических явлениях.

В системах со взаимодействием может быть построена соответствующая диаграммная техника для температурных функций Грина. Эта техника широко используется для изучения фазовых переходов (сверхпроводимость, сверхтекучесть, точка Кюри) в различных системах. Исследование подобных систем является нетривиальной задачей. Для описания самого механизма перехода и состояния ниже точки перехода модель невзаимодействующих частиц непригодна. Здесь решающую роль играет межчастичное взаимодействие. Учёт подобного взаимодействия значительно усложняет используемый математический аппарат. Аппарат температурных функций Грина можно развивать в двух эквивалентных формулировках: с помощью квантовомеханических операторов либо в методе функциональных интегралов. Одним из плюсов последнего метода является отсутствие проблем некоммутативности операторов поля и разного рода упорядочиваний.

Операторный подход

Определение температурных функций Грина

Введём мацубаровские $\hat{\mathrm{\Psi }}$ — операторы в «гейзенберговском представлении» соотношениями:

$\hat{\mathrm{\Psi }}(\tau ,𝐫)=e^{\tau (\hat{H}-\mu \hat{N})}\hat{\psi }(𝐫)e^{-\tau (\hat{H}-\mu \hat{N})},$ ${\hat{\mathrm{\Psi }}}^{†}(\tau ,𝐫)=e^{\tau (\hat{H}-\mu \hat{N})}\hat{\psi }(𝐫{)}^{+}{e}^{-\tau (\hat{H}-\mu \hat{N})}.$

В более общем случае эти операторы могут иметь спиновые индексы. В этих формулах $\tau$ — вещественная переменная $\tau \in (0,1/T)$, поэтому операторы $\hat{\mathrm{\Psi }}(\tau ,𝐫)$ и ${\hat{\mathrm{\Psi }}}^{†}(\tau ,𝐫)$ не являются эрмитово-сопряженными, $\mu$ — химический потенциал системы, $\hat{H}$ — гамильтониан системы, $\hat{N}=\int d𝐫{\hat{\psi }}^{+}(𝐫)\hat{\psi }(𝐫)$ — оператор числа частиц. Операторы $\hat{\psi }(𝐫)$ и ${\hat{\psi }}^{+}(𝐫)$ эрмитово-сопряженный операторы поля в шрёденгеровском представлении. Видно, что «гейзенберговское представление» мацубаровских операторов отличается от настоящего гейзенберговского представления заменой в последнем $t\to -i\tau$, то есть формально это можно понимать как переход ко мнимому времени. Температурная функция Грина определяется следующим образом:

$G(\tau ,{𝐫}_1;{\tau }^{\prime },{𝐫}_2)=-\frac{Tr\{e^{\frac{(\hat{H}-\mu \hat{N})}{T}}{T}_{\tau }{\hat{\mathrm{\Psi }}}^{†}(\tau ,{𝐫}_1)\hat{\mathrm{\Psi }}({\tau }^{\prime },{𝐫}_2)\}}{Tr\left\{e^{\frac{(\hat{H}-\mu \hat{N})}{T}}\right\}},$

где символ $T_{\tau }$ означает «$\tau$ — хронологизацию» — расположение операторов слева на право в порядке убывания $\tau$. В случае ферми-частиц перестановка между собой операторов приводит к изменению общего знака. С помощью этой функции можно вычислить число частиц как функцию химического потенциала, или химический потенциал, как функцию концентрации и температуры: $N=\pm \int d𝐫G(\tau ,𝐫;\tau +0,𝐫).$

Случай свободных частиц

Гамильтониан свободной системы, выраженный через шрёдингеровские операторы поля, имеет вид:

$\widehat{H_0}=\int \hat{\psi }(𝐫{)}^{+}(-\frac{\mathrm{\Delta }}{2m})\hat{\psi }(𝐫)d𝐫,$

в представлении вторичного квантования он же запишется следующим образом:

$\widehat{H_0}=\sum {\epsilon }_0(𝐩){\hat{a}}_{𝐩}^{+}{\hat{a}}_{𝐩},{\epsilon }_0(𝐩)=p^2/2m,$

что следует из определения $\hat{\psi }$-операторов:

$\hat{\psi }(𝐫)=\frac{1}{\sqrt{V}}\sum e^{i𝐩𝐫}{\hat{a}}_{𝐩},\hat{\psi }(𝐫{)}^{+}=\frac{1}{\sqrt{V}}\sum e^{-i𝐩𝐫}{\hat{a}}_{𝐩}^{+}.$

Температурная функция Грина свободных частиц в импульсно-«временном» представлении :

$G(𝐩,\tau ,{\tau }^{\prime })=e^{{\xi }_0(𝐩)(\tau -{\tau }^{\prime })}(\mathrm{\Theta }({\tau }^{\prime }-\tau )\mp \frac{1}{e^{{\xi }_0(𝐩)\beta }\pm 1}),$

здесь ${\xi }_0(𝐩)={\epsilon }_0(𝐩)-\mu ,\beta =1/T.$

Взаимодействующие частицы

Предположим, что на систему частиц не действуют внешние поля, а межчастичные взаимодействия носят парный характер. Гамильтониан системы представим в виде: $\hat{H}={\hat{H}}_0+{\hat{H}}_{int}.$ Введём мацубаровские операторы в представлении взаимодействия соотношениями:

$\hat{\mathrm{\Phi }}(\tau ,𝐫)=e^{\tau ({\hat{H}}_0-\mu \hat{N})}\hat{\psi }(𝐫)e^{-\tau ({\hat{H}}_0-\mu \hat{N})},$ ${\hat{\mathrm{\Phi }}}^{†}(\tau ,𝐫)=e^{\tau ({\hat{H}}_0-\mu \hat{N})}\hat{\psi }(𝐫{)}^{+}{e}^{-\tau ({\hat{H}}_0-\mu \hat{N})}.$

Возмущённая часть гамильтониана выраженный через $\hat{\mathrm{\Phi }}$ — операторы имеет вид:

${\hat{H}}_{int}=\frac{1}{2}\int \int d{𝐫}_{\mathrm{𝟏}}d{𝐫}_{\mathrm{𝟐}}\hat{\mathrm{\Phi }}({𝐫}_{\mathrm{𝟏}},\tau ){\hat{\mathrm{\Phi }}}^{†}({𝐫}_{\mathrm{𝟏}},\tau )U({𝐫}_{\mathrm{𝟏}}-{𝐫}_{\mathrm{𝟐}})\hat{\mathrm{\Phi }}({𝐫}_{\mathrm{𝟐}},\tau ){\hat{\mathrm{\Phi }}}^{†}({𝐫}_{\mathrm{𝟐}},\tau ).$

Через эти же операторы можно определить температурную функцию Грина:

$G({\tau }_1,{𝐫}_1;{\tau }_2,{𝐫}_2)=-\frac{Tr\{e^{({\hat{H}}_0-\mu \hat{N})\beta }{T}_{\tau }\hat{\mathrm{\Phi }}({\tau }_1,{𝐫}_1){\hat{\mathrm{\Phi }}}^{†}({\tau }_2,{𝐫}_2)S(\beta )\}}{Tr\{e^{\frac{({\hat{H}}_0-\mu \hat{N})}{T}}S(\beta )\}},$ $S(\beta )=T_{\tau }\exp (-\underset{0}{\overset{\beta }{\int }}{\hat{H}}_{int}(\tau )d\tau ).$

Такая запись позволяет разложить экспоненту с возмущением и вычислять температурную функцию Грина в виде ряды, а каждый член ряда изображать графически в виде диаграммы.

Правила температурной диаграммной техники. Координатное представление.

	Элементы Диаграммы		Аналитическое выражение
	название	изображение
1	Сплошная линия		$G_0({𝐫}_1-{𝐫}_2,{\tau }_1-{\tau }_2)$
2	Сплошная линия		$G_0({𝐫}_2-{𝐫}_1,{\tau }_2-{\tau }_1)$
3	Волнистая линия		$𝔘(x_1-x_2)=U({𝐫}_1-{𝐫}_2)\delta ({\tau }_1-{\tau }_2)$
4	Изобразить все связные топологически неэквивалентные диаграммы с 2n вершинами и двумя внешними концами, причем в каждой вершине сходится две сплошные и одна волнистая линия.
5	Производится интегрирование по координатам ($d^{4}z=d𝐫d\tau$) каждой вершины.
6	Полученное выражение умножается на $(-1{)}^{n+F}$, n-порядок диаграммы, F-число замкнутых фермионных петель в ней.

Пользуясь этими правилами изобразим поправку первого порядка по возмущению к температурной функции Грина взаимодействующих частиц. Для этого нужно ограничиться линейным членом в разложение экспоненты. Тогда, привлекая во внимание теорему Вика, нарисуем все связные (любые две точки на диаграмме можно соединить линией) диаграммы первого порядка:

gren1

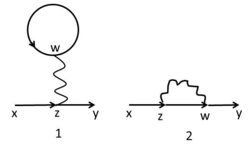
Соответствующее аналитическое выражение, например, для диаграммы 2 запишется следующим образом:

$Dia{g}_2(x-y)=-\iint d^{4}z{d}^{4}w{G}_0(x-z)G_0(z-w)G_0(w-y)𝔘(z-w).$

Для расчётов координатное представление оказывается неудобным, поэтому всю диаграммную технику проще сформулировать в импульсно-частотном представлении, пользуясь обычными правилами фурье-анализа. В таком представлении аналитическое выражение рассматриваемой диаграммы примет вид:

$Dia{g}_2(𝐩,{\omega }_n)=-\frac{T}{(2\pi {)}^3}\sum _{{\omega }_m}\int d{𝐩}_1{G}_0^2(𝐩,{\omega }_n)G_0({𝐩}_1,{\omega }_m)𝔘(𝐩-{𝐩}_1,{\omega }_n-{\omega }_m),$

где функция Грина свободной системы имеет вид:

$G_0(𝐩,{\omega }_n)=\frac{1}{i{\omega }_n-{\epsilon }_0(𝐩)+\mu },$ ${\omega }_n=(2n+1)\pi T$ — для фермионов, ${\omega }_n=2n\pi T$ — для бозонов.

Правила температурной диаграммной техники. Импульсно-частотное представление.

	Элементы Диаграммы		Аналитическое выражение
	название	изображение
1	Сплошная линия		$G_0(𝐩,{\omega }_n)$
3	Волнистая линия		$𝔘(𝐩,{\omega }_n)=U(𝐩)$
4	Сопоставить линиям диаграммы внешние импульсы и частоты. Импульсы и частоты внутренних линий в каждой вершине должны удовлетворять законам сохранения $\sum 𝐩=0,\sum \omega =0$
5	По всем независимым импульсам производится интегрирование, по частотам — суммирование.
6	Полученное выражение умножается на $(-1{)}^k\frac{T^k}{(2\pi {)}^{3k}}(2s+1{)}^F(\mp {)}^F$, k-порядок диаграммы, F-число замкнутых петель в диаграмме, s — спин частицы.

В простейшем случае (Л.Ландау) потенциал можно взять в виде $U({𝐫}_1-{𝐫}_2)\sim \delta ({𝐫}_1-{𝐫}_2),,$ что соответствует нулевому радиусу взаимодействия. Графически это соответствует стягиванию двух точек, которые соединены волнистой линией в одну.

Метод функционального интегрирования

При переходе от классической статистической механики к квантовой, интегрирование по канонически сопряженным переменным $p,q$ заменяется на след, то есть на сумму по состояниям. Таким образом, статистическая сумма квантовой системы с оператором Гамильтона $\hat{H}$ определяется как

$Z=Tr{e}^{-\beta \hat{H}}=\sum _n⟨n|e^{-\beta \hat{H}}|n⟩.$

Видно, что член под знаком суммы похож на матричный элемент оператора эволюции с точностью до замены $t\to -i\beta$. Этот матричный элемент дается формулой Фейнмана-Каца:

$⟨q_2|e^{-it\hat{H}}|q_1⟩=\int \prod _t\frac{dp(t)dq(t)}{2\pi }\exp \left(i\underset{0}{\overset{t}{\int }}(p\dot{q}-H(p,q))dt\right).$

Обратим внимание на то, что в функциональном интеграле величины $p,q,H(p,q)$ являются классическими функциями, и при дальнейших вычислениях не возникает проблемы с коммутационными соотношениями. Сделаем в этой формуле поворот Вика и отождествим $q\sim \psi (x,\tau ),p\sim i{\psi }^{+}(x,\tau )$, тогда выражений для статистической суммы преобразится к виду:

$Z=\underset{B.C.}{\int }𝒟\psi 𝒟{\psi }^{+}{e}^{-S_{\beta }},B.C.=\{\begin{array}{cc}\psi (x,\tau )=\psi (x,\tau +\beta ),& \text{Bose}\\ \psi (x,\tau )=-\psi (x,\tau +\beta ),& \text{Fermi}\end{array},$

где $S_{\beta }$ действие температурной теории, интегрирование ведётся по полям с соответствующими граничными условиями (B.C.) В случае идеального газа

$S_{\beta }^0=\underset{0}{\overset{\beta }{\int }}d\tau \int d𝐱{\psi }^{+}(x,\tau )({\partial }_{\tau }+\frac{\mathrm{\Delta }}{2m}-\mu )\psi (x,\tau ).$

Парное взаимодействие можно учесть в виде члена типа плотность-плотность

$S_{\beta }^{int}=\frac{1}{2}\underset{0}{\overset{\beta }{\int }}d\tau \int d𝐱d{𝐱}^{\prime }{\psi }^{+}(x,\tau )\psi (x,\tau )U(𝐱-{𝐱}^{\prime }){\psi }^{+}(x^{\prime },\tau )\psi (x^{\prime },\tau ).$

Как было сказано выше объекты $\psi (x,\tau ),{\psi }^{+}(x,\tau )$ не являются полевыми операторами. В случае фермионов они являются грассмановыми функциями, что является наследием антисимметричности фермионных волновых функций.

Определение температурной функции Грина

Определим функцию Грина как среднее от произведения нескольких полей с весом $\exp (-S_{\beta })$. Так парная корреляционная функция даётся выражением

$G(x,x^{\prime },\tau ,{\tau }^{\prime })=⟨{\psi }^{+}(x,\tau )\psi (x^{\prime },{\tau }^{\prime })⟩=\frac{1}{Z}\underset{B.C.}{\int }𝒟\psi 𝒟{\psi }^{+}{\psi }^{+}(x,\tau )\psi (x^{\prime },\tau )e^{-S_{\beta }},S_{\beta }=S_{\beta }^0+S_{\beta }^{int}.$

Для корректного определения этого объекта, как можно показать, нужно доопределение $G(x,x^{\prime },\tau ={\tau }^{\prime })=G(x,x^{\prime },\tau ={\tau }^{\prime }+0).$

Случай свободных частиц

Вычислим функцию Грина для невзаимодействующих частиц. Как известно, для этого нужно найти ядро оператора ${(-{\partial }_{\tau }+{\hat{H}}_1)}^{-1}$ c учётом граничных условий, то есть решить уравнение

$(-{\partial }_{\tau }+{\hat{H}}_1)G_0(x,x^{\prime },\tau ,{\tau }^{\prime })=\delta (x-x^{\prime })\delta (\tau -{\tau }^{\prime }).$

Уравнение элементарно решается в $p-\tau$ представлении

$G_0(𝐩,\tau ,{\tau }^{\prime })=e^{{\xi }_0(𝐩)(\tau -{\tau }^{\prime })}(\mathrm{\Theta }({\tau }^{\prime }-\tau )\mp \frac{1}{e^{{\xi }_0(𝐩)\beta }\pm 1}).$

Как видно, эта функция Грина совпадает с функцией Грина полученной с помощью мацубаровских операторов. Доопределение этой функции при совпадающих «временах» означает, что тета-функция в нуле равна нулю.

Взаимодействующие частицы

Рассмотрим, например, бозоны с межчастичным взаимодействием типа $U(x-x^{\prime })=\lambda \delta (x-x^{\prime }),\lambda >0.$ Для вычисления по теории возмущений разложим экспоненту со взаимодействием в ряд по параметру $\lambda$ и для простоты ограничимся первым порядком

$⟨{\psi }^{+}(x,\tau )\psi (x^{\prime },{\tau }^{\prime })⟩={⟨{\psi }^{+}(x,\tau )\psi (x^{\prime },{\tau }^{\prime })⟩}_0-\frac{\lambda }{2}\underset{0}{\overset{\beta }{\int }}dt\int d𝐲{⟨{\psi }^{+}(x,\tau )\psi (x^{\prime },{\tau }^{\prime }){({\psi }^{+}(y,\tau )\psi (y,\tau ))}^2⟩}_0+O({\lambda }^2).$

Построим соответствующую диаграммную технику

Правила температурной диаграммной техники. Координатное представление.

	Элементы Диаграммы		Аналитическое выражение
	название	изображение
1	Крест		${\psi }^{+}(x,\tau )$
2	Точка		$\psi (x,\tau )$
3	Пропагатор		${⟨{\psi }^{+}(x,\tau )\psi (x^{\prime },{\tau }^{\prime })⟩}_0=G_{+,0}(x,x^{\prime },\tau ,{\tau }^{\prime })$
4	Пропагатор		${⟨\psi (x^{\prime },{\tau }^{\prime }){\psi }^{+}(x,\tau )⟩}_0=G_{0,+}(x^{\prime },x,{\tau }^{\prime },\tau )$
3	Вершина		${({\psi }^{+}(x,\tau )\psi (x,\tau ))}^2$
5	Домножить каждую вершину на $(-\lambda /2{)}^{n}r/n!$, где n-порядок диаграммы, r-симметрийный коэффициент-число топологически эквивалентных графов.
5	По всем координатам вершин производится интегрирование.

Изобразим в первом порядке все связные графы

graph+

.

Существует только одна диаграмма, для неё $r=4$. Соответствующее аналитическое выражение для поправки

$Diag=-2\lambda \underset{0}{\overset{\beta }{\int }}dt\int dy{G}_{+,0}(x,y,\tau ,t)G_{+,0}(y,y,t,t)G_{+,0}(y,x^{\prime },t,{\tau }^{\prime }),$

это выражение в точности совпадает с полученным ранее в операторном методе. Для рассматриваемого потенциала две диаграммы 1 и 2 становятся эквивалентными, поэтому для получения однопетлевого вклада, нужно выражение для одной из диаграмм умножить на 2. Конечно и в этом случае разумно перейти в импульсное представление. Правила построения диаграмм в импульсном представлении здесь такие же, как и ранее.

Литература

• Шаблон:Книга
• Шаблон:Книга
• Шаблон:Книга

См. также

• Квантовополевая теория возмущений в статистической физике
• Критические явления
• Квантовый газ
• Квантовая теория поля
• Функциональный интеграл
• Статистическая физика
• Теория Ландау
• Теорема Вика для функционального интеграла