Правильная карта (теория графов)

Правильная карта — это симметричное замощение замкнутой поверхности. Более точно, правильная карта — это Шаблон:Не переведено 5 двумерного многообразия (такого как сфера, тор или вещественная проективная плоскость) на топологические диски, так что каждый флаг (инцидентная тройка вершина-ребро-грань) может быть переведён в любой другой флаг преобразованием симметрии разложения. Правильные карты являются в некотором смысле топологическим обобщением правильных многогранников. Теория карт и их классификация связана с теориями римановых поверхностей, геометрии Лобачевского и теории Галуа. Правильные карты классифицируются по их роду ориентируемости соответствующей поверхности, по основному графу или автоморфизму группы.

Обзор

Правильные карты обычно определяются и изучаются тремя способами: топологически, с точки зрения теории групп и теории графов.

Топологический подход

С точки зрения топологии карта является 2-ячейным разложением замкнутого компактного 2-многообразия.

Род g карты M задаётся соотношением Эйлера $χ (M) = | V | - | E | + | F |$ , что равно $2 - 2 g$ , если карта ориентируема, и $2 - g$ , если карта неориентируема. Критическим обстоятельством является факт, что имеется конечное (ненулевое) число правильных карт для любого ориентируемого рода, за исключением тора.

Подход теории групп

С точки зрения теории групп перестановки представления правильной карты M являются транзитивной группой перестановок C на множестве $Ω$ флагов, порождённой свободными инволюциями с тремя фиксированными точками $r_{0}, r_{1}, r_{2}$ , удовлетворяющими условию $(r_{0} r_{2})^{2} = I$ . В этом определении гранями являются орбиты $F = ⟨ r_{0}, r_{1} ⟩$ , рёбрами являются орбиты $E = ⟨ r_{0}, r_{2} ⟩$ , а вершинами являются орбиты $V = ⟨ r_{1}, r_{2} ⟩$ . Более абстрактно, автоморфизм группы любой правильной карты является невырожденным гомоморфным образом группы треугольника <2,m,n>.

Подход теории графов

С точки зрения теории графов карта есть кубический граф $Γ$ с рёбрами, выкрашенными в синий, жёлтый и красный цвета так, что $Γ$ связен, каждая вершина инцидентна с рёбрами каждого цвета, а циклы рёбер, не окрашенных в жёлтый цвет, имеют длину 4. Заметим, что $Γ$ является плоским графом или Шаблон:Не переведено 5 (Шаблон:Lang-en, GEM) карты, определёнными на множестве флагов в качестве вершин $Ω$ и не являющимися остовом G=(V,E) карты. В общем случае $| Ω | = 4 | E |$ .

Карта M правильна тогда и только тогда, когда Aut(M) действует регулярно на флаги. Aut(M) правильной карты транзитивна на вершинах, рёбрах и гранях карты M. Говорят, что карта M зеркально симметрична в том и только в том случае, когда Aut(M) правильна и содержит автоморфизм $ϕ$ , который фиксирует как вершиныv, так и грани f, но обращает направление рёбер. Говорят, что правильная карта, не являющаяся зеркально симметричной, хиральна.

Примеры

Большой додекаэдр является правильной картой с пятиугольными гранями на ориентируемой поверхности рода 4.
Шаблон:Не переведено 5 является правильной картой типа {4,3} на проективной плоскости.
Полудодекаэдр является правильной картой, порождённой пятиугольным вложением графа Петерсена в проективную плоскость.
p-Осоэдр является правильной картой типа {2,p}. Заметим, что осоэдры в этом смысле не являются абстрактными многогранниками. В частности, они не удовлетворяют свойству алмаза (Шаблон:Lang-en).
Карта Дика является правильной картой из 12 октаэдров на поверхности рода 3. Лежащий в её основе граф Дика, может также образовать правильную карту из 16 шестиугольников на торе.

В таблице ниже приведён полный список правильных карт на поверхностях с положительной эйлеровой характеристикой, χ — сфере и проективной плоскостиШаблон:Sfn.

χ	g	Шлефли	Вершин	Рёбер	Граней	Группа	Порядок	Граф	Примечания
2	0	{p,2}	p	p	2	C₂ × Dih_p	4p	C_p	Диэдр
2	0	{2,p}	2	p	p	C₂ × Dih_p	4p	p-кратный K₂	Осоэдр
2	0	{3,3}	4	6	4	S₄	24	K₄	Тетраэдр
2	0	{4,3}	8	12	6	C₂ × S₄	48	K₄ × K₂	Куб
2	0	{3,4}	6	12	8	C₂ × S₄	48	K_2,2,2	Октаэдр
2	0	{5,3}	20	30	12	C₂ × A₅	120		Додекаэдр
2	0	{3,5}	12	30	20	C₂ × A₅	120	K₆ × K₂	Икосаэдр
1	n1	{2p,2}/2	p	p	1	Dih_2p	4p	C_p	ПолудиэдрШаблон:R
1	n1	{2,2p}/2	2	p	p	Dih_2p	4p	p-кратный K₂	ПолуосоэдрШаблон:R
1	n1	{4,3}/2	4	6	3	S₄	24	K₄	Шаблон:Не переведено 5
1	n1	{3,4}/2	3	6	4	S₄	24	2-кратный K₃	Шаблон:Не переведено 5
1	n1	{5,3}/2	10	15	6	A₅	60	Граф Петерсена	Полудодекаэдр
1	n1	{3,5}/2	6	15	10	A₅	60	K₆	Полуикосаэдр

Изображения ниже показывают три из 20 правильных карт в Шаблон:Не переведено 5 с их символами Шлефли.

{6,4}
{4,8}
{8,4}

Тороидальные многогранники

Примеры в виде мозаики
{4,4}_1,0 (v:1, e:2, f:1)	{4,4}_1,1 (v:2, e:4, f:2)	{4,4}_2,0 (v:4, e:8, f:4)	{4,4}_2,1 (v:5, e:10, f:5)	{4,4}_2,2 (v:8, e:16, f:8)
{3,6}_1,0 (v:1, e:3, f:2)	{3,6}_1,1 (v:3, e:9, f:6)	{3,6}_2,0 (v:4, e:8, f:8)	{3,6}_2,1 (v:7, e:21, f:14)	{3,6}_2,2 (v:12, e:36, f:24)
{6,3}_1,0 (v:2, e:3, f:1)	{6,3}_1,1 (v:6, e:9, f:3)	{6,3}_2,0 (v:8, e:8, f:4)	{6,3}_2,1 (v:14, e:21, f:7)	{6,3}_2,2 (v:24, e:36, f:12)

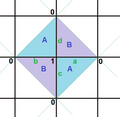
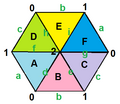
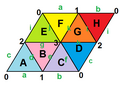
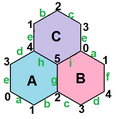
Правильные карты существуют как тороидальные многогранники в виде конечных порций евклидовых мозаик, завёрнутых в поверхность Шаблон:Нп5 как плоского тора. Они помечены как {4,4}_b,c, когда они связаны с квадратной мозаикой {4,4}Шаблон:Sfn, как ${3, 6}_{b, c}$ , когда они связаны с треугольной мозаикой {3,6}, и как {6,3}_b,c, когда связаны с шестиугольной мозаикой {6,3}. Индексы b и c являются целыми числами Шаблон:Sfn. Имеется 2 специальных случая (b,0) и (b,b) с зеркальной симметрией, хотя общие случаи существуют в хиральных парах (b,c) и (c,b).

Правильные карты вида {4,4}_m,0 могут быть представлены как конечные правильные косые многогранники {4,4|m}, понимаемые как квадратные грани m×m дуопризмы в размерности 4.

Ниже приведён пример {4,4}_8,0, отображённый из плоского листа в виде шахматной доски в цилиндр, а затем в тор. Проекция из цилиндра в тор искажает геометрию в трёхмерном пространстве, но может быть осуществлена без искажения в четырёхмерном.

Правильные карты с нулевой эйлеровой характеристикой Шаблон:Sfn
g	Шлефли	Вершин	Рёбер	Граней	Группа	Порядок	Примечания
1	{4,4}_b,0 n=b²	n	2n	n	[4,4]_(b,0)	8n	Плоский тороидальный многогранник То же, что и {4,4 \| b}
1	{4,4}_b,b n=2b²	n	2n	n	[4,4]_(b,b)	8n	Плоский тороидальный многогранник То же, что и полноусечённый {4,4 \| b}
1	{4,4}_b,c n=b²+c²	n	2n	n	[4,4]Шаблон:Supsub	4n	Плоский хиральный тороидальный многогранник
1	{3,6}_b,0 t=b²	t	3t	2t	[3,6]_(b,0)	12t	Плоский тороидальный многогранник
1	{3,6}_b,b t=2b²	t	3t	2t	[3,6]_(b,b)	12t	Плоский тороидальный многогранник
1	{3,6}_b,c t=b²+bc+c²	t	3t	2t	[3,6]Шаблон:Supsub	6t	Плоский хиральный тороидальный многогранник
1	{6,3}_b,0 t=b²	2t	3t	t	[3,6]_(b,0)	12t	Плоский тороидальный многогранник
1	{6,3}_b,b t=2b²	2t	3t	t	[3,6]_(b,b)	12t	Плоский тороидальный многогранник
1	{6,3}_b,c t=b²+bc+c²	2t	3t	t	[3,6]Шаблон:Supsub	6t	Плоский хиральный тороидальный многогранник

В общем случае правильный тороидальный многогранник {p,q}_b,c можно определить, если p или q чётные, хотя только один евклидов выше может существовать как тороидальный многогранник в размерности 4. В случае {2p,q} пути (b,c) можно определить как грань-ребро-грань на прямой, в то время как в двойственных {p,2q} формах пути (b,c) можно рассматривать как вершина-ребро-вершина.

См. также

Примечания

Шаблон:Примечания

Литература

Шаблон:Refbegin

Шаблон:Refend Шаблон:Rq

Правильная карта (теория графов)

Содержание

Обзор

Топологический подход

Подход теории групп

Подход теории графов

Примеры

Тороидальные многогранники

См. также

Примечания

Литература

Навигация

Правильная карта (теория графов)

Обзор

Топологический подход

Подход теории групп

Подход теории графов

Примеры

Тороидальные многогранники

См. также

Примечания

Литература

Навигация

Поиск