Парабола

Шаблон:Другие значения Шаблон:Карточка Пара́бола (Шаблон:Lang-el — приближение) — плоская кривая, один из типов конических сечений.

Определение

Античные математики определяли параболу как результат пересечения кругового конуса с плоскостью, которая не проходит через вершину конуса и параллельна его образующей (см. рисунок). В аналитической геометрии удобнее эквивалентное определение: парабола есть геометрическое место точек на плоскости, для которых расстояние до заданной точки (фокуса) равно расстоянию до заданной прямой (директрисы) (см. рисунок)Шаблон:Sfn.

Если фокус лежит на директрисе, то парабола вырождается в прямую.

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Парабола в семействе конических сечений

Вершина

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

Уравнения

Каноническое уравнение параболы в прямоугольной системе координат:

$y^2=2px,p>0$ (или $x^2=2py$, если поменять местами оси координат).

Число Шаблон:Math называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии $\frac{p}{2}$ от обоих.

Вывод

Уравнение директрисы PQ: $x+\frac{p}{2}=0$, фокус F имеет координаты $(\frac{p}{2};0).$ Таким образом, начало координат O — середина отрезка CF. По определению параболы, для любой точки M, лежащей на ней, выполняется равенство Шаблон:Nobr. Далее, поскольку $\text{KM=KD+DM}=\frac{p}{2}+x$ и $\text{FM}=\sqrt{{(x-\frac{p}{2})}^2+y^2}$, то равенство приобретает вид: $\sqrt{{(x-\frac{p}{2})}^2+y^2}=\frac{p}{2}+x.$ После возведения в квадрат и некоторых преобразований получается равносильное уравнение $y^2=2px.$

Парабола, заданная квадратичной функцией

Файл:Parabola with Processing.webm Квадратичная функция $y=a{x}^2+bx+c$ при $a\ne 0$ также является уравнением параболы и графически изображается той же параболой, что и $y=a{x}^2,$ но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

$x_{\text{A}}=-\frac{b}{2a},y_{\text{A}}=-\frac{𝒟}{4a},$ где $𝒟=b^2-4ac$ — дискриминант квадратного трёхчлена.

Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При Шаблон:Math (Шаблон:Math) фокус лежит на этой оси над (под) вершиной на расстоянии 1/4Шаблон:Math, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение $y=a{x}^2+bx+c$ может быть представлено в виде $y=a(x-x_{\text{A}}{)}^2+y_{\text{A}},$ а в случае переноса начала координат в точку A уравнение параболы превращается в каноническое. Таким образом, для каждой квадратичной функции можно найти систему координат такую, что в этой системе уравнение соответствующей параболы представляется каноническим. При этом $p=\frac{1}{|2a|}.$

Общее уравнение параболы

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

$A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0.$

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант $B^2-4AC$ равен нулю.

Уравнение в полярной системе

Парабола в полярной системе координат $(\rho ,\vartheta )$ с центром в фокусе и нулевым направлением вдоль оси параболы (от фокуса к вершине) может быть представлена уравнением

$\rho (1-\cos \vartheta )=p,$

где Шаблон:Math — фокальный параметр (расстояние от фокуса до директрисы или удвоенное расстояние от фокуса до вершины)

Уравнение в подерной системе

Парабола в подерной системе координат $(r,p)$ с центром в фокусе и параметром $a$, равным расстоянию от фокуса до вершины параболы, может быть представлена следующим уравнениемШаблон:Sfn:

$p^2=ar.$

Расчёт коэффициентов квадратичной функции

Если для уравнения параболы с осью, параллельной оси ординат, $y=a{x}^2+bx+c$ известны координаты трёх различных точек параболы $(x_1;y_1),(x_2;y_2),(x_3;y_3),$ то его коэффициенты могут быть найдены так:

$a=\frac{y_3-\frac{x_3(y_2-y_1)+x_2{y}_1-x_1{y}_2}{x_2-x_1}}{x_3(x_3-x_1-x_2)+x_1{x}_2},b=\frac{y_2-y_1}{x_2-x_1}-a(x_1+x_2),c=\frac{x_2{y}_1-x_1{y}_2}{x_2-x_1}+a{x}_1{x}_2.$

Если же заданы вершина $(x_0;y_0)$ и старший коэффициент $a$, то остальные коэффициенты и корни вычисляются по формулам:

$b=-2a{x}_0$

$c=a{x}_0^2+y_0$

$x_1=x_0+\sqrt{-\frac{y_0}{a}}$

$x_2=x_0-\sqrt{-\frac{y_0}{a}}$

Свойства

Отражательное свойство параболы (оптика)

Расстояние от Шаблон:Math до фокуса Шаблон:Math такое же, как и от Шаблон:Math до Шаблон:Math (на директрисе L)

Длина линий Шаблон:Math одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
• Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. Сигнал также придет в одной фазе, что важно для антенн.
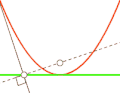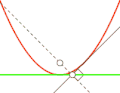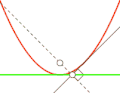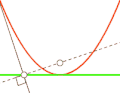
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Множество всех точек, из которых парабола видна под прямым углом, есть директриса.
• Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
• Парабола является антиподерой прямой.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• Траектория фокуса параболы, катящейся по прямой, есть цепная линия.
• Описанная окружность треугольника, описанного около параболы, проходит через её фокус, а точка пересечения высот лежит на её директрисе

Связанные определения

• При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Подера параболы

Шаблон:Обзорная статья Любая парабола имеет подеру — циркулярную кривую 3-го порядка на комплексной проективной плоскостиШаблон:Sfn.

• Подеры параболы
• 
  Прямая — полюс подеры в фокусе параболы
• 
  Циссоида Диокла — полюс подеры на вершине параболы
• 
  Строфоида $(y+1)(x^2+y(y+1))+x^2=0$ — полюс подеры в центре директрисы параболы $x^2=4y$
• 
  Офиурида $(y+1)(x(x-2)+y(y+1))+(x-2{)}^2=0$ — полюс подеры не в центре директрисы параболы $x^2=4y$
• 
  Прямая конхоида Слюза $(y-4)(x^2+y(y-4))+x^2=0$ — полюс подеры внутри на оси не в фокусе параболы $x^2=4y$
• 
  Конхоида Слюза $(y-4)(x(x-2)+y(y-4))+(x-2{)}^2=0$ — полюс подеры внутри не на оси параболы $x^2=4y$

Не умаляя общности, уравнение произвольной параболы можно записать в следующем видеШаблон:Sfn:

$y^2=4px,$ или $x^2=4py,$

где $p$ — расстояние от фокуса параболы до её вершины и от вершины до директрисы.

Тогда подера произвольной параболы $y^2=4px$ относительно произвольного полюса $(a,b)$ есть дефективная гипербола с двойной точкой $(a,b)$, асимптотой $a-p$ и следующим уравнениемШаблон:SfnШаблон:Sfn:

$(x-a)(y(y-b)+x(x-a))+p(y-b{)}^2=0.$

Другими словами, имеет место следующее утверждениеШаблон:Sfn:

подера параболы — это рациональная циркулярная кривая 3-го порядка.

Имеют место три разных случая, в которых дефективная гипербола выступает тремя разными частными случаямиШаблон:SfnШаблон:Sfn:

• полюс подеры находится на параболе. Тогда полюс — точка возврата подеры;

• если полюс лежит на касательной к вершине параболы, то подера — офиуридаШаблон:Sfn;

• если полюс совпадает с вершиной параболы, то подера — циссоида;

• полюс подеры находится во внешности параболы. Тогда полюс — узловая точка подеры;

• в частности, если полюс находится на директрисе параболы, то подера — строфоида;

• полюс подеры находится внутри параболы. Тогда полюс — мнимая изолированная точка подеры;

• если полюс лежит на оси симметрии параболы, но не совпадает с фокусом параболы, то подера — конхоида СлюзаШаблон:Sfn;
• если полюс совпадает с фокусом параболы, то подера состоит из трёх прямых на комплексной проективной плоскости:

• действительной прямой, которая касается параболы в её вершине;
• две мнимые прямые, которые пересекаются в фокусе параболы.

Вариации и обобщения

Графики степенной функции $y=x^n$ при натуральном показателе $n>1$ называются параболами порядка $n$. Ранее рассмотренное определение соответствует $n=2,$ то есть параболе 2-го порядка.

Парабола также представляет собой синусоидальную спираль при $n=-\frac{1}{2}$;

Параболы в физическом пространстве

Параболический компас Леонардо да Винчи

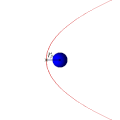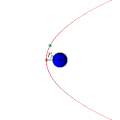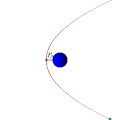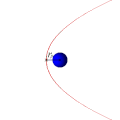
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).

Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассегрена, Шмидта — Кассегрена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

• 
  Параболическая орбита и движение спутника по ней (анимация)
• 
  Падение баскетбольного мяча
• 
  Параболическая солнечная электростанция в Калифорнии, США
• 
  Параболические траектории струй воды
• 
  Вращающийся сосуд с жидкостью
• 
  Парабола — антиподера прямой

Литература

• Шаблон:Книга
• Шаблон:Статья
• Шаблон:Книга
• Шаблон:Книга
• Шаблон:H
• Шаблон:H
• Шаблон:H

Ссылки

• Статья в справочнике «Прикладная математика».
• Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
• Информация (англ.) о связи параболы с физикой.
• Учебный фильм о параболе