Молекулярная симметрия

Молекулярная симметрия — это фундаментальная концепция химии, описывающая и классифицирующая симметрию молекулы, используемая для предсказания или объяснения химических свойств молекул. Например, таких как дипольный момент и разрешённые спектроскопические переходы. Изучение молекулярной симметрии основано на теории групп. Состояние молекулы классифицируется с помощью неприводимых представлений из таблицы характеров группы симметрии молекулы.
Симметрия используется при изучении молекулярных орбиталей с приложениями, такими как Шаблон:Нп5, Шаблон:Нп5 и правила Вудворда — Хофмана. Другой базой в больших масштабах является использование кристаллических систем для описания кристаллографической симметрии. Молекулярная симметрия — один из факторов, определяющих свойства материалов в кристалохимии.
Существует много методов установления симметрии молекулы, включая рентгеноструктурный анализ и различные формы спектроскопии. Шаблон:Нп5 основываются на симметрии.
Концепции симметрии
Для изучения молекулярной симметрии используется теория групп.
| Ось вращения () | Несобственные элементы вращения () | ||
|---|---|---|---|
| Хиральная нет |
Ахиральная плоскость отражения |
Ахиральная центр симметрии | |
 |
 |

| |
 |
 |

| |
Элементы симметрии
Точечная группа симметрии молекулы может быть описана пятью типами Шаблон:Нп5. Шаблон:Anchor
- Ось симметрии: ось, вокруг которой вращение на приводит к молекуле, неотличимой от исходной. Она называется также n-кратной осью вращения и обозначается . Примерами являются ось в молекуле воды и ось в молекуле аммиака. Молекула может иметь более одной оси симметрии. Ось с высшим n называется главной осью и по соглашению она располагается вдоль оси z декартовой системы координат.
- Плоскость симметрии - плоскость, при отражении относительно которой получается идентичная копия исходной молекулы. Она называется также плоскостью отражения и обозначается как (сигма = греческое «с», имеется ввиду немецкое слово «Spiegel», что значит «зеркало», но буква S занята другим видом симметрии — см. ниже)Шаблон:R. Вода имеет две плоскости симметрии — одна в плоскости молекулы и одна перпендикулярна ей. Плоскость симметрии, параллельная главной оси, называется вертикальной (), а перпендикулярная ей называется горизонтальной (). Существует третий тип плоскостей симметрии — если вертикальная плоскость симметрии кроме того делит пополам угол между двумя 2-кратными осями вращения, перпендикулярными главной оси, плоскость называется двугранной (). Плоскость симметрии может быть определена по её декартовой ориентации, например, (xz) или (yz).
- Центр симметрии - обозначается как i (от английского «inversion center»). Молекула имеет центр симметрии, если для любого атома в молекуле имеется атом, диаметрально противоположный относительно центра и располагающийся на том же расстоянии от него. Другими словами, молекула имеет симметрии, когда точки (x, y, z) и (−x, −y, −z) соответствуют одинаковым объектам. Например, если имеется атом кислорода в некоторой точке (x, y, z), то имеется атом кислорода и в точке (−x, −y, −z). В самом центре симметрии может находиться атом, а может там и не быть ничего. Примерами являются фторид ксенона, в котором центром является атом ксенона Xe, и бензол (), в котором центром является центр кольца.
- Зеркально-поворотная ось симметрии - ось, вокруг которой вращение на угол с последующим отражением относительно плоскости, перпендикулярной этой оси, оставляет молекулу неизменной, где n — порядок оси. Называется также несобственной n-кратной осью вращения и обозначается как . Примеры представлены в тетраэдральном тетрафториде кремния с тремя осями и Шаблон:Нп5Шаблон:R этана с одной осью . Ось соответствует плоскости отражения , а есть центральная инверсия i. Молекула, не имеющая осей для любого значения n является хиральной молекулой.
- Тождество -обозначаемое как E (от немецкого «Einheit», что означает единица, единство). Этот элемент симметрии просто состоит из отсутствия изменений. Каждая молекула имеет этот элемент. Хотя этот элемент выглядит физически тривиальным, он должен быть включён в список элементов симметрии, чтобы этот список образовывал группу, определение которой требует наличие такого элемента. Название «единица» проистекает по аналогии с умножением на единицу. Другими словами, E — это свойство, которое нужно любому объекту независимо от его свойств симметрии Шаблон:Sfn.
Операции

Пять элементов симметрии имеют ассоциированные с ними пять типов Шаблон:Нп5, которые оставляют молекулу в неразличимом от начального состоянии. Иногда для отличия элементов симметрии они помечаются значком «карет» или «циркумфлекс» (крышечка). Тогда — это вращение молекулы вокруг оси, а — операция тождественности. Элемент симметрии может иметь более одной операции симметрии, ассоциированной с ним. Например, ось Шаблон:Нп5 молекулы фторида ксенона () ассоциирована с двумя вращениями на 90° в противоположных направлениях и вращением на 180°. Поскольку эквивалентно , эквивалентна , а эквивалентна î, все операции симметрии могут быть разбиты на собственные и несобственные вращения.
Для линейных молекул вращение по часовой стрелке или против часовой стрелки вдоль оси молекулы на любой угол является операцией симметрии.
Группы симметрии
Группы
Операции симметрии молекулы (или другого объекта) образуют группу. В математике, группа — это множество с бинарной операцией, которая удовлетворяет четырём перечисленным ниже свойствам.
В группе симметрии элементами группы являются операции симметрии (не элементы симметрии) и бинарные комбинации состоят из применения одной операции, а затем другой. Примером служит последовательность вращения относительно оси z и отражения относительно плоскости xy, что обозначается . По соглашениям операции выполняются справа налево.
Группа симметрии обладает всеми свойствами групп.
- Свойство замкнутости:
- Для любой пары элементов x и y из G произведение x*y также находится в G.
- (в символьном виде, для любых двух элементов , ). Это означает, что группа замкнута, так что комбинирование пар элементов не даёт новых элементов. Операции симметрии обладают этим свойством, поскольку последовательность двух симметрий даёт третье состояние, неотличимое от второго, а потому от первого, так что в результате молекула остаётся результатом операции симметрии.
- Ассоциативность:
- Для любых x, y и z из G оба выражения и дают один и тот же элемент из G.
- (в символьном виде, для любых в символьном виде ).
- Свойство существования нейтрального элемента:
- Должен существовать элемент (скажем, e) из G, такой что умножение любого элемента из G на e не изменяет элемент.
- (в символьном виде, x*e=e*x= x для любого ).
- Существование обратного элемента:
- Для каждого элемента x из G должен существовать элемент y из G, такой что произведение x и y является нейтральным элементом e.
- (в символьном виде, для любого существует , такой что для любого ).
Порядок группы — это число элементов в группе. Для групп малого порядка свойства группы легко проверить рассмотрением таблицы композиций, в которой строки и столбцы соответствуют элементам группы, а ячейки таблицы соответствую их произведению.
Точечные группы и перестановочно-инверсионные группы

Последовательное применение (или композиция) одной или нескольких операций симметрии молекулы имеет эффект, эквивалентный применению одной отдельной операции симметрии. Например, вращение с последующим отражением рассматривается как операция симметрии . (Операция A с последующей операцией B с образованием операции C записывается как BA = C) Шаблон:Sfn. Более того, множество всех операций симметрии (включая составные операции) удовлетворяют всем свойствам группы, приведённым выше. Так что (S,*) является группой, где S — множество всех операций симметрии той же самой молекулы, а означает композицию (повторное применение) операций симметрии.
Эта группа называется точечной группой молекулы, поскольку множество операций симметрии оставляет по крайней мере одну точку фиксированной (хотя для некоторых симметрий остаётся фиксированной ось или плоскость). Другими словами, точечная группа — это группа, которая подытоживает все операции симметрии, которые имеют молекулы данной категорииШаблон:Sfn. Симметрия кристалла, в отличие от этого, описывается кристаллографической группой операций симметрии, которая включает параллельные переносы в пространстве.
Можно определить операции симметрии точечной группы для конкретной молекулы путём рассмотрения геометрической симметрии для молекулярной модели молекулы. Однако, если используется точечная группа для классификации состояний молекулы, операции в ней не интерпретируются тем же самым образом. Вместо этого операции интерпретируются как вращения и/или отражения электронно-колебательных координатШаблон:Sfn и эти операции коммутируют с колебательным гамильтонианом. Они являются «операциями симметрии» для этого гамильтониана. Точечная группа используется для классификации колебательных собственных состояний по симметрии. Классификация симметрии вращательных уровней, собственных состояний полного (вращательно-колебательно-электронного) гамильтониана требует использование подходящей перестановочно-инверсионной группы как у Лонге-ХиггинсаШаблон:Sfn.
Примеры точечных групп
Назначение каждой молекуле точечной группы классифицирует категории с похожими свойствами симметрии. Например, и имеют идентичные операции симметрииШаблон:Sfn. Все они могут подвергнуться тожественной операции E, двум операциям вращения и трём различным отражениям относительно плоскостей без потери идентичности, так что все они обладают одной и той же точечной группой порядка 6Шаблон:Sfn. Аналогично вода () и сероводород () также разделяют идентичные операции симметрии. Оба вещества могут подвергаться тождественной операции E, одному вращению и двум отражениям без потери идентичности, так что оба вещества обладают одной точечной группой порядка 4Шаблон:Sfn. Эта система классификации помогает учёным изучать молекулы более эффективно, поскольку химические молекулы с той же самой точечной группой обладают похожими схемами связей, имеют одинаковые диаграммы связей и спектральные свойстваШаблон:Sfn.
Точечные группы
Следующая таблица содержит многие из точечных групп, применимых к молекулам. Группы помечены с помощью символов Шёнфлиса, общеупотребительных в химии и молекулярной спектроскопии. Описания включают общие формы молекул, которые могут быть объяснены с помощью модели ОЭПВО. В каждой строке описания и примеры не имеют более высоких симметрий, что означает, что указанная точечная группа захватывает все точечные симметрии.
| Точечная группа | Операции симметрииШаблон:Sfn | Простое описание типичной геометрии | Пример 1 | Пример 2 | Пример 3 |
|---|---|---|---|---|---|
| C1 | E | Нет симметрии, хиральная |  Шаблон:Нп5 (показаны оба энантиомера) |
 Лизергиновая кислота |
 L-лейцин и большинство других -аминокислот, за исключением глицина |
| Cs | Плоскость отражения | 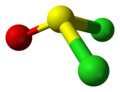 Тионилхлорид |
 Хлорноватистая кислота |
 Шаблон:Нп5 | |
| E i | Центр симметрии | 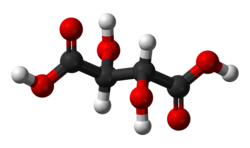 Мезовинная кислота |
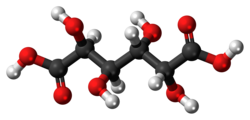 Слизевая кислота (мезогалактаровая кислота) |
(S,R) 1,2-дибромо-1,2-дихлорэтан (Шаблон:Нп5) | |
| Линейная |  Фтороводород (и все другие гетероядерые двухатомные молекулы) |
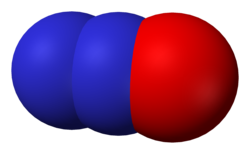 Оксид азота (закись азота) |
 Синильная кислота (цианистый водород) | ||
| Линейная с центром инверсии |  Кислород (и все другие гомоядерные двухатомные молекулы) |
 Диоксид углерода |
 Ацетилен (этин) | ||
| «Геометрия открытой книги», хиральная |  Пероксид водорода |
 Гидразин |
 Тетрагидрофуран (конформация «твист», скрученная конформация) | ||
| Пропеллер, хиральная |  Трифенилфосфин |
 Триэтиламин |
 Ортофосфорная кислота | ||
| Плоская с центром симметрии, нет вертикальной плоскости |  Транс-Шаблон:Нп5 |
 Транс-дифтордиазин |
 Транс-азобензол | ||
| Пропеллер | 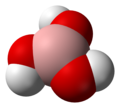 Борная кислота |
 Флороглюцин (1,3,5-тригидроксибензол) |
|||
| Угол (), качели () или в виде буквы T (ClF3) |  Монооксид водорода |
 Тетрафторид серы |
 Фторид хлора | ||
| Тригонально-пирамидальная |  Неинвертированный аммиак |
 Оксихлорид фосфора |
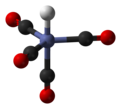 Тетракарбонилкобальтовая кислота, HCo(CO)4 | ||
| Квадратно пирамидальная |  Оксид-тетрафторид ксенона |
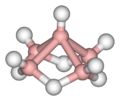 Пентаборан, B5H9 |
 Шаблон:Нп5 [Fe(CN)5(NO)]2− | ||
| Комплекс «табурет для доения» |  Циклопентадиенилникельнитрозил |
 Кораннулен |
|||
| Скрученная, хиральная |  Дифенил (скошенная конформация) |
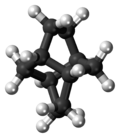 Твистан (C10H16) |
конформация циклогексана (твист) | ||
| Тройная спираль, хиральная | 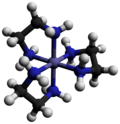 Шаблон:Нп5 Шаблон:Нп5
|
 Анион трис-оксалата железа (III)| | |||
| Плоская с центром симметрии, вертикальная плоскость |  Этилен |
 Пиразин |
 Диборан | ||
| Треугольная плоская или треугольная бипирамидальная | 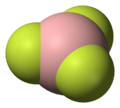 Трифторид бора |
 Хлоридфосфора (V) |
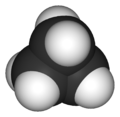 Циклопропан | ||
| Плоская квадратная |  Фторид ксенона (IV) |
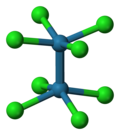 Шаблон:Нп5 |
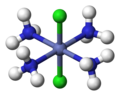 Транс — [CoIII(NH3)4Cl2]+ (исключая атомы водорода) | ||
| Пятиугольная | 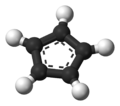 Шаблон:Нп5 |
 Рутеноцен |
 Фуллерен C70 | ||
| Шестиугольная |  Бензол |
 Шаблон:Нп5 |
 Коронен (C24H12) | ||
| Семиугольная |  Шаблон:Нп5 () cation |
||||
| Восьмиугольная | 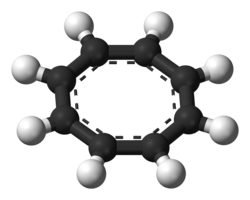 Анион циклооктатетраена () |
 Шаблон:Нп5 |
|||
| 90° поворот |  Аллен |
 Тетранитрид тетрасеры |
 Шаблон:Нп5 (возбуждённое состояние) | ||
| 60° поворот | 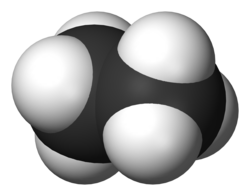 Этан (зигзагообразный Шаблон:Нп5) |
 Октакарбонилдикобальт (изомер без мостов) |
 Конформация циклогексана (кресло) | ||
| 45° поворот | 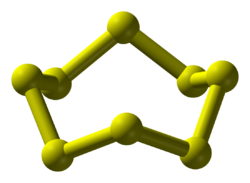 Шаблон:Нп5 (конформация «корона» ) |
 Шаблон:Нп5 (зигзагообразный поворотный изомер) |
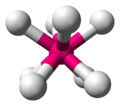 Шаблон:Нп5 (идеализированная геометрия) | ||
| 36° поворот | 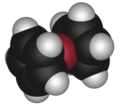 Ферроцен (зигзагообразный поворотный изомер) |
||||
 1,2,3,4 — тетрафторспиропентанШаблон:Sfn> |
|||||
| Тетраэдраэдральная |  Метан |
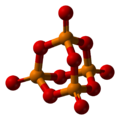 Оксид фосфора (V) |
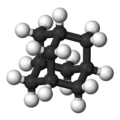 Адамантан | ||
| Икосаэдр с пиритоэдральной симметрией | Некоторые гексааддукты фуллерена C60[1] | ||||
| Октаэдральная или кубическая |  Фторид серы (VI) |
 Гексакарбонил молибдена |
 Кубан | ||
| Икосаэдральная или додекаэдральная |  Шаблон:Нп5 |
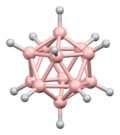 Шаблон:Нп5 |
 Додекаэдран |
Представления
Операции симметрии могут быть представлены многими способами. Обычно представляются матрицами. Для любого вектора, представляющего точку в декартовой системе координат умножение слева на матрицу даёт новое положение точки после операции симметрии. Композиция операций соответствует умножению матриц. В точечной группе умножение матриц двух симметрий приводит к матрице другой операции симметрии в той же точечной группеШаблон:Sfn. В примером служит
Хотя существует бесконечное число таких представлений, обычно используются неприводимые представления группы, поскольку все другие представления можно описать как линейную комбинацию неприводимых представлений.
Таблицы характеров
Для каждой точечной группы таблица характеров суммирует информацию об операциях симметрии и о её неприводимых представлениях. Поскольку всегда число неприводимых представления равно числу классов операций симметрии, таблицы квадратные.
Сама таблица состоит из характеров, которые представляют, каким образом конкретное неприводимое представление изменяется, если применить конкретную операцию симметрии. Любая операция симметрии в точечной группе молекулы, действуя на молекулу, оставляет молекулу неизменной. Но при действии на объект общего вида, такой как вектор или орбиталь, это не обязательно имеет место. Вектор может изменить направление, а орбиталь может изменить тип. Для простых точечных групп значения равны либо 1, либо −1. 1 означает, что знак или фаза (вектора или орбитали) не меняется операцией симметрии (симметричная операция), а −1 означает смену знака (асимметричная операция).
Представления маркируются согласно набору соглашений:
- A, если вращение вокруг главной оси симметрично;
- B, если вращение вокруг главной оси асимметрично;
- E и T являются дважды и трижды вырожденными представлениями соответственно;
- Если точечная группа имеет центр симметрии, индекс g (от Шаблон:Lang-de = чётный) сигнализирует отсутствие изменения в знаке, а индекс u (ungerade = нечётный) сигнализирует о смене знака;
- Для точечных групп и символы заимствованы из описания момента импульса: , , .
Таблицы также содержат информацию, как изменяются декартовы координатные вектора вращения вокруг них и квадратичные функции под действием операций симметрии группы путём указания, какое неприводимое представление действует тем же образом. Эти уточнения приведены в правых столбцах таблицы. Эта дополнительная информация полезна, поскольку химически важные орбитали (в частности орбитали p и d) имеют те же симметрии, что и эти структуры.
Таблица характеров для точечной группы симметрии дана ниже:
| 1 | 1 | 1 | 1 | z | ||
| 1 | 1 | −1 | −1 | xy | ||
| 1 | −1 | 1 | −1 | xz | ||
| 1 | −1 | −1 | 1 | yz |
Рассмотрим пример воды (), которая имеет описанную выше симметрию . Орбиталь кислорода имеет симметрию как в четвёртой строке таблицы характеров выше, с x в шестом столбце). Она расположена перпендикулярно плоскости молекулы и меняет знак при операциях и , но остаётся неизменной при остальных двух операциях (очевидно, что характер для тождественной операции всегда равен +1). Тогда набор характеров орбиталей есть {1, −1, 1, −1}, что соответствует неприводимому представлению . Аналогично, 2pz орбиталь имеет симметрию неприводимого представления (то есть ни одна из операций симметрии не меняет её), орбиталь имеет симметрию и орбиталь имеет симметрию .
Исторический обзор
Ханс Бете использовал характеры операций точечной группы при изучении Шаблон:Нп5 в 1929 году, а Юджин Вигнер использовал теорию групп для объяснения выбора правилатомной спектроскопииШаблон:Sfn. Первую таблицу характеров создал Ласло Тисса (1933) в связи с колебательными спектрами. Роберт Малликен первым опубликовал таблицы характеров на английском языке (1933), а Е. Брайт Уилсон использовал их в 1934 году для предсказания симметрии нормальных колебанийШаблон:Sfn. Полный набор 32 кристаллографических точечных групп опубликовали в 1936 году Розенталь и МёрфиШаблон:Sfn.
Молекулярная нежёсткость
Шаблон:См. также Как обсуждалось выше в разделе Точечные группы и перестановочно-инверсионные группы, точечные группы полезны для классификации колебательных состояний жёстких молекул (иногда называемых полужёсткими молекулами), которые претерпевают лишь малые колебания около равновесной геометрии. Лонге-Хиггинс ввели более общий тип группы симметрии, пригодный не только для классификации ровибронных состояний жёстких молекул, но также классификацию состояний нежёстких (или флуктуирующих) молекул, переходящих к эквивалентным геометриям (называемыми версиямиШаблон:Sfn), что может вызвать эффект искажения вращения молекулыШаблон:Sfn. Эти группы известны как перестановочно-инверсионные группы, поскольку операции симметрии в них являются энергетически возможными перестановками идентичных ядер, инверсией по отношению к центру массы (операция чётности), или комбинацией этих операций.
Например, этан () имеет три эквивалентные Шаблон:Нп5Шаблон:R. Переход между конформациями случается при обычных температурах путём внутреннего вращения метиловой группы относительно остальных составляющих. Это не вращение полной молекулы относительно оси . Хотя каждая конформация имеет симметрию , как в таблице выше, описание внутренних вращений и связанных квантовых состояний и уровней энергии требует более полной перестановочно-инверсионной группы .
Аналогично аммиак () имеет две пирамидальные () конформации, которые превращаются друг в друга в процессе, известном как Шаблон:Нп5. Это не операция инверсии точечной группы i в жёстких молекулах с центральной симметрией поскольку не имеет центра симметрии. Скорее это изменение ядра и электронных координат в центре масс молекулы (иногда называемой операцией чётности), что оказывается энергетически возможным для этой молекулы. Подходящая перестановочно-инверсионная группа, используемая в этой ситуации, это , которая изоморфна точечной группе .
Кроме того, в качестве примеров, метан () и молекулы имеют структуры симметричного равновесия с точечными группами симметрии и соответственно. В них отсутствуют постоянные электрические дипольные моменты, но они имеют очень слабые спектры вращения за счёт вращательного центробежного искаженияШаблон:SfnШаблон:Sfn. Перестановочно-инверсионные группы, требующиеся для полного изучения молекул и , это и соответственно.
Второй и менее общий подход к симметрии нежёстких молекул принадлежит АльтмануШаблон:SfnШаблон:Sfn. В этом подходе группы симметрии известны как супергруппы Шрёдингера и состоят из двух типов операций (и их комбинаций): (1) операции геометрической симметрии (вращение, отражение в плоскости, центральная симметрия) жёстких молекул и (2) изодинамические операции, которые переводят нежёсткие молекулы в энергетически эквивалентные формы путём физических процессов, таких как вращение одной связи (как в этане) или перестановки в молекуле (как в аммиаке) Шаблон:Sfn.
См. также
- Чётность (физика);
- Шаблон:Ссылка на раздел;
- Правило Вудворда — Хофмана;
- Шаблон:Нп5;
- Таблица характеров;
- Кристаллографическая точечная группа симметрии;
- Точечная группа в трёхмерном пространстве;
- Шаблон:Нп5;
- Симметрия в квантовой механике.
Примечания
Литература
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга
- Шаблон:Статья
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Книга
- Шаблон:Статья
- Шаблон:Статья
- Шаблон:Книга
- Шаблон:Книга
Ссылки
- Point group symmetry @ Newcastle University;
- Molecular symmetry @ Imperial College London;
- Molecular Point Group Symmetry Tables;
- Character tables for point groups for chemistry;
- Molecular Symmetry Online @ The Open University of Israel;
- Symmetry @ Otterbein;
- An internet lecture course on molecular symmetry @ Bergische Universitaet;
- DECOR — Symmetry @ The Cambridge Crystallographic Data Centre.